Why the value of Golden Ratio is 1.618 and how is it related to Binet’s formula ?
Last Updated :
01 Nov, 2022
Golden Ratio: Two numbers, say A and B are said to be in the golden ratio if their ratio equals the ratio of the sum of two numbers to the larger number, i.e.,
Suppose A > B, then
If A/B = (A + B)/A = ∅ = 1.618(Golden Ratio),
then these two numbers are said to be in golden ratio.
It is denoted by ∅ and its value is equal to 1.6180339…, which is an Irrational Number.
Binet’s Formula: This formula is used to find the Nth term in the Fibonacci Sequence which is given by:
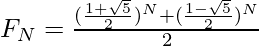
where, FN is the Nth term in the Fibonacci Sequence.
For the equation: (x2 – x – 1 = 0) Below are the relation that can be deduced:
=> x2 – x – 1 = 0
=> x2 = x + 1
=> x3 = x*x2 = x*(x+1) = x2 + x = 2x + 1
=> x4 = x*x3 = x*(2x+1) = 2x2 + x = 2(x+1) + x = 3x + 2
=> x5 = x*x4 = x*(3x+2) = 3x2 + 2x = 3(x+1) + 2x = 5x + 3
The next term for the next power of x can be guessed by looking at the above pattern. Observe that the coefficient of xN is equal to the sum of the coefficient of x(N – 1) and x(N – 2). The same pattern can be observed in the remaining term also. So, the next power of x can be directly expressed as:
=> x = x
=> x2 = x+1
=> x3 = 2x + 1
=> x4 = 3x + 2
=> x5 = 5x + 3
=> x6 = 8x + 5
=> x7 = 13x + 8
…
The Fibonacci Sequence is given by {0, 1, 1, 2, 3, 5, 8, 13, 21, …, }, and there exists a relation between the two, after observing the above two sequences. It can be said that:
xN = fNx + f(N – 1)
where, fN is the nth term in the Fibonacci sequence (n > 0).
Now, Let the roots of the equation: (x2 – x – 1 = 0) are ∝ and β, then
∝ = (1 + √5)/2
β = (1 – √5)/2
It can be said that:
=> ∝2 – ∝ – 1 = 0 and β2 – β – 1 = 0
=> ∝n = fn∝ + fn-1 and βn = fnβ + fn-1
=> ∝n – βn = fn(∝ – β)
=> fn = (∝n – βn) / (∝ – B)
After substituting the values of ∝ and β in the above equation:
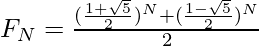
The above equation is known as Binet’s Formula. And the value (1+√5)/2 is known as the Golden Ratio, which is equal to 1.618. Therefore, the Nth Fibonacci Number is given by:
FN ≈ ∅N
where, where, ∅ is the Golden Ratio and Fn is the nth Fibonacci term.
Applications:
- Golden Ratio: It is used in architecture, paintings, photography and is also present in many forms in nature itself like in the Nautilus shell, sunflower, etc.
- Binet’s formula: It is used to find the Nth term in the Fibonacci sequence, which makes it really useful in Mathematics and many fields of computer science as well.
- Golden Ratio and Binet’s formula: They are also used in calculating the time complexities of algorithms like the Euclidean Algorithm etc.
Share your thoughts in the comments
Please Login to comment...