Deriving the expression of Fibonacci Numbers in terms of golden ratio
Last Updated :
12 Dec, 2018
Prerequisites: Generating Functions,
Fibonacci Numbers,
Methods to find Fibonacci numbers.
The method of using
Generating Functions to solve the famous and useful
Fibonacci Numbers‘ recurrence has been discussed in this post.
The
Generating Function is a powerful tool for solving a wide variety of mathematical problems, including counting problems. It is a formal power series. For example, in counting problems, we are often interested in finding the number of objects of size
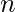
. In such a case, we define a power series, which, in simple terms is an infinite term polynomial where the coefficient of the
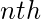
degree term is the
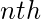
term of the sequence. This helps us to find many interesting and important results. It should be noted that in the use of generating functions, we generally use the coefficients in the generating function power series, we rarely use the variable in the series. In this post too, we shall do the same. The ordinary generating function of some a
n is:
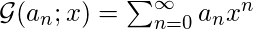
Fibonacci Numbers are one of the fundamental sequences in mathematics, and numerous ways have been discovered to find out the higher order terms of this sequence. This post discusses one such method.
Let’s first define a generating function for the Fibonacci Numbers, and then the function will be simplified to get a recurrence. Using this, expand the simplification and break it into partial fractions, and then use two standard power series, and later combine them both to arrive at surprising result for the
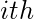
term of the Fibonacci Series.
Let us define the generating function
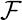
as
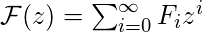
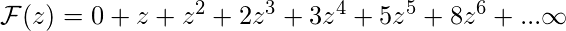 ,
where
,
where 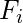 is the ith Fibonacci Number.
is the ith Fibonacci Number.
Since,
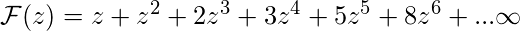
.
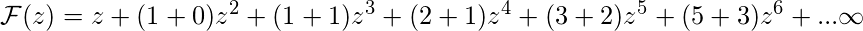
.
Rearranging them we get,
![Rendered by QuickLaTeX.com \mathcal{F}(z) = z + [z^2 + z^3 + 2z^4 + 3z^5 + 5z^6 + ... \infty] + [0 + z^3 + z^4 + 2z^5 + 3z^6 + ... \infty]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12fcad64c91296951a64ced9d8e8215c_l3.png)
.
Taking the common terms,
![Rendered by QuickLaTeX.com \mathcal{F}(z) = z + (z)[z + z^2 + 2z^3 + 3z^4 + 5z^5 + ... \infty]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2b83ae9f6ab3be2cff5d2e692dffdbf_l3.png)
![Rendered by QuickLaTeX.com + (z^2)[0 + z^1 + z^2 + z^3 + 3z^4 + ... \infty]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ad6477d39311dddaa5b0ca9fd607f7c8_l3.png)
Simplifying it further, the below function is obtained.
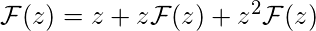
.
Solving for
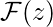
, we get:
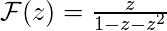
.
We get the below formula by above operations:
 ,
where,
,
where, 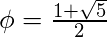 and
and 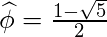 .
.
Thus,
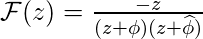
Also note that,
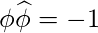
.
Thus, keeping this relation in above expression, we get,
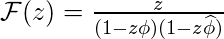
.
Now the right hand side of the above expression can be separated into partial fractions,
![Rendered by QuickLaTeX.com \mathcal{F}(z) = \frac{1}{\sqrt{5}}\left [ \frac{1}{(1-\phi z)} - \frac{1}{(1-\widehat{\phi} z)}\right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-399ddde8c421a3f0766584f1a31b9c05_l3.png)
.
Using
Expansion on the two fractions,
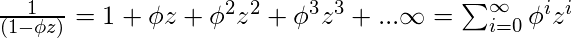
.
Similarly,
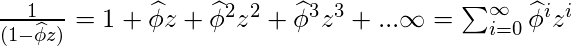
.
Thus,
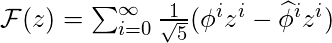
.
Thus,
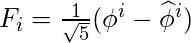
.
Now,

,
and,
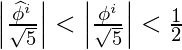
Using the above two facts, it can be safely concluded that the value of
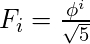 , rounded to the nearest integer.
, rounded to the nearest integer.
Finding n-th Fibonacci number using Golden ratio is one of the applications of this formula.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...