Types of Recursions
Last Updated :
07 Dec, 2022
What is Recursion?
The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function. Using recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.
Types of Recursions:
Recursion are mainly of two types depending on whether a function calls itself from within itself or more than one function call one another mutually. The first one is called direct recursion and another one is called indirect recursion. Thus, the two types of recursion are:
1. Direct Recursion: These can be further categorized into four types:
- Tail Recursion: If a recursive function calling itself and that recursive call is the last statement in the function then it’s known as Tail Recursion. After that call the recursive function performs nothing. The function has to process or perform any operation at the time of calling and it does nothing at returning time.
Example:
C++
#include <iostream>
using namespace std;
void fun(int n)
{
if (n > 0) {
cout << n << " ";
fun(n - 1);
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
C
#include <stdio.h>
void fun(int n)
{
if (n > 0) {
printf("%d ", n);
fun(n - 1);
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
Java
class GFG {
static void fun(int n)
{
if (n > 0)
{
System.out.print(n + " ");
fun(n - 1);
}
}
public static void main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Python3
def fun(n):
if (n > 0):
print(n, end=" ")
fun(n - 1)
x = 3
fun(x)
|
C#
using System;
class GFG
{
static void fun(int n)
{
if (n > 0)
{
Console.Write(n + " ");
fun(n - 1);
}
}
public static void Main(string[] args)
{
int x = 3;
fun(x);
}
}
|
Javascript
<script>
function fun(n)
{
if (n > 0)
{
document.write(n + " ");
fun(n - 1);
}
}
var x = 3;
fun(x);
</script>
|
Let’s understand the example by tracing tree of recursive function. That is how the calls are made and how the outputs are produced.
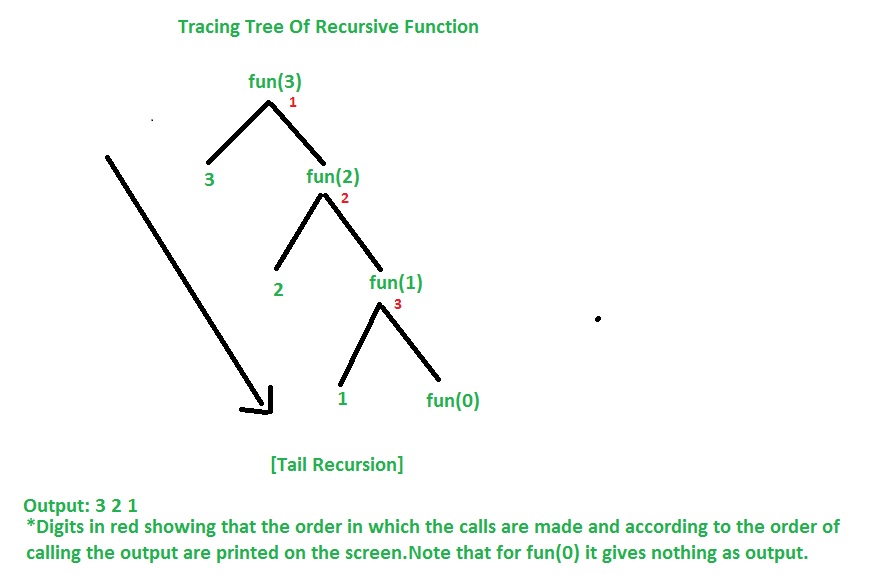
Time Complexity For Tail Recursion : O(n)
Space Complexity For Tail Recursion : O(n)
Note: Time & Space Complexity is given for this specific example. It may vary for another example.
Let’s now converting Tail Recursion into Loop and compare each other in terms of Time & Space Complexity and decide which is more efficient.
C++
#include <iostream>
using namespace std;
void fun(int y)
{
while (y > 0) {
cout << y << " ";
y--;
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
C
#include <stdio.h>
void fun(int y)
{
while (y > 0) {
printf("%d ", y);
y--;
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void fun(int y)
{
while (y > 0) {
System.out.print(" "+ y);
y--;
}
}
public static void main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Python3
def fun(y):
while (y > 0):
print(y , end = " ")
y -= 1
x = 3
fun(x)
|
C#
using System;
class GFG
{
static void fun(int y)
{
while (y > 0) {
Console.Write(" "+ y);
y--;
}
}
public static void Main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Javascript
<script>
function fun(y)
{
while (y > 0) {
document.write(" "+ y);
y--;
}
}
var x = 3;
fun(x);
</script>
|
Time Complexity: O(n)
Space Complexity: O(1)
Note: Time & Space Complexity is given for this specific example. It may vary for another example.
So it was seen that in case of loop the Space Complexity is O(1) so it was better to write code in loop instead of tail recursion in terms of Space Complexity which is more efficient than tail recursion.
Why space complexity is less in case of loop ?
Before explaining this I am assuming that you are familiar with the knowledge that’s how the data stored in main memory during execution of a program. In brief,when the program executes,the main memory divided into three parts. One part for code section, the second one is heap memory and another one is stack memory. Remember that the program can directly access only the stack memory, it can’t directly access the heap memory so we need the help of pointer to access the heap memory.
Let’s now understand why space complexity is less in case of loop ?
In case of loop when function “(void fun(int y))” executes there only one activation record created in stack memory(activation record created for only ‘y’ variable) so it takes only ‘one’ unit of memory inside stack so it’s space complexity is O(1) but in case of recursive function every time it calls itself for each call a separate activation record created in stack.So if there’s ‘n’ no of call then it takes ‘n’ unit of memory inside stack so it’s space complexity is O(n).
- Head Recursion: If a recursive function calling itself and that recursive call is the first statement in the function then it’s known as Head Recursion. There’s no statement, no operation before the call. The function doesn’t have to process or perform any operation at the time of calling and all operations are done at returning time.
Example:
C++
#include <bits/stdc++.h>
using namespace std;
void fun(int n)
{
if (n > 0) {
fun(n - 1);
cout << " "<< n;
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
C
#include <stdio.h>
void fun(int n)
{
if (n > 0) {
fun(n - 1);
printf("%d ", n);
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
Java
import java.io.*;
class GFG{
static void fun(int n)
{
if (n > 0) {
fun(n - 1);
System.out.print(" "+ n);
}
}
public static void main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Python3
def fun(n):
if (n > 0):
fun(n - 1)
print(n,end=" ")
x = 3
fun(x)
|
C#
using System;
class GFG{
static void fun(int n)
{
if (n > 0) {
fun(n - 1);
Console.Write(" "+ n);
}
}
public static void Main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Javascript
<script>
function fun(n)
{
if (n > 0) {
fun(n - 1);
document.write(" "+ n);
}
}
var x = 3;
fun(x);
</script>
|
Let’s understand the example by tracing tree of recursive function. That is how the calls are made and how the outputs are produced.
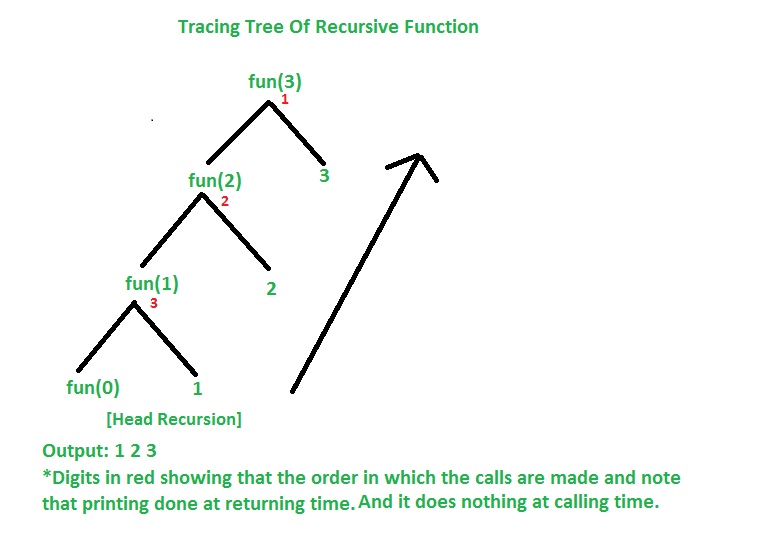
Time Complexity For Head Recursion: O(n)
Space Complexity For Head Recursion: O(n)
Note: Time & Space Complexity is given for this specific example. It may vary for another example.
Note: Head recursion can’t easily convert into loop as Tail Recursion but it can. Let’s convert the above code into the loop.
C++
#include <iostream>
using namespace std;
void fun(int n)
{
int i = 1;
while (i <= n) {
cout <<" "<< i;
i++;
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
C
#include <stdio.h>
void fun(int n)
{
int i = 1;
while (i <= n) {
printf("%d ", i);
i++;
}
}
int main()
{
int x = 3;
fun(x);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void fun(int n)
{
int i = 1;
while (i <= n) {
System.out.print(" "+ i);
i++;
}
}
public static void main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Python3
def fun(n):
i = 1
while (i <= n):
print(i,end=" ")
i+=1
x = 3
fun(x)
|
C#
using System;
class GFG
{
static void fun(int n)
{
int i = 1;
while (i <= n) {
Console.Write(" "+ i);
i++;
}
}
public static void Main(String[] args)
{
int x = 3;
fun(x);
}
}
|
Javascript
<script>
function fun(n)
{
var i = 1;
while (i <= n) {
document.write(" "+ i);
i++;
}
}
var x = 3;
fun(x);
</script>
|
- Tree Recursion: To understand Tree Recursion let’s first understand Linear Recursion. If a recursive function calling itself for one time then it’s known as Linear Recursion. Otherwise if a recursive function calling itself for more than one time then it’s known as Tree Recursion.
Example:
Pseudo Code for linear recursion
fun(n)
{
// some code
if(n>0)
{
fun(n-1); // Calling itself only once
}
// some code
}
Program for tree recursion
C++
#include <iostream>
using namespace std;
void fun(int n)
{
if (n > 0)
{
cout << " " << n;
fun(n - 1);
fun(n - 1);
}
}
int main()
{
fun(3);
return 0;
}
|
C
#include <stdio.h>
void fun(int n)
{
if (n > 0) {
printf("%d ", n);
fun(n - 1);
fun(n - 1);
}
}
int main()
{
fun(3);
return 0;
}
|
Java
class GFG
{
static void fun(int n)
{
if (n > 0) {
System.out.print(" "+ n);
fun(n - 1);
fun(n - 1);
}
}
public static void main(String[] args)
{
fun(3);
}
}
|
Python3
def fun(n):
if (n > 0):
print(n, end=" ")
fun(n - 1)
fun(n - 1)
fun(3)
|
C#
using System;
class GFG
{
static void fun(int n)
{
if (n > 0) {
Console.Write(" "+ n);
fun(n - 1);
fun(n - 1);
}
}
public static void Main(String[] args)
{
fun(3);
}
}
|
Javascript
<script>
function fun(n)
{
if (n > 0) {
document.write(" "+ n);
fun(n - 1);
fun(n - 1);
}
}
fun(3);
</script>
|
Let’s understand the example by tracing tree of recursive function. That is how the calls are made and how the outputs are produced.
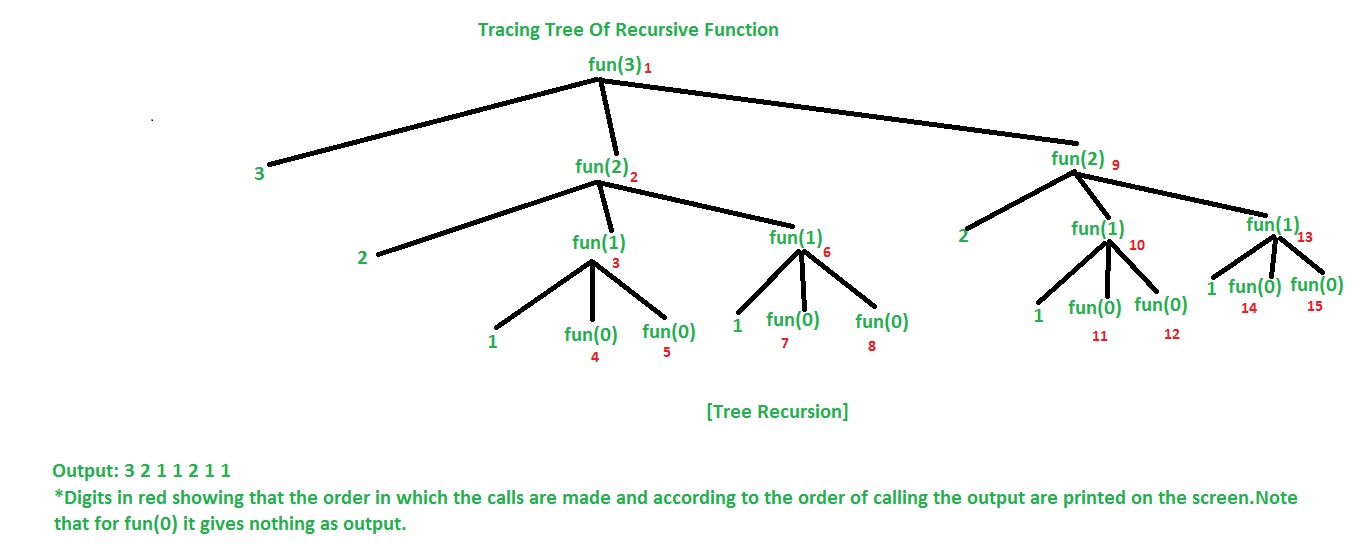
Time Complexity For Tree Recursion: O(2^n)
Space Complexity For Tree Recursion: O(n)
Note: Time & Space Complexity is given for this specific example. It may vary for another example.
- Nested Recursion: In this recursion, a recursive function will pass the parameter as a recursive call. That means “recursion inside recursion”. Let see the example to understand this recursion.
Example:
C++
#include <iostream>
using namespace std;
int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
int main()
{
int r;
r = fun(95);
cout << " " << r;
return 0;
}
|
C
#include <stdio.h>
int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
int main()
{
int r;
r = fun(95);
printf("%d\n", r);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
public static void main(String args[])
{
int r;
r = fun(95);
System.out.print(" "+ r);
}
}
|
Python3
def fun(n):
if (n > 100):
return n - 10
return fun(fun(n + 11))
r = fun(95)
print("", r)
|
C#
using System;
class GFG {
static int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
public static void Main(String []args)
{
int r;
r = fun(95);
Console.Write(" "+ r);
}
}
|
Javascript
<script>
function fun( n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
var r;
r = fun(95);
document.write(" "+ r);
</script>
|
Let’s understand the example by tracing tree of recursive function. That is how the calls are made and how the outputs are produced.

2. Indirect Recursion: In this recursion, there may be more than one functions and they are calling one another in a circular manner.
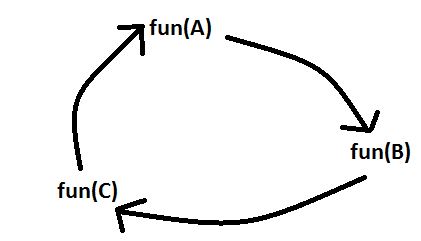
From the above diagram fun(A) is calling for fun(B), fun(B) is calling for fun(C) and fun(C) is calling for fun(A) and thus it makes a cycle.
Example:
C++
#include <iostream>
using namespace std;
void funB(int n);
void funA(int n)
{
if (n > 0) {
cout <<" "<< n;
funB(n - 1);
}
}
void funB(int n)
{
if (n > 1) {
cout <<" "<< n;
funA(n / 2);
}
}
int main()
{
funA(20);
return 0;
}
|
C
Java
import java.io.*;
class GFG{
static void funA(int n)
{
if (n > 0) {
System.out.print(" " +n);
funB(n - 1);
}
}
static void funB(int n)
{
if (n > 1) {
System.out.print(" " +n);
funA(n / 2);
}
}
public static void main (String[] args)
{
funA(20);
}
}
|
C#
using System;
class GFG{
static void funA(int n)
{
if (n > 0) {
Console.Write(" " +n);
funB(n - 1);
}
}
static void funB(int n)
{
if (n > 1) {
Console.Write(" " +n);
funA(n / 2);
}
}
public static void Main (String[] args)
{
funA(20);
}
}
|
Python3
def funA(n):
if (n > 0):
print("", n, end='')
funB(n - 1)
def funB( n):
if (n > 1):
print("", n, end='')
funA(n // 2)
funA(20)
|
Javascript
<script>
function funA(n)
{
if (n > 0) {
document.write(n.toFixed(0) + "</br>");
funB(n - 1);
}
}
function funB(n)
{
if (n > 1) {
document.write(n.toFixed(0) + "</br>");
funA(n / 2);
}
}
funA(20);
</script>
|
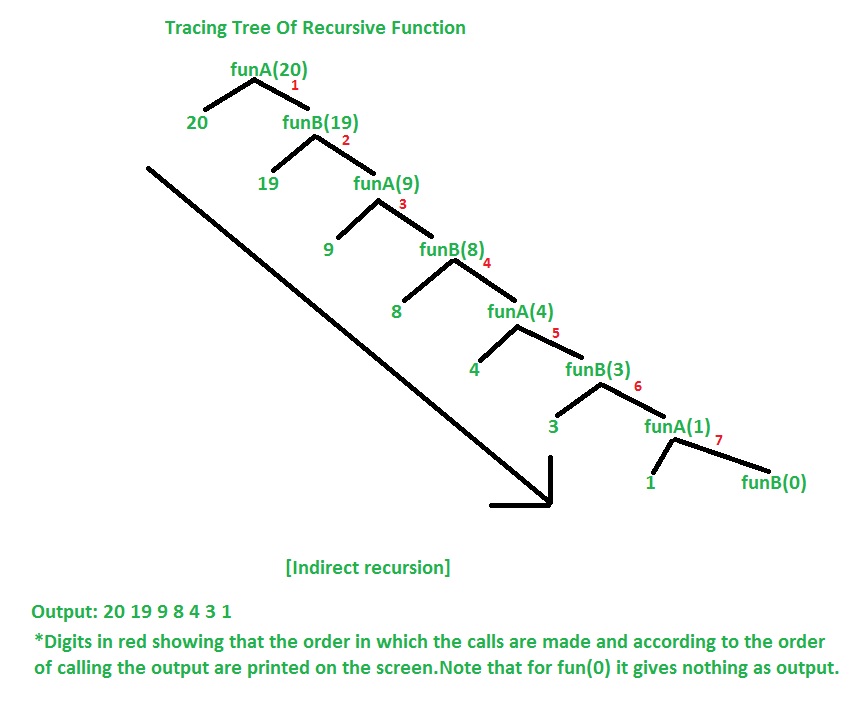
Let’s understand the example by tracing tree of recursive function. That is how the calls are made and how the outputs are produced.
Share your thoughts in the comments
Please Login to comment...