Mathematics | Total number of possible functions

In this article, we are discussing how to find number of functions from one set to another. For understanding the basics of functions, you can refer this: Classes (Injective, surjective, Bijective) of Functions. 

Number of functions from one set to another: Let X and Y are two sets having m and n elements respectively. In a function from X to Y, every element of X must be mapped to an element of Y. Therefore, each element of X has ‘n’ elements to be chosen from. Therefore, total number of functions will be n×n×n.. m times = n^m. 
For example: X = {a, b, c} and Y = {4, 5}. A function from X to Y can be represented in Figure 1. 

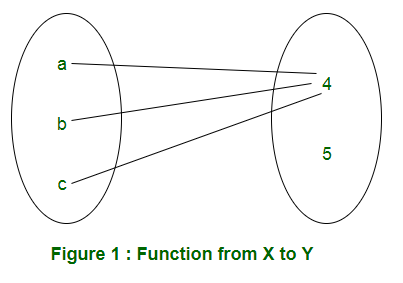
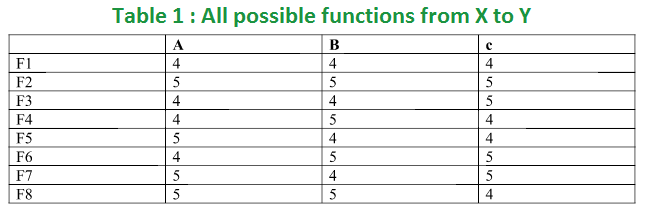
Considering all possibilities of mapping elements of X to elements of Y, the set of functions can be represented in Table 1. 

Examples: Let us discuss gate questions based on this: 

• Q1. Let X, Y, Z be sets of sizes x, y and z respectively. Let W = X x Y. Let E be the set of all subsets of W. The number of functions from Z to E is: 
  (A) z^2xy
  (B) z x 2^xy
  (C) z^{2x + y}
  (D) 2^xyz

  Solution: As W = X x Y is given, number of elements in W is xy. As E is the set of all subsets of W, number of elements in E is 2^xy. The number of functions from Z (set of z elements) to E (set of 2^xy elements) is 2^xyz. So the correct option is (D) 
  

• Q2. Let S denote the set of all functions f: {0,1}⁴ → {0,1}. Denote by N the number of functions from S to the set {0,1}. The value of Log2Log2N is ______. 
  (A) 12 
  (B) 13 
  (C) 15 
  (D) 16 

  Solution: As given in the question, S denotes the set of all functions f: {0, 1}⁴ → {0, 1}. The number of functions from {0,1}⁴ (16 elements) to {0, 1} (2 elements) are 2¹⁶. Therefore, S has 2¹⁶ elements. Also, given, N denotes the number of function from S(2¹⁶ elements) to {0, 1}(2 elements). Therefore, N has 2²¹⁶ elements. Calculating required value, 

  Log2(Log2 (2²¹⁶)) =Log2¹⁶ = 16 

  Therefore, correct option is (D). 
  

Number of onto functions from one set to another – In onto function from X to Y, all the elements of Y must be used. In the example of functions from X = {a, b, c} to Y = {4, 5}, F1 and F2 given in Table 1 are not onto. In F1, element 5 of set Y is unused and element 4 is unused in function F2. So, total numbers of onto functions from X to Y are 6 (F3 to F8). 

• If X has m elements and Y has 2 elements, the number of onto functions will be 2^m-2. 

  Explanation: From a set of m elements to a set of 2 elements, the total number of functions is 2^m. Out of these functions, 2 functions are not onto (If all elements are mapped to 1^st element of Y or all elements are mapped to 2^nd element of Y). So, number of onto functions is 2^m-2.

• If X has m elements and Y has n elements, the number if onto functions are, 
  
  

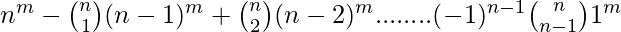
Important notes –

• The formula works only if m ≥ n.
• If m < n, the number of onto functions is 0 as it is not possible to use all elements of Y.

Q3. The number of onto functions (surjective functions) from set X = {1, 2, 3, 4} to set Y = {a, b, c} is: 
(A) 36 
(B) 64 
(C) 81 
(D) 72 

Solution: Using m = 4 and n = 3, the number of onto functions is: 
3⁴ – ³C₁(2)⁴ + ³C₂1⁴ = 36.