Mathematics | Classes (Injective, surjective, Bijective) of Functions
Last Updated :
04 Apr, 2019
A function f from A to B is an assignment of exactly one element of B to each element of A (A and B are non-empty sets). A is called Domain of f and B is called co-domain of f. If b is the unique element of B assigned by the function f to the element a of A, it is written as f(a) = b. f maps A to B. means f is a function from A to B, it is written as
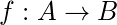 Terms related to functions:
Terms related to functions:
- Domain and co-domain – if f is a function from set A to set B, then A is called Domain and B is called co-domain.
- Range – Range of f is the set of all images of elements of A. Basically Range is subset of co- domain.
- Image and Pre-Image – b is the image of a and a is the pre-image of b if f(a) = b.
Properties of Function:
- Addition and multiplication: let f1 and f2 are two functions from A to B, then f1 + f2 and f1.f2 are defined as-:
f1+f2(x) = f1(x) + f2(x). (addition)
f1f2(x) = f1(x) f2(x). (multiplication)
- Equality: Two functions are equal only when they have same domain, same co-domain and same mapping elements from domain to co-domain.
Types of functions:
- One to one function(Injective): A function is called one to one if for all elements a and b in A, if f(a) = f(b),then it must be the case that a = b. It never maps distinct elements of its domain to the same element of its co-domain.
 We can express that f is one-to-one using quantifiers as
We can express that f is one-to-one using quantifiers as 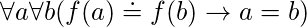 or equivalently
or equivalently 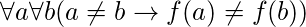 , where the universe of discourse is the domain of the function.
, where the universe of discourse is the domain of the function.
- Onto Function (surjective): If every element b in B has a corresponding element a in A such that f(a) = b. It is not required that a is unique; The function f may map one or more elements of A to the same element of B.

- One to one correspondence function(Bijective/Invertible): A function is Bijective function if it is both one to one and onto function.
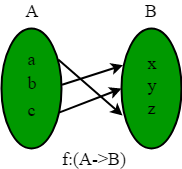
- Inverse Functions:Bijection function are also known as invertible function because they have inverse function property. The inverse of bijection f is denoted as f-1. It is a function which assigns to b, a unique element a such that f(a) = b. hence f-1 (b) = a.
Some Useful functions -:
Strictly Increasing and Strictly decreasing functions: A function f is strictly increasing if f(x) > f(y) when x>y. A function f is strictly decreasing if f(x) < f(y) when x<y.
Increasing and decreasing functions: A function f is increasing if f(x) ≥ f(y) when x>y. A function f is decreasing if f(x) ≤ f(y) when x<y.
Function Composition: let g be a function from B to C and f be a function from A to B, the composition of f and g, which is denoted as fog(a)= f(g(a)).
Properties of function composition:
- fog ≠ gof
- f-1 of = f-1 (f(a)) = f-1(b) = a.
- fof-1 = f(f-1 (b)) = f(a) = b.
- If f and g both are one to one function, then fog is also one to one.
- If f and g both are onto function, then fog is also onto.
- If f and fog both are one to one function, then g is also one to one.
- If f and fog are onto, then it is not necessary that g is also onto.
- (fog)-1 = g-1 o f-1
Some Important Points:
- A function is one to one if it is either strictly increasing or strictly decreasing.
- one to one function never assigns the same value to two different domain elements.
- For onto function, range and co-domain are equal.
- If a function f is not bijective, inverse function of f cannot be defined.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...