TCS Coding Practice Question | LCM of 2 Numbers
Last Updated :
11 Jan, 2023
Given two numbers, the task is to find the LCM of two numbers using Command Line Arguments. LCM (Least Common Multiple) of two numbers is the smallest number which can be divided by both numbers. For example, LCM of 15 and 20 is 60 and LCM of 5 and 7 is 35.  Examples:
Examples:
Input: n1 = 10, n2 = 15
Output: 30
Input: n1 = 5, n2 = 10
Output: 10
Approach:
- Since the numbers are entered as Command line Arguments, there is no need for a dedicated input line
- Extract the input numbers from the command line argument
- This extracted numbers will be in string type.
- Convert these numbers into integer type and store it in variables, say num1 and num2
- Find the LCM of the numbers. An efficient solution is based on the below formula for LCM of two numbers ‘a’ and ‘b’.
a x b = LCM(a, b) * GCD (a, b)
LCM(a, b) = (a x b) / GCD(a, b)
- To find the GCD or HCF, an efficient solution is to use Euclidean algorithm, which is the main algorithm used for this purpose. The idea is, GCD of two numbers doesn’t change if a smaller number is subtracted from a bigger number.
- Print or return the LCM
Program:
C
#include <stdio.h>
#include <stdlib.h> /* atoi */
int GCD(int a, int b)
{
if (b == 0)
return a;
return GCD(b, a % b);
}
int LCM(int a, int b)
{
return (a * b) / GCD(a, b);
}
int main(int argc, char* argv[])
{
int num1, num2;
if (argc == 1)
printf("No command line arguments found.\n");
else {
num1 = atoi(argv[1]);
num2 = atoi(argv[2]);
printf("%d\n", LCM(num1, num2));
}
return 0;
}
|
Java
class GFG {
static int GCD(int a, int b)
{
if (b == 0)
return a;
return GCD(b, a % b);
}
static int LCM(int a, int b)
{
return (a * b) / GCD(a, b);
}
public static void main(String[] args)
{
if (args.length > 0) {
int num1 = Integer.parseInt(args[0]);
int num2 = Integer.parseInt(args[1]);
int res = LCM(num1, num2);
System.out.println(res);
}
else
System.out.println("No command line "
+ "arguments found.");
}
}
|
Output:
- In C:

- In Java:
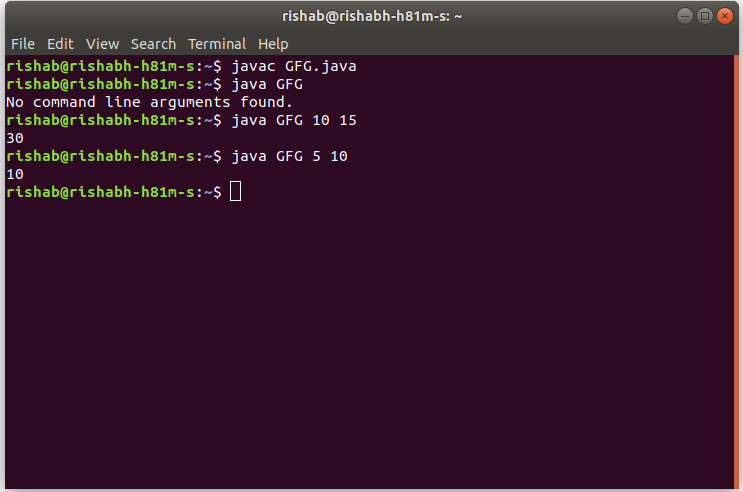
Time Complexity : O(logN)
Auxiliary Space: O(logN)
Share your thoughts in the comments
Please Login to comment...