TCS Coding Practice Question | Checking Prime Number

Given a number N, the task is to check if N is a Prime Number or not using Command Line Arguments.
Examples:

Input: N = 7
Output: Yes

Input: N = 15
Output: No

Approach:

• Since the number is entered as Command line Argument, there is no need for a dedicated input line
• Extract the input number from the command line argument
• This extracted number will be in String type.
• Convert this number into integer type and store it in a variable, say N
• Now loop through the numbers from 2 to N/2+1, using a variable say i. 
  In each iteration, 
  • Check if i divide N completely (i.e. if it is a factor of N).
  • If yes, then N is not a prime number.
  • If no, then N is a prime number.
• After the loop has ended, it is found out that N is prime or not.

Note: Please note that 1 is not checked in this scenarios because 1 is neither prime nor composite.
Program:

C

// C program to find
// the Prime Numbers from 1 to N
// using command line arguments

#include <stdio.h>

#include <stdlib.h> /* atoi */

// Function to check if x is prime
int isPrime(int x)
{
    int i;

    // Loop to check if x has any factor
    // other than 1 and x itself
    for (i = 2; i < x / 2 + 1; i++) {
        if (x % i == 0) {
            // Since i is a factor of x
            // x is not prime
            return 0;
        }
    }

    // x is prime
    return 1;
}

// Driver code
int main(int argc, char* argv[])
{

    int n;

    // Check if the length of args array is 1
    if (argc == 1)
        printf("No command line arguments found.\n");
    else {

        // Get the command line argument and
        // Convert it from string type to integer type
        // using function "atoi( argument)"
        n = atoi(argv[1]);

        // Check if n is prime
        if (isPrime(n) == 1)
            printf("Yes\n");
        else
            printf("No\n");
    }

    return 0;
}

Java

// Java program to reverse a string
// using command line arguments

class GFG {

    // Function to check if x is prime
    public static int isPrime(int x)
    {
        int i;

        // Loop to check if x has any factor
        // other than 1 and x itself
        for (i = 2; i < x / 2 + 1; i++) {
            if (x % i == 0) {
                // Since i is a factor of x
                // x is not prime
                return 0;
            }
        }

        // x is prime
        return 1;
    }

    // Driver code
    public static void main(String[] args)
    {

        // Check if length of args array is
        // greater than 0
        if (args.length > 0) {

            // Get the command line argument and
            // Convert it from string type to integer type
            int n = Integer.parseInt(args[0]);

            // Check if n is prime
            if (isPrime(n) == 1)
                System.out.println("Yes");
            else
                System.out.println("No");
        }
        else
            System.out.println("No command line "
                               + "arguments found.");
    }
}

Python3

import sys

# checking prime or not
def is_prime(number):
    if number <= 1:
        return False

    sqrt_number = int(number ** 0.5)

    # Loop to check if number has any factor
    # other than 1 and number itself

    for i in range(2, sqrt_number + 1):
        # Since i is a factor of number
        # number is not prime
        if number % i == 0:
            return False

    return True

if __name__ == "__main__":

    # Check if length of argv is not equal to 2
    if len(sys.argv) != 2:
        print("Usage: python prime_check.py <number>")
        sys.exit(1)

    # Get the command line argument and
    # Convert it from string type to integer type
    # using function "int(sys.argv[1])"
    number = int(sys.argv[1])

    if is_prime(number):
        print(number, "is prime.")
    else:
        print(number, "is not prime.")

#puligokulakishorereddy

Output:

• In C: 

• In Java:

• In Python

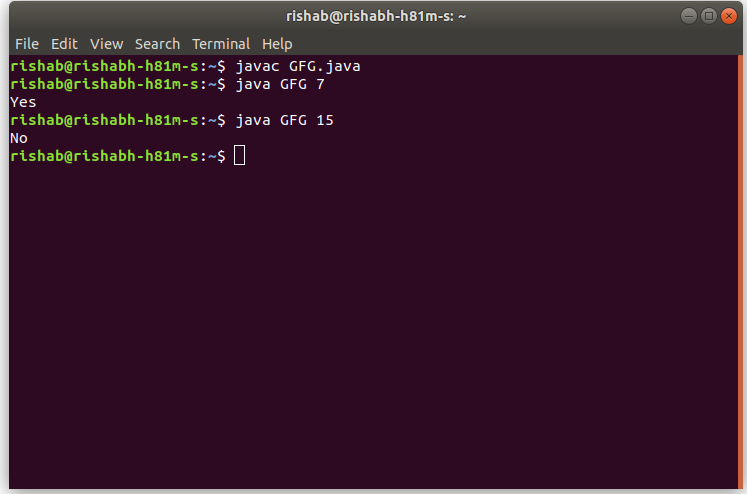
Time Complexity: O(N)
Auxiliary Space: O(1)