Subsets in maths are a core concept in the study of Set Theory, similar to Sets. A group of elements, objects, or members enclosed in curly braces, such as {x, y, z} is called a Set, where each member of the set is unique. So for a set of {x, y, z} the possible subsets are {}, {x}, {y}, {z}, {x, y}, {y, z}, {z, x} or {x, y, z}. While defining a set its elements could be real numbers, constants, variables, or any other objects as well.
This article explores the concept of Subsets in detail and makes it easy to grasp for all the readers of the article without any regard to their academic level. All subtopics such as their meaning, definition, symbol, example, and many many more, are covered in the article with plenty of examples. So, let’s start our journey to the land of set theory and understand this concept of Subsets.
In this article, we have provided detailed information about what are subsets in maths, supersets in maths, proper subset, and improper subset with examples and FAQs.
What are Subsets in Maths?
A set ‘A’ is a subset of set ‘B’ if all the elements of set A come under set B. Also, a subset can be equal to a set in a particular case when all the elements of a subset are contained in the set.
In order to better understand a subset let’s consider a set A is a collection of odd numbers and set B consists of {1,3,5}, so here B is a subset of A and A is a superset of B.

For Example: If set A contains {apple, banana} and set B contains {all fruits} then A is the subset of B.
Let’s consider one more example for better understanding.
Example: Determine which is subset and which is superset, if A = {a, e, i, o, u} and B = { All alphabets}.
Answer:
Here A contains all vowels elements which are the part of alphabets. So Here A is subset of B and B is superset of A.
Subset Definition
Mathematically a Set A is supposed to be a subset of Set B if all the components of Set A are also existing in Set B. So, subset is a subgroup of any set. Set A is, in other words, contained within Set B.
For Example: If Set A = {1, 2, 3} and Set B = {1, 2, 3, 4, 5, 6} then we can say that Set A is a subset of Set B as all the elements in set A are available in set B.
Subset Meaning
A set whose elements are all elements of an inclusive set is the meaning of subset. Consider a set X such that X comprises the names of all the rivers of a country. Another set Y includes the names of rivers in your North India. Here y will be a subset of x because all the rivers in North India would also be rivers of our country; hence, Y is a subset of X. There are only a definite number of distinct or unique subsets for any set, therefore the remaining are irrelevant and repetitive.
Example: List all the subsets the set Q = {1, 2, 3}.
Answer:
The subsets of Q are { }, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3} and {1, 2, 3}
Subset Symbol
A subset is indicated by the symbol and read as ‘is a subset of’ in set theory. A subset is represented by a symbol given by ⊆. Subsets can be expressed using this symbol as follows:
“A ⊆ B” this signifies that Set A is a subset of Set B.
Example of Subsets
The only need for a set A to be a subset of a set B is that every element of A be present in B. Here are some instances of subsets based on this.
- A = {2, 3, 10} is a subset of B = {1, 2, 3, 4, 10},
- P = Set of All Prime Numbers is a subset of N = Set of All Natural Numbers, and
- X = {a, e, i, o ,u} are collection of vowels and is a subset of Y = Set of all Alphabets .
It is worth noting that every set is a subset of itself, as is the empty set ().
Example: Can null Set be a subset of any set?
Answer:
Null is subset of every set. By default we consider this fact that all set contain an element called null set.
Subsets of Real Number
Real numbers that can be expressed as decimal numbers fall into a variety of categories. From your daily existence, you are undoubtedly already familiar with fractions, decimals, and counting numbers. The following numbers are considered as subset of real numbers:
- Rational Numbers: Any number that can be expressed as a fraction, p/q, where p and q are both positive integers. These are non-terminating, repeating decimals and terminating decimals in decimal form. Ex: -5/9, 1/8
- Irrational Numbers: These numbers don’t end or repeat when expressed in decimal form. Ex: e.
- Integers: All counting numbers, including zero and their opposites. Ex: -2,-1,0,3
- Whole Numbers: Zero and all positive counting numbers. Ex- 0, 2, 500
- Natural Numbers: All positive counting numbers. Ex- 1,2,40
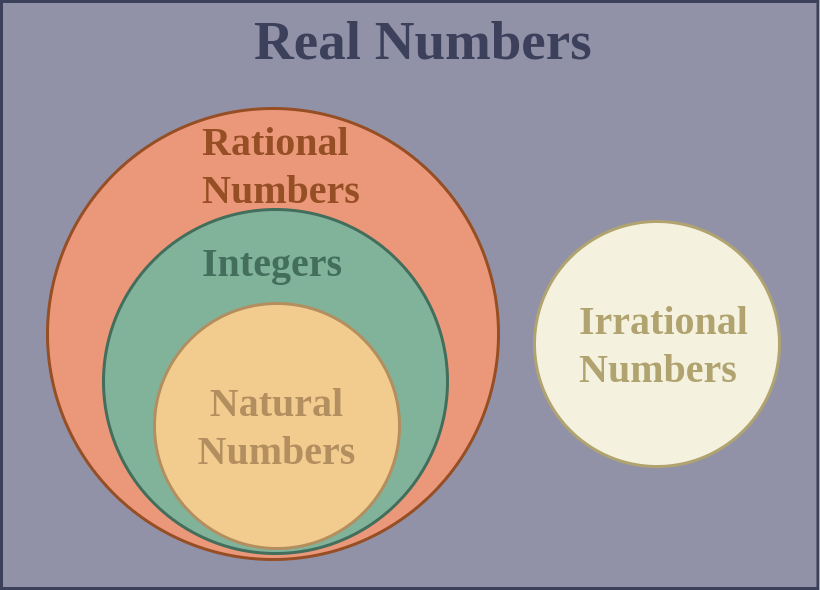
Example: To which subsets of the real numbers does -5 belong?
Answer:
-5 is a rational number and an integer.
Power Set of a Set
A set’s power set consists of every subset as well as the original set and the empty set. P(A) stands for the power set of a given set A. For example, If A = {1, 2}, then P(A) = {{ }, {1}, {2}, {1, 2}}. Here we can clearly see that all the subsets of A are contained in the P(A) i.e., power set of A.
Number of Subsets of a Set
For any set A, number of seusets are given using the following formula
Number of Subsets = 2n
Where n is number of elements in the set.
As power set contain all the subsets of any set, thus for a set A which has ‘n’ elements then P(A) has 2n elements.
Example: How many elements of power set can be formed if there are four elements in a set?
Answer:
Number of elements of power set with three elements are 24 = 16.
Types of Subsets
There are two types of subsets that are:
- Proper Subset
- Improper Subset
Let’s discuss these types in detail as follows:
Proper Subset
A proper subsetonly comprises a few members of the original set. Proper subset can never be equal to the original set. In proper subset the subset forming the original set is excluded.
Proper Subset Symbol
A proper subset is denoted by ⊂,
We can express a proper subset for set A and set B as;
A ⊂ B
Example of Proper Subsets
Let set A = {1, 3, 5}, then proper subsets of A are {}, {1}, {3}, {5}, {1, 3} {3, 5} {1, 5}. Also, {1, 3, 5} is a subset of A but it is not a proper subset of A.
Proper Subset Formula
The number of proper subsets of a set with ‘n’ elements is 2n – 1.
Example: A set contain 3 elements, what will be the number of proper subsets?
Answer:
Number of proper subsets = 2n – 1
Here, n = 3
N = 23 – 1 = 7
Improper Subset
An improper subset contains includes both the null set and each member of the initial set. Improper subset can be equal to the original set. In improper subset the subset forming the original set is included. This is represented by the symbol ⊆.
Example: What will be the improper subset of set A = {1, 3, 5}?
Answer:
Improper subset: {}, {1}, {3}, {5}, {1,3}, {1,5}, {3,5} and {1,3,5}
Improper Subset Formula
For a collection of ‘n’ elements, the number of improper subsets is always 1. In other words, the number of improper subsets of a set is independent of the number of its elements.
Learn More, Set Theory Formulas
Proper and Improper Subsets
The key differences between proper subsets and improper subsets are listed in the following table:
|
Proper Subset
|
Improper Subset
|
|
It contains some of the elements of a set.
|
It contains all the elements of a set.
|
|
It will never equal to a give set.
|
It is always equal to a given set.
|
|
The number of proper subsets of a set with ‘n’ elements is 2n – 1.
|
For a collection of ‘n’ elements, the number of improper subsets is always 1.
|
|
“⊂” symbol is used only for proper subsets.
|
“⊆” symbol is used for improper subsets.
|
Example: For a set P = {1,2} find proper and improper subset.
Solution:
Proper set is given by { }, {1} and {2}
Improper set is given by { }, {1}, {2} and {1,2}
Subsets vs Supersets
The key differences between both subsets and supersets are listed in the following table:
| Aspect |
Subset |
Superset |
| Definition |
A subset is a set that contains fewer or the same elements as another set. |
A superset is a set that contains all or more elements than another set. |
| Relationship |
The subset relationship is denoted as A ⊆ B, where A is a subset of B. |
The superset relationship is denoted as A ⊇ B, where A is a superset of B. |
| Example |
{1, 2} is a subset of {1, 2, 3}. |
{1, 2, 3} is a superset of {1, 2}. |
| Size |
The subset’s size is less than or equal to the superset’s size. |
The superset’s size is greater than or equal to the subset’s size. |
| Inclusion |
All elements of a subset are also elements of the superset. |
A superset includes all elements of the subset and possibly more. |
| Relationships |
A set can have multiple subsets. |
A set can have multiple supersets. |
| Empty Set |
The empty set (∅) is a subset of every set. |
The empty set (∅) is a superset of every set. |
Subset Fomula
All the formulas related to subsets are give below.
- The number of subsets of a set with n elements is 2n. This includes both proper and improper subsets.
- The number of proper subsets of a set with n elements is 2n – 1.
- The number of improper subsets of any set is always 1.
Also, Read
Solved Problems on Subsets
Problem 1: How many subsets in a set with 4 elements?
Solution:
A set containing 4 elements will have 24 elements in it = 16.
Problem 2: How many subsets in a set with 5 elements?
Solution:
A set containing 5 elements will have 25 elements in it = 32.
FAQs on Subsets
What are Subsets in Maths?
If every component of Set A is also present in Set B, then Set A is said to be a subset of Set B. To put it another way, Set B contains Set A.
What are Proper Subsets?
A subset of a set A that is not equal to A is a proper subset of A. In other words, if B is a proper subset of A, then A has at least one element that is not in B but all of B’s elements are in A.
What are Improper Subsets?
A subset that includes every component of the original set is considered an inappropriate subset.
Can a Subset be Equal to Itself?
Every set is thought of as a subset of itself. The proper subset of no set is itself. Every set has the empty set as a subset.
Can a Subset be a Universal Set?
We can say that set A is the subset of set B if every element in set A is also an element in set B. Then, any given universal set can be used to produce the subsets. It’s also important to keep in mind that every universal set is actually a subset of itself.
Can a Subset be Null?
Yes, a null set is by default subset of any set.
What are the two classifications of subset?
The classifications of subsets are:
- Proper subset
- Improper subset
Share your thoughts in the comments
Please Login to comment...