Split array into minimum number of subarrays having GCD of its first and last element exceeding 1
Last Updated :
10 Aug, 2021
Given an array arr[] of size N, the task is to split the entire array into a minimum number of subarrays such that for each subarray, the GCD of the first and last element of the subarray is greater than 1.
Examples:
Input: arr[] = {2, 3, 4, 4, 4, 3}
Output: 2
Explanation:
Split the given array into [2, 3, 4, 4, 4] and [3].
The first subarray has gcd(2, 4) = 2 which is more than 1 and
The second subarray has gcd(3, 3) = 3 which is also more than 1.
Input: arr[] = {1, 2, 3}
Output: 0
Explanation:
There is no possible splitting of the given array into subarrays in which the GCD of first and last element of the subarray is more than 1.
Naive Approach: The simplest approach to solve the problem is to perform all possible splits in the given array and for each split, check if all the subarrays have GCD of its first and last element greater than 1 or not. For all subarrays for which it is found to be true, store the count of subarrays. Finally, print the minimum count obtained among those splits.
Time Complexity: O(2N)
Auxiliary Space: O(1)
Efficient Approach: The approach is based on the idea that the first and the last element of the original array will always be used. The first element will be used in the first subarray split, the last element will be used in the last subarray split. To minimize the count of valid subarrays, follow the steps below:
- Fix a right pointer to the last element of the original array arr[], and find the leftmost element in the original array such that GCD(left, right) > 1. If such an element is not found, there is no valid answer.
- If such an element is found, that means we have found a valid subarray. Then change the right pointer to (left – 1), and again start searching for a valid subarray.
- Repeat the above step until right is more than 0 and keep on increasing the count of subarrays found till now.
- Print the value of count after all the above steps.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minSubarrays(int arr[], int n)
{
int right = n - 1;
int left = 0;
int subarrays = 0;
while (right >= 0) {
for (left = 0; left <= right;
left += 1) {
if (__gcd(arr[left],
arr[right])
> 1) {
subarrays += 1;
right = left - 1;
break;
}
if (left == right
&& __gcd(arr[left],
arr[right])
== 1) {
return 0;
}
}
}
return subarrays;
}
int main()
{
int N = 6;
int arr[] = { 2, 3, 4, 4, 4, 3 };
cout << minSubarrays(arr, N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int minSubarrays(int arr[], int n)
{
int right = n - 1;
int left = 0;
int subarrays = 0;
while (right >= 0)
{
for (left = 0; left <= right; left += 1)
{
if (__gcd(arr[left],
arr[right]) > 1)
{
subarrays += 1;
right = left - 1;
break;
}
if (left == right &&
__gcd(arr[left],
arr[right]) == 1)
{
return 0;
}
}
}
return subarrays;
}
static int __gcd(int a, int b)
{
return b == 0 ? a : __gcd(b, a % b);
}
public static void main(String[] args)
{
int N = 6;
int arr[] = {2, 3, 4, 4, 4, 3};
System.out.print(minSubarrays(arr, N));
}
}
|
Python3
from math import gcd
def minSubarrays(arr, n):
right = n - 1
left = 0
subarrays = 0
while (right >= 0):
for left in range(right + 1):
if (gcd(arr[left], arr[right]) > 1):
subarrays += 1
right = left - 1
break
if (left == right and
__gcd(arr[left],
arr[right]) == 1):
return 0
return subarrays
if __name__ == '__main__':
N = 6
arr = [ 2, 3, 4, 4, 4, 3 ]
print(minSubarrays(arr, N))
|
C#
using System;
class GFG{
static int minSubarrays(int[] arr, int n)
{
int right = n - 1;
int left = 0;
int subarrays = 0;
while (right >= 0)
{
for (left = 0; left <= right; left += 1)
{
if (__gcd(arr[left],
arr[right]) > 1)
{
subarrays += 1;
right = left - 1;
break;
}
if (left == right &&
__gcd(arr[left],
arr[right]) == 1)
{
return 0;
}
}
}
return subarrays;
}
static int __gcd(int a, int b)
{
return b == 0 ? a : __gcd(b, a % b);
}
public static void Main()
{
int N = 6;
int[] arr = {2, 3, 4, 4, 4, 3};
Console.Write(minSubarrays(arr, N));
}
}
|
Javascript
<script>
function minSubarrays(arr , n) {
var right = n - 1;
var left = 0;
var subarrays = 0;
while (right >= 0) {
for (left = 0; left <= right; left += 1) {
if (__gcd(arr[left], arr[right]) > 1) {
subarrays += 1;
right = left - 1;
break;
}
if (left == right && __gcd(arr[left], arr[right]) == 1) {
return 0;
}
}
}
return subarrays;
}
function __gcd(a , b) {
return b == 0 ? a : __gcd(b, a % b);
}
var N = 6;
var arr = [ 2, 3, 4, 4, 4, 3 ];
document.write(minSubarrays(arr, N));
</script>
|
Time Complexity: O(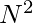 )
)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...