Shortest distance from the center of a circle to a chord

Given a circle which has a chord inside it. The length of the chord and the radius of the circle are given. The task is to find the shortest distance from the chord to the center.
Examples:

Input: r = 4, d = 3 
Output: 3.7081

Input: r = 9.8, d = 7.3
Output: 9.09492

Approach: 

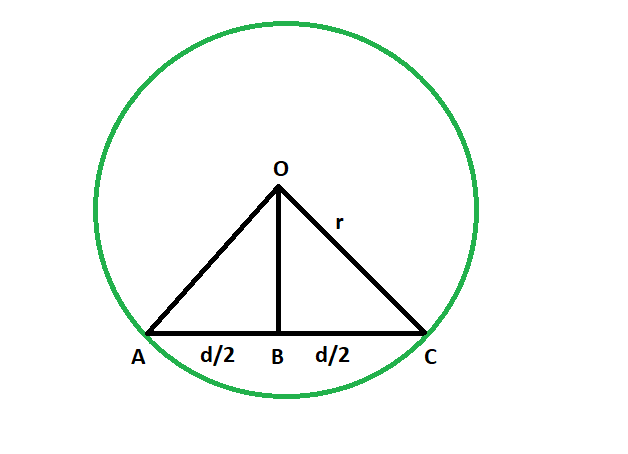
• We know that the line segment that is dropped from the center on the chord bisects the chord. The line is the perpendicular bisector of the chord, and we know the perpendicular distance is the shortest distance, so our task is to find the length of this perpendicular bisector.
• let radius of the circle = r
• length of the chord = d
• so, in triangle OBC,
  from Pythagoras theorem, 
  OB^2 + (d/2)^2 = r^2
  so, OB = √(r^2 – d^2/4)
• So, 

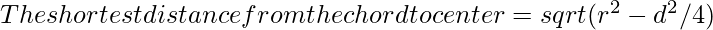
Below is the implementation of the above approach:  

C++

// C++ program to find
// the shortest distance from
// chord to the center of circle
#include <bits/stdc++.h>
using namespace std;

// Function to find the shortest distance
void shortdis(double r, double d)
{
    cout << "The shortest distance "
         << "from the chord to center "
         << sqrt((r * r) - ((d * d) / 4))
         << endl;
}

// Driver code
int main()
{
    double r = 4, d = 3;
    shortdis(r, d);
    return 0;
}

Java

// Java program to find
// the shortest distance from
// chord to the center of circle
class GFG
{

// Function to find the shortest distance
static void shortdis(double r, double d)
{
    System.out.println("The shortest distance "
        + "from the chord to center "
        + (Math.sqrt((r * r) - ((d * d) / 4))));
}

// Driver code
public static void main(String[] args)
{
    double r = 4, d = 3;
    shortdis(r, d);
}
}

/* This code contributed by PrinciRaj1992 */

Python3

# Python program to find
# the shortest distance from
# chord to the center of circle

# Function to find the shortest distance
def shortdis(r, d):
    print("The shortest distance ",end="");
    print("from the chord to center ",end="");
    print(((r * r) - ((d * d) / 4))**(1/2));

# Driver code
r = 4;
d = 3;
shortdis(r, d);

# This code has been contributed by 29AjayKumar

C#

// C# program to find
// the shortest distance from
// chord to the center of circle
using System;

class GFG
{

    // Function to find the shortest distance
    static void shortdis(double r, double d)
    {
        Console.WriteLine("The shortest distance "
            + "from the chord to center "
            + (Math.Sqrt((r * r) - ((d * d) / 4))));
    }

    // Driver code
    public static void Main()
    {
        double r = 4, d = 3;
        shortdis(r, d);
    }
}

// This code is contributed by AnkitRai01

PHP

<?php

// PHP program to find
// the shortest distance from
// chord to the center of circle


// Function to find the shortest distance
function shortdis($r,  $d)
{
    echo "The shortest distance ";
    echo "from the chord to center ";
    echo sqrt(($r * $r) - (($d * $d) / 4));
}

// Driver code
    $r = 4;
    $d = 3;
    shortdis($r, $d);

// This code is contributed by Naman_Garg.

?>

Javascript

<script>

// JavaScript program to find
// the shortest distance from
// chord to the center of circle

// Function to find the shortest distance
function shortdis(r, d)
{
    document.write("The shortest distance "
        + "from the chord to center "
        + Math.sqrt((r * r) - ((d * d) / 4))
        + "<br>");
}

// Driver code

    let r = 4, d = 3;
    shortdis(r, d);

// This code is contributed by Surbhi Tyagi.

</script>

Output:

The shortest distance from the chord to centre 3.7081

Time Complexity: O(1)

Auxiliary Space: O(1)