Scrum Testing
Last Updated :
16 Sep, 2021
Scrum testing is a type of software testing that is performed to check the ability of the software or application to execute complicated processes. This testing also checks various other parameters of the software like quality, usability and performance. Execution of complex process needs complex software. Hence in order to make a complex software, scrum testing is required.
Objectives of Scrum Testing:
The objective of Scrum Testing is:
- To check the complexity of the software.
- To test the quality of the software.
- To test the performance of the software.
- To test the usability of the software.
- To support in unit testing.
Characteristics of Scrum Testing:
Following are the characteristics of the scrum testing:
- Scrum testing has some sequences that are repeated continuously.
- Scrum testing has life cycles that expire after some time.
- Scrum testing has fixed schedule for each cycle.
- Basically depends on the some key gadgets of the development.
Key attributes of the Scrum Testing:
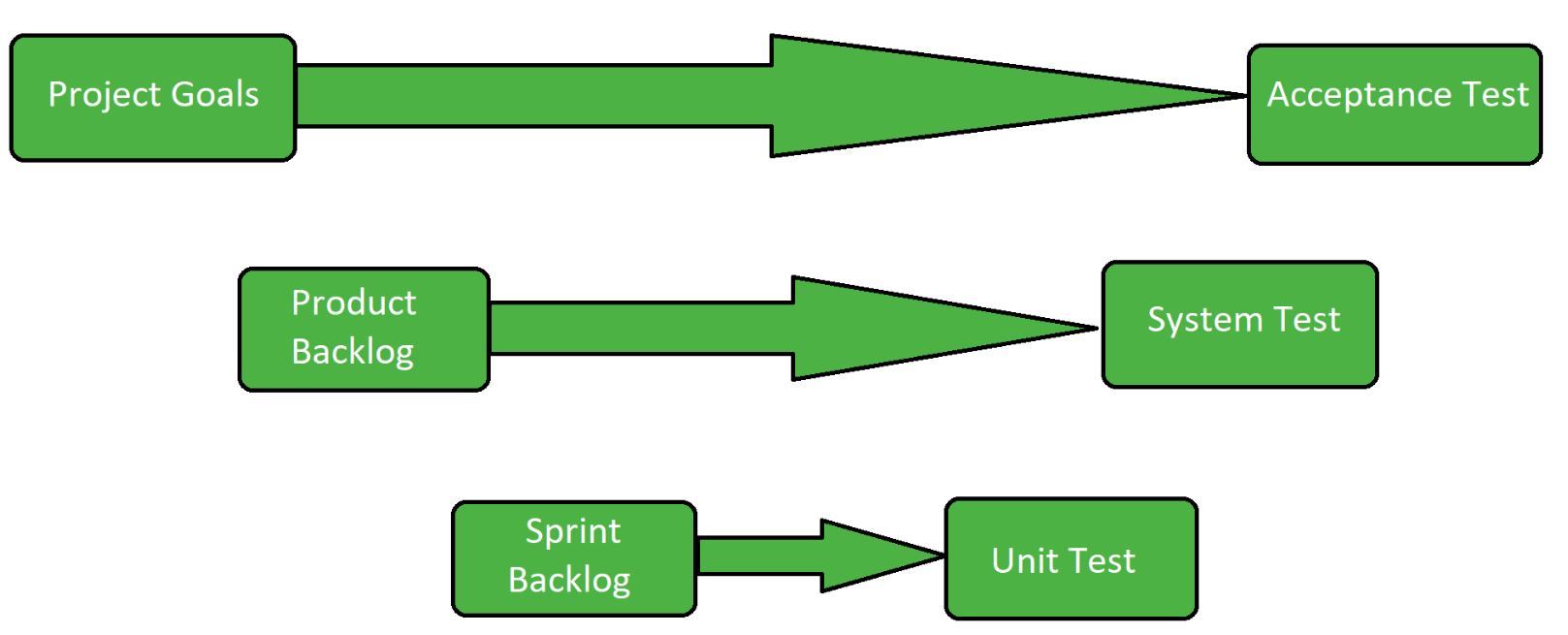
Project Goals:
It includes the basic idea behind the project and the requirement of the software. It basically focuses on whether the software satisfies the basic requirements or not. It involves all the planning and the requirement analysis phase. It consists several other attributes involved in it.
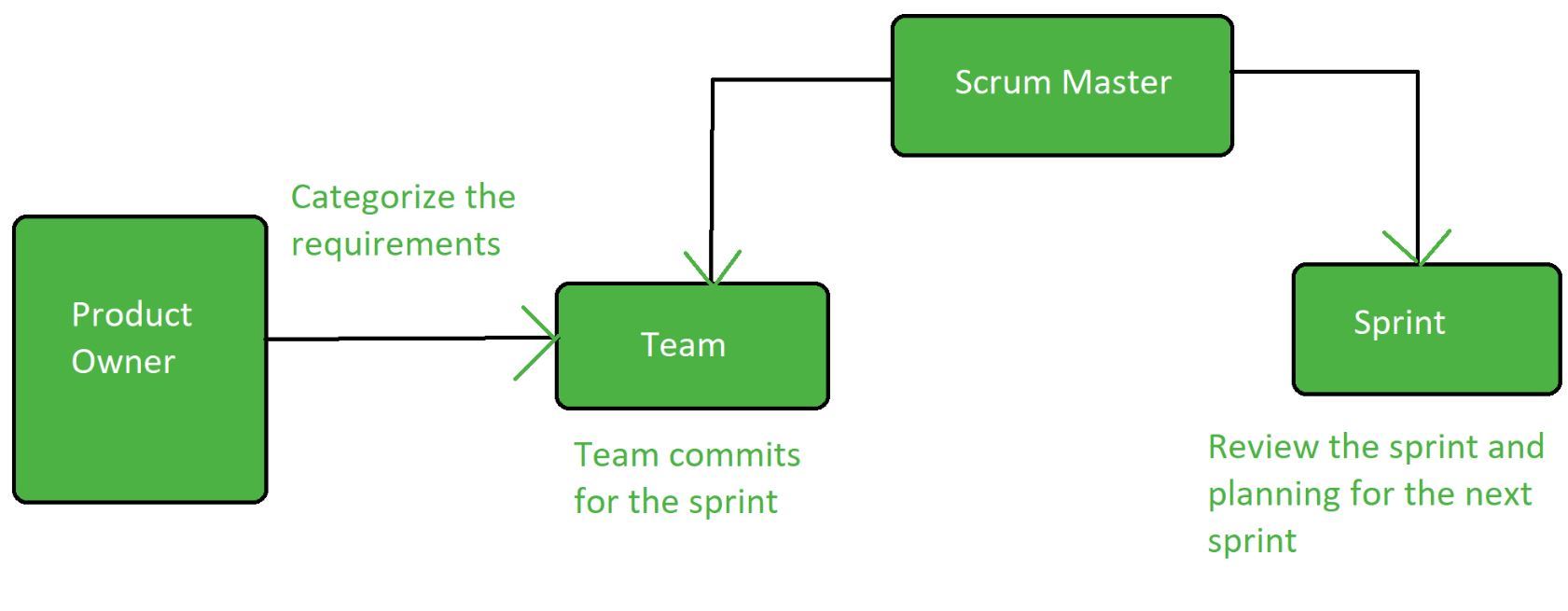
Product Backlog:
Product backlog is a collection of user experiences observed for a scrum product. The owner of the product prepares and maintains the product backlog. It is categorized by the product owner and anyone can add to it with consent from the product owner.
Sprint Backlog:
Sprint backlog is a collection of user experiences to be completed in a sprint. Work is not assigned during the sprint backlog and the team signs up for work on their own. It is owned and managed by the team. The remaining estimated work is updated daily. It is the collection of the tasks that are to be performed in Sprint.
Advantages of Scrum Testing:
The advantages of scrum testing are:
- It helps in determining the quality of the software.
- It helps in unit testing.
- It helps in building complicated software.
Share your thoughts in the comments
Please Login to comment...