Program to find number of solutions in Quadratic Equation

Last Updated : 22 Apr, 2021

Given an equation 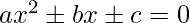$ax^{2}\pm bx\pm c=0$ with value a, b, and c, where a and b is any value and c is constant, find how many solutions thus this quadratic equation have?
Examples:

Input :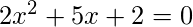 
Output : 2 solutions
Input : 
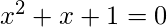Output : no solution

Solution:
To check whether the equation has a solution or not, quadratic formula for discriminant is used.

The formula is given as, 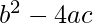$b^{2}-4ac$

Respective conditions are given as,

if the discriminant is positive 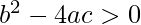$b^{2}-4ac> 0$ , then the quadratic equation has two solutions.
if the discriminant is equal 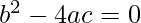$b^{2}-4ac= 0$ , then the quadratic equation has one solution.
if the discriminant is negative 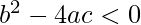$b^{2}-4ac< 0$ , then the quadratic equation has no solution.

Programs:

C++

// C++ Program to find the solutions of specified equations
#include <iostream>
using namespace std;
 
// Method to check for solutions of equations
void checkSolution(int a, int b, int c)
{
 
    // If the expression is greater than 0, then 2 solutions
    if (((b * b) - (4 * a * c)) > 0)
        cout << "2 solutions";
 
    // If the expression is equal 0, then 2 solutions
    else if (((b * b) - (4 * a * c)) == 0)
        cout << "1 solution";
 
    // Else no solutions
    else
        cout << "No solutions";
}
 
int main()
{
    int a = 2, b = 5, c = 2;
    checkSolution(a, b, c);
    return 0;
}

Java

// Java Program to find the solutions of specified equations
public class GFG {
 
    // Method to check for solutions of equations
    static void checkSolution(int a, int b, int c)
    {
 
        // If the expression is greater than 0,
        // then 2 solutions
        if (((b * b) - (4 * a * c)) > 0)
            System.out.println("2 solutions");
 
        // If the expression is equal 0, then 2 solutions
        else if (((b * b) - (4 * a * c)) == 0)
            System.out.println("1 solution");
 
        // Else no solutions
        else
            System.out.println("No solutions");
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int a = 2, b = 5, c = 2;
        checkSolution(a, b, c);
    }
}

Python3

# Python3 Program to find the
# solutions of specified equations
 
# function to check for
# solutions of equations
def checkSolution(a, b, c) :
 
    # If the expression is greater
    # than 0, then 2 solutions
    if ((b * b) - (4 * a * c)) > 0 :
        print("2 solutions")
 
    # If the expression is equal 0,
    # then 1 solutions
    elif ((b * b) - (4 * a * c)) == 0 :
        print("1 solution")
 
    # Else no solutions
    else :
        print("No solutions")
 
# Driver code
if __name__ == "__main__" :
 
    a, b, c = 2, 5, 2
    checkSolution(a, b, c)
 
# This code is contributed
# by ANKITRAI1

C#

// C# Program to find the solutions
// of specified equations
using System;
class GFG
{
 
// Method to check for solutions of equations
static void checkSolution(int a, int b, int c)
{
 
    // If the expression is greater
    // than 0, then 2 solutions
    if (((b * b) - (4 * a * c)) > 0)
        Console.WriteLine("2 solutions");
 
    // If the expression is equal to 0,
    // then 2 solutions
    else if (((b * b) - (4 * a * c)) == 0)
        Console.WriteLine("1 solution");
 
    // Else no solutions
    else
        Console.WriteLine("No solutions");
}
 
// Driver Code
public static void Main()
{
    int a = 2, b = 5, c = 2;
    checkSolution(a, b, c);
}
}
 
// This code is contributed by inder_verma

PHP

<?php
// Program to find the solutions
// of specified equations
 
// Method to check for solutions
// of equations
function checkSolution($a, $b, $c)
{
 
    // If the expression is greater
    // than 0, then 2 solutions
    if ((($b * $b) - (4 * $a * $c)) > 0)
        echo "2 solutions";
 
    // If the expression is equal 0,
    // then 2 solutions
    else if ((($b * $b) -
              (4 * $a * $c)) == 0)
        echo "1 solution";
 
    // Else no solutions
    else
        echo"No solutions";
}
 
// Driver Code
$a = 2; $b = 5; $c = 2;
checkSolution($a, $b, $c);
 
// This code is contributed
// by inder_verma
?>

Javascript

<script>
 
// Javascript Program to find the solutions
// of specified equations
 
// Method to check for solutions of equations
function checkSolution(a, b, c)
{
     
    // If the expression is greater than 0,
    // then 2 solutions
    if (((b * b) - (4 * a * c)) > 0)
        document.write("2 solutions");
 
    // If the expression is equal 0, then 2 solutions
    else if (((b * b) - (4 * a * c)) == 0)
        document.write("1 solution");
 
    // Else no solutions
    else
        document.write("No solutions");
}
 
// Driver Code
var a = 2, b = 5, c = 2;
 
checkSolution(a, b, c);
 
// This code is contributed by Ankita saini
 
</script>

Output:

2 solutions

Attention reader! All those who say programming isn’t for kids, just haven’t met the right mentors yet. Join the Demo Class for First Step to Coding Course, specifically designed for students of class 8 to 12.

The students will get to learn more about the world of programming in these free classes which will definitely help them in making a wise career choice in the future.

My Personal Notes

Related Articles

Program to find number of solutions in Quadratic Equation

C++

Java

Python3

C#

PHP

Javascript