Puzzle | Tricky Matchstick Problem (move 3 matchsticks to get 3 squares)
Last Updated :
18 Jan, 2023
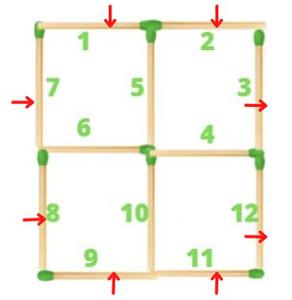
Puzzle: A matchstick puzzle is given below, move 3 matchsticks to get 3 squares. Give all the possibly unique solutions for the given problem.

Solution:
Let’s discuss a step-by-step solution to arrive at a result.
1. Count the total number of matchsticks available in the problem. In the figure, the total number of matchsticks is equal to 12 as shown below figure.

2. Now for making a square 4 sticks are used so, to form 4 squares 16 sticks would have been used but we have only 12 sticks. Here the concept of sticks common between two adjacent unit shapes comes.

Sticks 5,4,6,10 are common matchsticks
3. Now to make 3 squares 4 * 3 = 12 sticks are required (at max, when sticks are not common between squares). And in this case, 12 matchsticks are available. Now, all we have to do is-
- Eliminate all 4 common sticks.
- Form 3 independent squares,
- By moving just 3 sticks.
4. Concept of promising stick
- Interestingly, if any one of the 12 sticks is moved first, at least two common sticks will lose their common properties. In moving any of the four common sticks, immediately 4 free-standing sticks will occur. This is impossible to accomplish in the remaining two moves. Therefore, the first stick move eliminating two common sticks cannot be a common stick.
- Eight of the remaining sticks (1, 2, 3, 12, 11, 9, 8, 7) can be moved first, as all 8 sticks share the same position, function, and location within the structure. These are the corner sticks. These are the Promising sticks.
Marked sticks are promising sticks
Solution 1: Common stick elimination technique
Number 4 cannot be split into three positive integers with a minimum value of 1. One of the three numbers has to be 2. By applying Reasoning, 4 common sticks can be eliminated in just 3 moves as-
1. Move stick numbered 2 first. This destroys 1 square and eliminates 2 common match sticks.

2. Move stick numbered 3. This results in two free sticks gained, two common sticks eliminated (like 5, 4 are not common sticks now) and 1 square reduced.

3. Move 3rd stick such that it eliminates 2 more common sticks and destroys 1 more square.
Note:
Any of the four sticks numbered 1,7,11,12 belonging to the two squares adjacent to the square destroyed just now cannot be removed as it would eliminate 1 more common stick, destroy 1 more square, however would create two unplaced sticks and the situation could be not possible to manipulate.
The only feasible solution for this step is to select stick 8.

3 Squares are formed
Hence 3 more solutions can be concluded by this method as shown.
Solution 2: If sticks 1,7,12 are considered for movement instead of 2,3,8 in the first solution.

Solution 3: If sticks 1,7,11 are considered for movement instead of 2,3,8 in the first solution.

Solution 4: If sticks 8,9,2 are considered for movement instead of 2,3,8 in the first solution.

Share your thoughts in the comments
Please Login to comment...