Puzzle 80 | Tic Tac Toe revisited
Last Updated :
18 Jan, 2023
Ank and Mini play a game of tick-tack-toe. In this game, the players try to get three circles or three crosses in a row (horizontal, vertical, or diagonal).
They follow the following rules:
- A player always tries to win: if a player can place his own symbol (X or O) in a row that already contains two of his own symbols, he will do so.
- A player always tries to avoid that his opponent wins: if a player can place his own symbol (X or O) in a row that already contains two of the symbols of his opponent, he will do so.
Of course, the first rule has precedence over the second rule, because the game can be won in this way.
In the game shown on the right, six moves have been made. Ank plays with crosses (X) and Mini plays with circles (0). However, we do not know who started the game. Who will win the game?
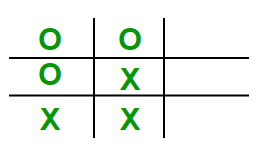
Solution:
It is clear that if we know who made the sixth move, we also know who can make the seventh move and wins. If Mini (circles) has made the sixth move, there are three possibilities for the situation after five moves:

Based on the rules of the game, only possibility 1 could have resulted in the situation after six moves. In that case, there are three possibilities for the situation after four moves:

Based on the rules of the game, Ank (crosses) would have made the winning move, which however did not happen. From this, we can conclude that Ank did not make the fifth move and Mini did not make the sixth move. Therefore, Ank must have made the sixth move and Mini can make the seventh, winning move!
To check that Ank could indeed have made the sixth move, we look at the following three possibilities after five moves:
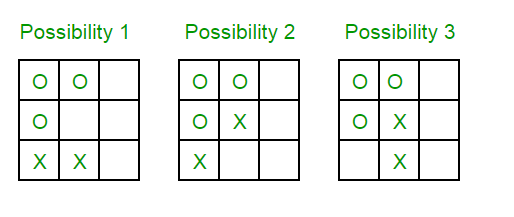
Based on the rules of the game, only possibility 3 can result in the situation after six moves. Therefore, Ank could indeed have made the sixth move.
Conclusion: Ank has made the sixth move, and Mini will make the seventh move and win.
You may also like – Tic Tac Toe
This puzzle is contributed by Praveer Satyam.
Share your thoughts in the comments
Please Login to comment...