Properties of z-Transforms
Last Updated :
17 Apr, 2024
Prerequisite: What is Z-transform?
A z-Transform is important for analyzing discrete signals and systems. In this article, we will see the properties of z-Transforms. These properties are helpful in computing transforms of complex time-domain discrete signals.
1. Linearity: If we have two sequences x1[n] and x2[n], and their individual z-transforms as X1(z) and X2(z), then the linearity property permits us to write:
![Rendered by QuickLaTeX.com \begin{aligned}X(z) & = Z { ax_{1}[n]+bx_{2}[n] } \\ & = aX_{1}(z) + bX_{2}(z)\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8f91f7d2f2d18768e5e18ccd7a7ec3f3_l3.png)
This is easily proved. First consider ![Rendered by QuickLaTeX.com x[n]=ax_{1}[n]+bx_{2}[n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8acd094544a67c93dc1226f490e4edb6_l3.png)
Then, from the definition, we see:
![Rendered by QuickLaTeX.com \begin{aligned}X(z)&= \sum _{ n=0 }^{ \infty }{ } x[n]z^{-n}\\&= \sum _{ n=0 }^{ \infty }{ }( ax_{1}[n]+bx_{2}[n])z^{-n}\\&= a\sum _{ n=0 }^{ \infty }x_{1}[n]z^{-n}+b\sum _{ n=0 }^{ \infty }x_{2}[n]z^{-n} \\&= aX_{1}(z) + bX_{2}(z)\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3be49d67051c7f260b143f68adf1f464_l3.png)
2. Time Shifting: If we have a time-shifted sequence such as x[n-k], then its z-transform is given by Z{ x[n-k]} = z^{-k}X(z).
Let’s take n – k = m, i.e., n = k + m and y[n] = x[n-k]. Now here we are assuming that x[n] starts from n=0, hence x[n-k] starts from n=k, or n-k=0, or from m=0.
![Rendered by QuickLaTeX.com \begin{aligned}Y(z) & = \sum_{m=0}^{\infty }y[n]z^{-n} \\& = \sum_{m=0}^{\infty }x[n-k]z^{-n} \\&= \sum_{m=0}^{\infty }x[m]z^{-m-k} \\& = z^{-k}\sum_{m=0}^{\infty }x[m]z^{-m} \\&= z^{-k}X(z)\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cda9acb1d0b54c1cd68d61bb0127bc1f_l3.png)
3. Time reversal: Time reversal property states that ![Rendered by QuickLaTeX.com Z{ x[-n]} = X(1/z)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14e7aef1c24885ce567638ba50d1e0d8_l3.png)
We are going to formally prove this statement by taking y[n]=x[-n].
![Rendered by QuickLaTeX.com \begin{aligned} \sum_{n=0}^{\infty }y[n]z^{-n} = \sum_{n=0}^{\infty }x[-n]z^{-n}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68f3a0937ee9ce4f7f3616595bee508e_l3.png)
Now let’s take -n=m. Then
![Rendered by QuickLaTeX.com \begin{aligned}\sum_{m=0}^{ -\infty}x[m]z^{m} & = \sum_{m=-\infty}^{0 }x[m]z^{m}\\ & = \sum_{-m=\infty}^{0 }x[m](z^{-1})^{-m}\\ & = X(z^{-1})\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac4d3aa05b2dacf418418157fec39110_l3.png)
4. Scaling in z domain: When we multiply the signal sequence x[n] in the time domain with an exponential factor an, the equivalent z-transform of the new signal is scaled by a factor of a.
Basically, ![Rendered by QuickLaTeX.com Z{ anx[n]}=X(z/a)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1a8b172495430b434d54d3ed65333801_l3.png) .
.
Proof is elementary and is shown below.
![Rendered by QuickLaTeX.com \begin{aligned} \sum _{ n=0 }^{ \infty } a^{n}x[n]z^{-n} & = \sum _{ n=0 }^{ \infty } x[n](a^{-1}z)^{-n}\\ &=\sum _{ n=0 }^{ \infty } x[n](z/a)^{-n} \\ = X(z/a)\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a786042c220185584387aab2fe4dda98_l3.png)
5. Differentiation in z domain: We know: ![Rendered by QuickLaTeX.com X(z)=\sum_{n=0}^{\infty }x[n]z^{-n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f31a717429efa86a72d935c2e9400392_l3.png)
Differentiating with respect to z, we get
![Rendered by QuickLaTeX.com \begin{aligned} \frac{\mathrm{d} X(z)}{\mathrm{d} z} = -\sum_{n=0}^{\infty }nx[n]z^{-n-1} & \\ = -z^{-1} \sum_{n=0}^{\infty }nx[n]z^{-n}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6e3768ac90189541ece2364c996085f_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} -z\frac{\mathrm{d} X(z)}{\mathrm{d} z} & = \\ \sum_{n=0}^{\infty }(nx[n])z^{-n}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-412d0fc60b736d9da85553ea42edb678_l3.png)
Hence, we can deduce that for k differentiations, we get ![Rendered by QuickLaTeX.com Z{ n^kx[n]} = (-1)^kz^k\frac{\mathrm{d^{k}}X(z) }{\mathrm{d} z^{k}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74413b2b642883bc57fd1e6bcd89895e_l3.png)
6. Convolution: Convolution of two sequences x[n] and h[n] is defined as ![Rendered by QuickLaTeX.com x[n]*h[n]=\sum_{k=0}^{\infty }x[k]h[n-k]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-62ef7a3b67c40e5bd2d04b201fd4e20a_l3.png)
Now z-transforms of x[n] and h[n] are X(z) and H(z) respectively. Using this notation, we have
![Rendered by QuickLaTeX.com \begin{aligned}\sum_{n=0}^{\infty }(x[n]*h[n])z^{-n} =\sum_{n=0}^{\infty }\sum_{k=0}^{\infty }x[k]h[n-k]z^{-n}\\=\sum_{n=0}^{\infty }\sum_{k=0}^{\infty }x[k]h[n-k]z^{-(n-k)}z^{-k}\\ =\sum_{n=0}^{\infty }(\sum_{k=0}^{\infty }x[k]z^{-k})h[n-k]z^{-(n-k)}\\ =\sum_{n=0}^{\infty }X(z)h[n-k]z^{-(n-k)}\\ =X(z)\sum_{n-k=0}^{\infty }h[n-k]z^{-(n-k)}\\ =X(z)H(z)\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b801497009d0a25a628531abc90ea29_l3.png)
Hence, convolution in time domain is multiplication in z domain.
7. Initial value theorem: Initial value theorem gives us a tool to compute the initial value of the sequence x[n], that is, x[0] in the z domain by taking a limit of the value of X(z). It states that the following equivalence is feasible.
![Rendered by QuickLaTeX.com x[0] = \lim _{ z\rightarrow \infty } x(Z)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b652e3d0191cb7aaf00fbfc64458320b_l3.png)
The proof, as before, relies on the definition of X(z).
![Rendered by QuickLaTeX.com \begin{aligned} X(z) = \sum_{n=0}^{\infty }x[n]z^{-n} & \\ = x[0]z^0+x[1]z^{-1}+z[2]z^{-2}+....&\\ \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3accf33a458c787aaf883465eed00c4_l3.png)
Clearly, if we want to get x[0], we can make z approach to infinity so that all the other terms die out. What is left behind is precisely the statement of the theorem presented before.
8. Final value theorem: The final value theorem lets us know the final value of x[n], or the value at infinity of x[n], using appropriate limits of X(z).
It states that 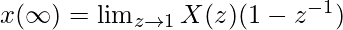
If we take the z transform of x[n]-x[n-1], then we get ![Rendered by QuickLaTeX.com \begin{aligned} X(z)-z^{-1}X(z) & =\sum_{n=0}^{\infty }x[n]z^{-n}-z^{-1} \sum_{n=0}^{\infty }x[n]z^{-n} \\& = x[0]+x[1]z^{-1}+x[2]z^{-2}+...-z^{-1}(x[0]+x[1]z^{-1}+x[2]z^{-2}+...) \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddf508186f3ae937a6ac23cee6c0b6fa_l3.png)
Now taking the limit z⇢1, we see that we get ![Rendered by QuickLaTeX.com x[1]-x[0]+x[2]-x[1]+x[3]-x[2]+...+x[\infty]-x[\infty -1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-29cef92b55a0f28b1b75413ab7e74c0e_l3.png) in the right hand side, which simplifies to x[\infty] basically. Hence the theorem is proved.
in the right hand side, which simplifies to x[\infty] basically. Hence the theorem is proved.
9. Multiplication in time property
x1[n].x2[n]=1/j2pi {X1[z]*X2[z]}
10. Accumulation property
Share your thoughts in the comments
Please Login to comment...