4-bit binary Adder-Subtractor
Last Updated :
16 Dec, 2022
In Digital Circuits, A Binary Adder-Subtractor is capable of both the addition and subtraction of binary numbers in one circuit itself. The operation is performed depending on the binary value the control signal holds. It is one of the components of the ALU (Arithmetic Logic Unit).
This Circuit Requires prerequisite knowledge of Exor Gate, Binary Addition and Subtraction, and Full Adder.
Let’s consider two 4-bit binary numbers A and B as inputs to the Digital Circuit for the operation with digits
A0 A1 A2 A3 for A
B0 B1 B2 B3 for B
The circuit consists of 4 full adders since we are performing operations on 4-bit numbers. There is a control line K that holds a binary value of either 0 or 1 which determines that the operation is carried out is addition or subtraction.
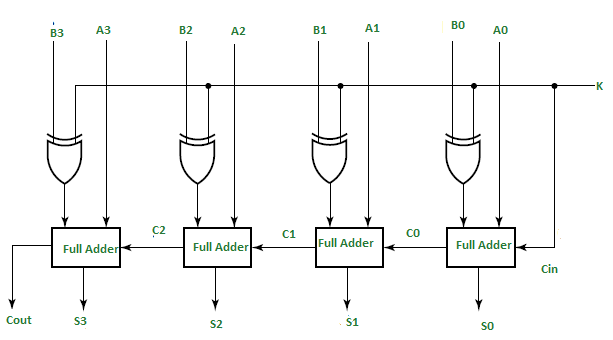
As shown in the figure, the first full adder has a control line directly as its input(input carry Cin), The input A0 (The least significant bit of A) is directly input in the full adder. The third input is the exor of B0 and K. The two outputs produced are Sum/Difference (S0) and Carry (C0).
If the value of K (Control line) is 1, the output of B0(exor)K=B0′(Complement B0). Thus the operation would be A+(B0′). Now 2’s complement subtraction for two numbers A and B is given by A+B’+Cin. This suggests that when K=1, the operation being performed on the four-bit numbers is subtraction.
Similarly If the Value of K=0, B0 (exor) K=B0. The operation is A+B which is simple binary addition. This suggests that When K=0, the operation is performed on the four-bit numbers in addition.
Then C0 is serially passed to the second full adder as one of it’s outputs. The sum/difference S0 is recorded as the least significant bit of the sum/difference. A1, A2, A3 are direct inputs to the second, third and fourth full adders. Then the third input is the B1, B2, B3 EXORed with K to the second, third and fourth full adder respectively. The carry C1, C2 are serially passed to the successive full adder as one of the inputs. C3 becomes the total carry to the sum/difference. S1, S2, S3 are recorded to form the result with S0.
For an n-bit binary adder-subtractor, we use n number of full adders.
Example:
Assume that we have two 3-bit numbers, i.e., X=100 and Y=011, and feed them in Full-Adder as an input.
X0 = 0 X1 = 0 X2 = 1
Y0 = 1 Y1 = 1 & Y2 = 0
For K=0:
Y0⨁K=Y0 and Cin=K=0
So, from first Full-Adder
S0 = X0+Y0+Cin
S0= 0+1+0
S0=1
C0=0
Similarly,
S1 = X1+Y1+C0
S1 = 0+1+0
S1=1 and C1=0
Similarly,
S2 = X2+Y2+C1
S2 = 1+0+0
S2=1 and C2=0
Thus,
X= 100 =4
Y = 011 = 3
Sum = 0111 = 7
For K=1
Y0⨁K=Y0' and Cin=k=1
So,
S0 = X0+Y0'+Cin
S0 = 0+0+1
S0=1 and C0=0
Similarly,
S1 = X1+Y1'+C0
S1 = 0+0+0
S1=0 and C1=0
Similarly,
S2 = X2+Y2'+C1
S2 = 1+1+0
S2=0 and C2=0
Thus,
X = 010 = 4
Y = 011 = 3
Difference = 001 = 1
Share your thoughts in the comments
Please Login to comment...