Properties of Minimum Spanning Tree (MST)
Last Updated :
26 Feb, 2023
For a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have multiple spanning trees.
A Spanning Tree is a tree which have V vertices and V-1 edges. All nodes in a spanning tree are reachable from each other.
A Minimum Spanning Tree(MST) or minimum weight spanning tree for a weighted, connected, undirected graph is a spanning tree having a weight less than or equal to the weight of every other possible spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree. In short out of all spanning trees of a given graph, the spanning tree having minimum weight is MST.
Necessary conditions for Minimum Spanning Tree:
- It must not form a cycle i.e, no edge is traversed twice.
- There must be no other spanning tree with lesser weight.
In this article, we will discuss the properties of MST:
Possible Multiplicity:
If G(V, E) is a graph then every spanning tree of graph G consists of (V – 1) edges, where V is the number of vertices in the graph and E is the number of edges in the graph. So, (E – V + 1) edges are not a part of the spanning tree. There may be several minimum spanning trees of the same weight. If all the edge weights of a graph are the same, then every spanning tree of that graph is minimum.
Consider a complete graph of three vertices and all the edge weights are the same then there will be three spanning trees(which are also minimal) of the same path length are possible. Below is the image to illustrate the same:
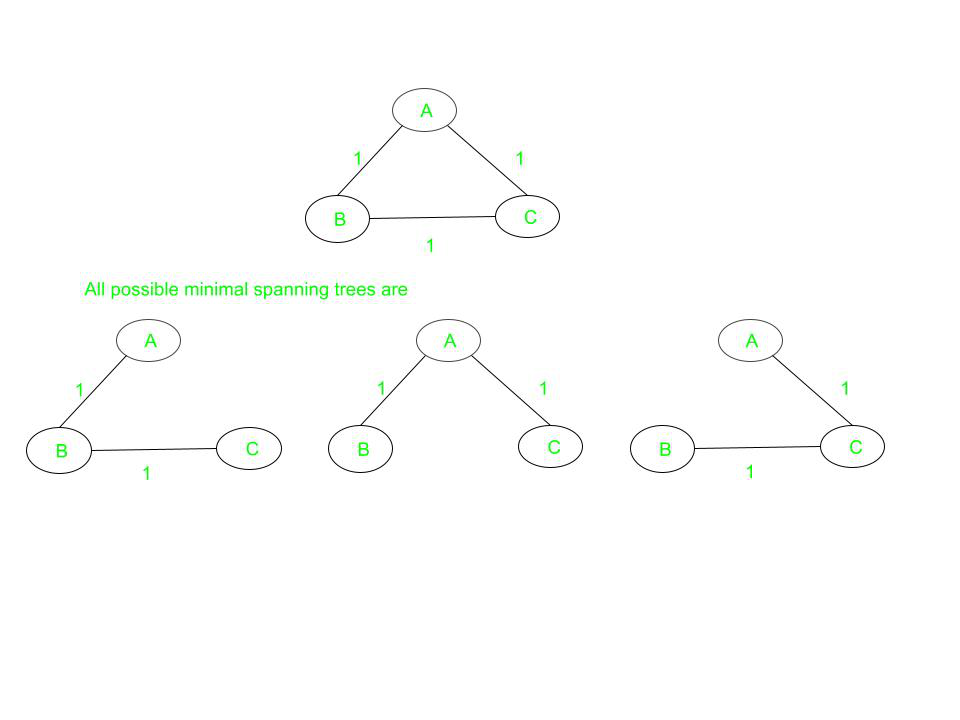
Each of the spanning trees has the same weight equal to 2.
Cut property:
For any cut C of the graph, if the weight of an edge E in the cut-set of C is strictly smaller than the weights of all other edges of the cut-set of C, then this edge belongs to all the MSTs of the graph. Below is the image to illustrate the same:

Cycle property:
For any cycle C in the graph, if the weight of an edge E of C is larger than the individual weights of all other edges of C, then this edge cannot belong to an MST. In the above figure, in cycle ABD, edge BD can not be present in any minimal spanning tree because it has the largest weight among all the edges in the cycle.
Uniqueness:
If each edge has a distinct weight then there will be only one, i.e., a unique minimum spanning tree.

Minimum Cost Subgraph
For all the possible spanning trees, the minimum spanning tree must have the minimum weight possible. However, there may exist some more spanning with the same weight that of minimum spanning tree, and those all may also be considered as Minimum Spanning tree.
- Minimum Cost Edge: If the minimum cost edge of a graph is unique, then this edge is included in any MST. For example, in the above figure, the edge AB (of the least weight) is always included in MST.
- If a new edge is added to the spanning tree then it will become cyclic because every spanning tree is minimally acyclic. In the above figure, if edge AD or BC is added to the resultant MST, then it will form a cycle.
- The spanning tree is minimally connected, i.e., if any edge is removed from the spanning tree it will disconnect the graph. In the above figure, if any edge is removed from the resultant MST, then it will disconnect the graph.
Algorithms for finding Minimum Spanning Tree(MST):-
- Prim’s Algorithm
- Kruskal’s Algorithm
Share your thoughts in the comments
Please Login to comment...