Laplace Transform in Circuit Analysis

The analysis of circuit analysis is a fundamental discipline in electrical engineering. It enables engineers to design and construct electrical circuits for several purposes. The Laplace transform is one of the powerful mathematical tools that play a vital role in circuit analysis. The Laplace transform, developed by Pierre-Simon Laplace in the late 18th century, is a mathematical technique that simplifies the analysis of complex linear time-invariant systems.

Laplace Transform

The Laplace transform is a mathematical operation or tool that converts a time domain function into the frequency domain. The frequency domain is represented by ‘s’ or ‘jω’.

It is used in the conversion of differential equations into algebraic equations, hence providing a powerful technique for analyzing linear time-invariant systems such as electrical circuits.

Mathematical Representation of Laplace Transform:

where x(t) is a time-domain function and is converted to frequency domain (X(s)).

Circuit Analysis using Laplace Transform

Laplace Transform is a strong mathematical tool to solve the complex circuit problems. It converts the time domain circuit to the frequency domain for easy analysis. To solve the circuit using Laplace Transform, we follow the following steps:

1. Write the differential equation of the given circuit.
2. Take the Laplace transform of the equation written.
3. Analysis of the s-domain equations.

An electrical circuit may have three important components, i.e., Resistor (R), Conductor (L), Capacitor (C). We will see the analysis of the circuit having these components using Laplace Transform.

1. Pure Resistive Circuit

The below given image represents a pure resistive circuit.

Figure 1: Pure Resistive Circuit

Applying KVL in figure 1(a):

v(t) = i(t)R —— (1)

Taking the Laplace transform of equation 1:

V(s) = I(s)R —— (2)

The equation 2 represents the Laplace Transform of equation 1.

Hence, the above analysis shows that the the resistance R is same time and frequency domain. Also, figure 1(b) shows the Laplace Transformed Circuit.

2. Pure Inductive Circuit

The below given image represents a pure inductive circuit.

Figure 2: Pure Inductive Circuit

Applying KVL in figure 2(a):

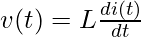—— (1)

Taking the Laplace transform of equation 1:

—— (2)

Here, 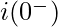is the initial current flowing through the conductor. The equation 2 represents the Laplace Transform of equation 1.

If the initial current flowing through the conductor is 0 then equation 2 will be:

V(s) = 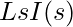—— (2)

Hence, the above analysis shows that the the inductor L in time-domain is converted to ‘sL’ in the frequency domain. Also, figure 2(b) shows the Laplace Transformed Circuit.

3. Pure Capacitive Circuit

The below given image represents a pure capacitive circuit.

Figure 3: Pure Capacitive circuit

Applying KVL in figure 3(a):

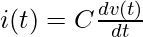—— (1)

Taking the Laplace transform of equation 1:

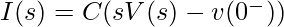
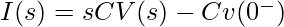
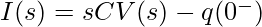
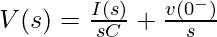——— (2)

Here, 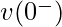is the initial voltage across the capacitor. The equation 2 represents the Laplace Transform of equation 1.

If the voltage across the capacitor is 0, i.e., capacitor is discharge then equation 2 will be:

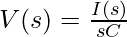
Hence, the above analysis shows that the capacitor C in time-domain is converted to ‘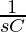‘ in the frequency domain. Also, figure 3(b) shows the Laplace Transformed Circuit.

Important Note for Laplace Transform in Circuit Analysis

Reactive Element Name	Reactive Element Symbol	Laplace Transform (if initial conditions are 0)
Resistor	R	R
Capacitor	C
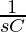
Inductor	L	sL

Why we Use the Laplace Transform in Circuit Analysis?

• Simplifies Differential Equations: It is very hard to solve complex differential equations which are used to explain many electrical circuits. These differential equations are transformed into algebraic equations using the Laplace transform, which are frequently simpler to work with and solve.

• Frequency Domain Analysis: To analyze the circuit in frequency domain, which is particularly helpful for figuring out how circuits react to various frequency components of input signals. It is useful in the fields like signal processing and filter design.

• Analysis of Time and Frequency: With the help of Laplace Transform we can easily switch from time to frequency domain and vice versa (using inverse Laplace Transform). It helps in efficient circuit analysis.

Solved Example: Laplace Transform in Circuit Analysis

Question: The given figure represents the RLC circuit. Find the output voltage of the given circuit in s-domain.

RLC Circuit

Solution:

Converting the circuit in the Laplace domain. It will help us to treat the capacitor and inductor as resistor.

The Laplace transformed circuit is given below:

Laplace Transformed circuit

Applying KVL in the above circuit:

Assuming the initial conditions are 0.

The output voltage is:

Advantages of Laplace Transform in Circuit Analysis

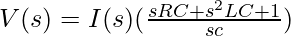
• Convolution Theorem: Laplace Transforms make it possible to implement the Convolution Theorem, which makes it simple to examine how linear time-invariant circuits respond to various input signals.

• Transient and Steady State Analysis: It is used to distinguish between transient and steady-state responses in transient and steady-state analysis. This separation simplifies the analysis of circuit behavior.

• Initial Conditions Handling: Laplace Transforms offer an intuitive method for handling initial conditions in circuit analysis. It is simpler to explain the state of the circuit at time t=0 since they become constants in the s-domain.

• Impulse Response Analysis: The s-domain model makes it simple to analyse a system’s impulse response, which is essential for knowing how a circuit reacts to abrupt changes or input spikes.

• Stability Analysis: Laplace transforms is used to analyze the stability of feedback control systems, which is essential for assuring the systems’ desired performance.

Disadvantages of Laplace Transform in Circuit Analysis

• Limited Applicability to Nonlinear Systems: It is best suited for linear systems, with limited applicability to nonlinear systems. They perform less well when analyzing circuits that contain nonlinear components like transistors and diodes, which might result in inaccurate analysis.

• Complexity of the Inverse Laplace Transform: Although Laplace Transforms make analysis simpler, returning from the s-domain to the time domain (inverse Laplace Transform) can be difficult and need typical mathematical methods.

• Hard to Determine Initial Conditions: It may be difficult to determine the initial conditions for a circuit at time t=0 in cases, particularly if the circuit has been functioning for a long period or if the original conditions are not clearly stated.

Applications of Laplace Transform in Circuit Analysis

• Control Systems: The Laplace transform is essential for control system analysis and design. It is used by engineers to evaluate the stability and effectiveness of control systems and to create controllers that meet the certain requirements.

• Signal processing: The Laplace transform helps with the analysis and manipulation of data in the frequency domain in applications like image processing and audio signal processing. It is helpful id noise reduction and signal enhancement.

• Filter Design: It is used to create filters which includes audio processing and communication. The bandwidth and cutoff frequency of filters may be precisely controlled using the Laplace transform.

FAQs on Laplace Transform in Circuit Analysis

1. Why do Laplace Transforms employ complex numbers (s-domain) rather than real numbers (time domain)?

Complex numbers make it possible to express both amplitude and phase data, which simplifies the analysis and helps us to deal with circuits having reactive elements.

2. Can Laplace Transforms be applied to non-linear circuits?

The main use of Laplace Transforms is in linear time-invariant circuits. When used to non-linear circuits, they may produce inaccurate results or necessitate further approximations.

3. How to choose the correct initial conditions while using Laplace Transforms?

The initial conditions must represent the state of the circuit at t=0. It is based on the circuit’s physical properties and the problem statement.