Program to Find the value of cos(nΘ)
Last Updated :
31 Aug, 2022
Given a value of cos(?) and a variable 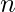 . The task is to find the value of cos(n?) using property of trigonometric functions.
. The task is to find the value of cos(n?) using property of trigonometric functions.
Note: n <= 15.
Examples:
Input : cos(?) = 0.5, n = 10
Output : -0.5
Input :cos(?) = 0.5, n = 3
Output : -0.995523
The problem can be solved using De moivre’s theorem and Binomial theorem as described below:
Using De-Moivre’s theorem, we have:
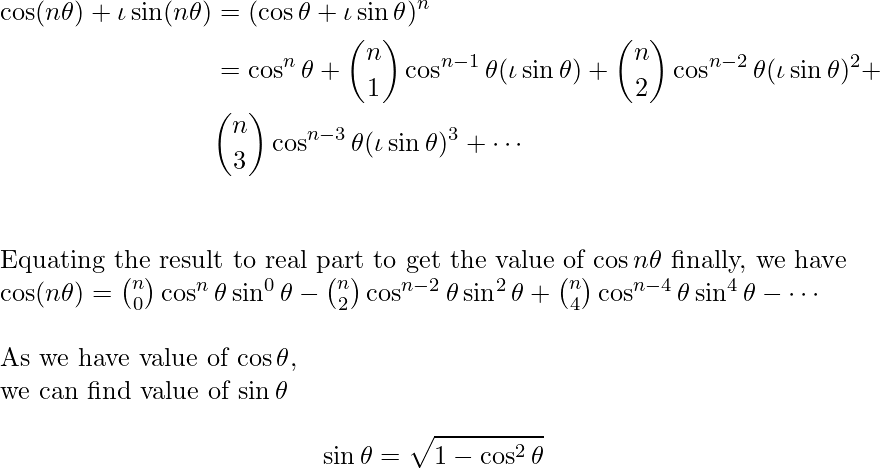
Now, as the value of both sin(?) and cos(?) is known. Put the values in above equation to get the answer.
Below is the implementation of the above idea:
C++
#include <bits/stdc++.h>
#define MAX 16
using namespace std;
int nCr[MAX][MAX] = { 0 };
void binomial()
{
for (int i = 0; i < MAX; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i)
nCr[i][j] = 1;
else
nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1];
}
}
}
double findCosnTheta(double cosTheta, int n)
{
double sinTheta = sqrt(1 - cosTheta * cosTheta);
double ans = 0;
int toggle = 1;
for (int i = 0; i <= n; i += 2) {
ans = ans + nCr[n][i] * pow(cosTheta, n - i) *
pow(sinTheta, i) * toggle;
toggle = toggle * -1;
}
return ans;
}
int main()
{
binomial();
double cosTheta = 0.5;
int n = 10;
cout << findCosnTheta(cosTheta, n) << endl;
return 0;
}
|
Java
class GFG
{
static int MAX=16;
static int[][] nCr=new int[MAX][MAX];
static void binomial()
{
for (int i = 0; i < MAX; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i)
nCr[i][j] = 1;
else
nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1];
}
}
}
static double findCosnTheta(double cosTheta, int n)
{
double sinTheta = Math.sqrt(1 - cosTheta * cosTheta);
double ans = 0;
int toggle = 1;
for (int i = 0; i <= n; i += 2) {
ans = ans + nCr[n][i] * Math.pow(cosTheta, n - i) *
Math.pow(sinTheta, i) * toggle;
toggle = toggle * -1;
}
return ans;
}
public static void main(String[] args)
{
binomial();
double cosTheta = 0.5;
int n = 10;
System.out.println(String.format("%.5f",findCosnTheta(cosTheta, n)));
}
}
|
Python3
import math
MAX=16
nCr=[[0 for i in range(MAX)] for i in range(MAX)]
def binomial():
for i in range(MAX):
for j in range(0,i+1):
if j == 0 or j == i:
nCr[i][j] = 1
else:
nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1]
def findCosnTheta(cosTheta,n):
sinTheta = math.sqrt(1 - cosTheta * cosTheta)
ans = 0
toggle = 1
for i in range(0,n+1,2):
ans = ans + nCr[n][i]*(cosTheta**(n - i)) *(sinTheta**i) * toggle
toggle = toggle * -1
return ans
if __name__=='__main__':
binomial()
cosTheta = 0.5
n = 10
print(findCosnTheta(cosTheta, n))
|
C#
using System;
public class GFG{
static int MAX=16;
static int [,]nCr=new int[MAX,MAX];
static void binomial()
{
for (int i = 0; i < MAX; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i)
nCr[i,j] = 1;
else
nCr[i,j] = nCr[i - 1,j] + nCr[i - 1,j - 1];
}
}
}
static double findCosnTheta(double cosTheta, int n)
{
double sinTheta = Math.Sqrt(1 - cosTheta * cosTheta);
double ans = 0;
int toggle = 1;
for (int i = 0; i <= n; i += 2) {
ans = ans + nCr[n,i] * Math.Pow(cosTheta, n - i) *
Math.Pow(sinTheta, i) * toggle;
toggle = toggle * -1;
}
return ans;
}
public static void Main()
{
binomial();
double cosTheta = 0.5;
int n = 10;
Console.WriteLine(findCosnTheta(cosTheta, n));
}
}
|
Javascript
<script>
MAX = 16
var nCr = Array.from(Array(MAX), () => new Array(MAX));
function binomial()
{
for (var i = 0; i < MAX; i++) {
for (var j = 0; j <= i; j++) {
if (j == 0 || j == i)
nCr[i][j] = 1;
else
nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1];
}
}
}
function findCosnTheta(cosTheta, n)
{
var sinTheta = Math.sqrt(1 - cosTheta * cosTheta);
var ans = 0;
var toggle = 1;
for (var i = 0; i <= n; i += 2) {
ans = ans + nCr[n][i] * Math.pow(cosTheta, n - i) *
Math.pow(sinTheta, i) * toggle;
toggle = toggle * -1;
}
return ans.toFixed(1);
}
binomial();
var cosTheta = 0.5;
var n = 10;
document.write( findCosnTheta(cosTheta, n));
</script>
|
Time Complexity: O(MAX2)
Auxiliary Space: O(MAX2)
Share your thoughts in the comments
Please Login to comment...