Difference between Big O vs Big Theta Θ vs Big Omega Ω Notations
Last Updated :
11 Oct, 2023
Prerequisite – Asymptotic Notations, Properties of Asymptotic Notations, Analysis of Algorithms
1. Big O notation (O):
It is defined as upper bound and upper bound on an algorithm is the most amount of time required ( the worst case performance).
Big O notation is used to describe the asymptotic upper bound.
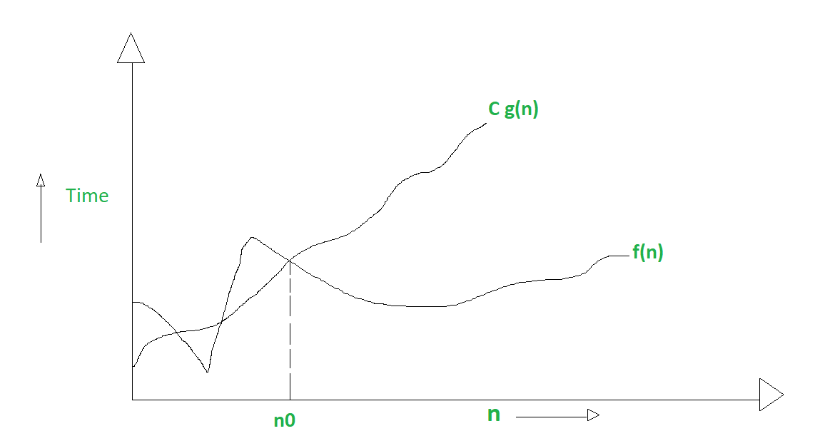
Mathematically, if f(n) describes the running time of an algorithm; f(n) is O(g(n)) if there exist positive constant C and n0 such that,
0 <= f(n) <= Cg(n) for all n >= n0
n = used to give upper bound a function.
If a function is O(n), it is automatically O(n-square) as well.
Graphic example for Big O :
2. Big Omega notation (Ω) :
It is define as lower bound and lower bound on an algorithm is the least amount of time required ( the most efficient way possible, in other words best case).
Just like O notation provide an asymptotic upper bound, Ω notation provides asymptotic lower bound.
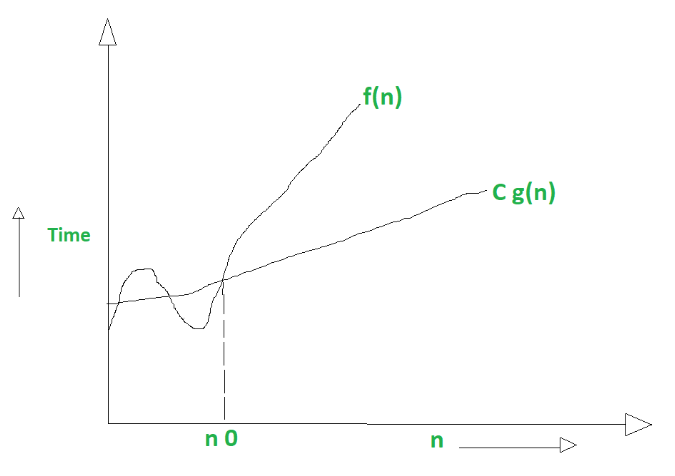
Let f(n) define running time of an algorithm;
f(n) is said to be Ω(g (n)) if there exists positive constant C and (n0) such that
0 <= Cg(n) <= f(n) for all n >= n0
n = used to given lower bound on a function
If a function is Ω(n-square) it is automatically Ω(n) as well.
Graphical example for Big Omega (Ω):
3. Big Theta notation (Θ) :
It is define as tightest bound and tightest bound is the best of all the worst case times that the algorithm can take.
Let f(n) define running time of an algorithm.
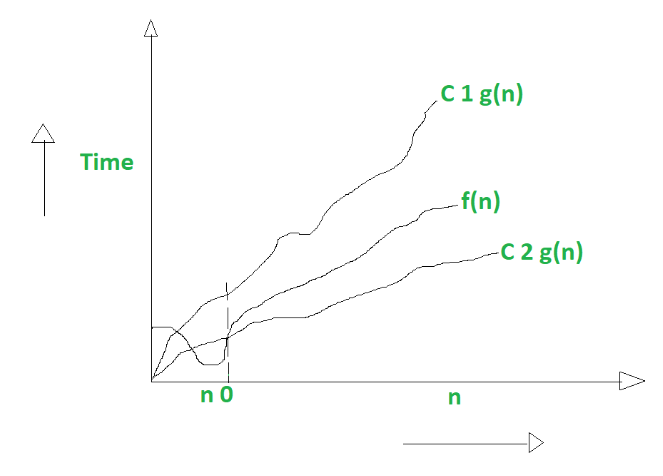
f(n) is said to be Θ(g(n)) if f(n) is O(g(n)) and f(n) is Ω(g(n)).
Mathematically,
0 <= f(n) <= C1g(n) for n >= n0
0 <= C2g(n) <= f(n) for n >= n0
Merging both the equation, we get :
0 <= C2g(n) <= f(n) <= C1g(n) for n >= n0
The equation simply means there exist positive constants C1 and C2 such that f(n) is sandwich between C2 g(n) and C1g(n).
Graphic example of Big Theta (Θ):
Difference Between Big oh, Big Omega and Big Theta :
It is like (<=)
rate of growth of an algorithm is less than or equal to a specific value. |
It is like (>=)
rate of growth is greater than or equal to a specified value. |
It is like (==)
meaning the rate of growth is equal to a specified value. |
| The upper bound of algorithm is represented by Big O notation. Only the above function is bounded by Big O. Asymptotic upper bound is given by Big O notation. |
The algorithm’s lower bound is represented by Omega notation. The asymptotic lower bound is given by Omega notation. |
The bounding of function from above and below is represented by theta notation. The exact asymptotic behavior is done by this theta notation. |
| Big O – Upper Bound |
Big Omega (Ω) – Lower Bound |
Big Theta (Θ) – Tight Bound |
| It is define as upper bound and upper bound on an algorithm is the most amount of time required ( the worst case performance). |
It is define as lower bound and lower bound on an algorithm is the least amount of time required ( the most efficient way possible, in other words best case). |
It is define as tightest bound and tightest bound is the best of all the worst case times that the algorithm can take. |
| Mathematically: Big Oh is 0 <= f(n) <= Cg(n) for all n >= n0 |
Mathematically: Big Omega is 0 <= Cg(n) <= f(n) for all n >= n0 |
Mathematically – Big Theta is 0 <= C2g(n) <= f(n) <= C1g(n) for n >= n0 |
For more details, please refer: Design and Analysis of Algorithms.
Share your thoughts in the comments
Please Login to comment...