Program to find Area of Triangle inscribed in N-sided Regular Polygon
Last Updated :
04 Jun, 2022
Given the triangle inscribed in an N-sided regular polygon with given side length, formed using any 3 vertices of the polygon, the task is to find the area of this triangle.
Examples:
Input: N = 6, side = 10
Output: 129.904
Input: N = 8, side = 5
Output: 45.2665
Approach: Consider the 1st example:
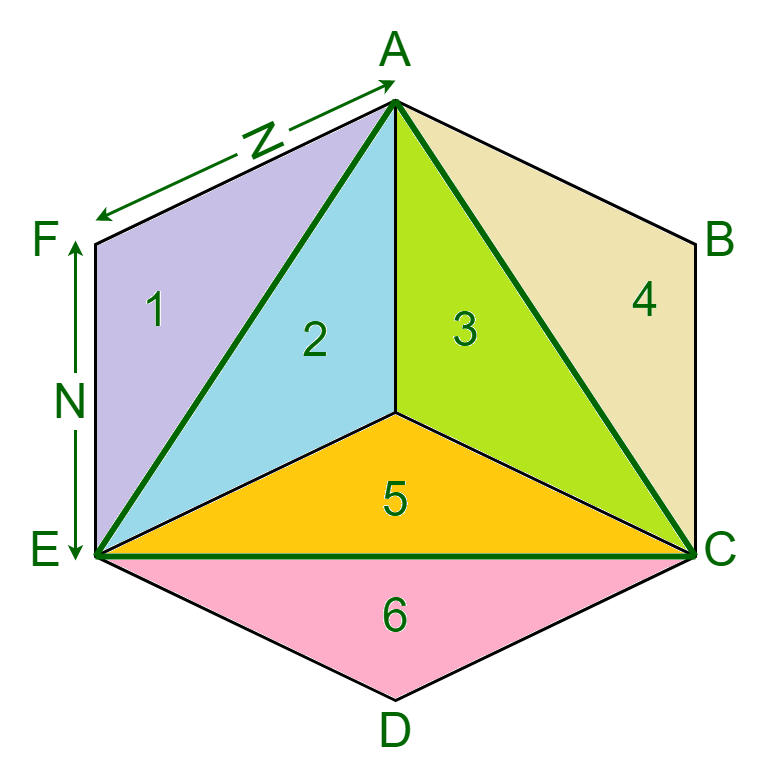
- Given is a 6 sided regular polygon ABCDEF with a triangle AEC inscribed in it.
- As it can be seen, the triangle divides given polygon into 6 equal triangular areas, where the point of intersection of triangle AEC is the centroid of the triangle.
- Find the area of the regular polygon. Area of the regular polygon can be calculated with the help of formula (A*P)/2 where P is the perimeter of that polygon and A is apothem of that polygon.
- Area of each of the triangulated part will be (TriangulatedArea = Area of N sided regular polygon / N) from the law of symmetry.
- Since the Triangle ACE comprises of 3 out of 6 in it, So the area of triangle ACE will be (3 * TriangulatedArea)
- Therefore, in general, if there is an N-sided regular polygon with area A, the area of a triangle inscribed in it will be (A/N)*3.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#include <cmath>
using namespace std;
double area_of_regular_polygon(double n, double len)
{
double P = (len * n);
double A
= len
/ (2 * tan((180 / n)
* 3.14159 / 180));
double area = (P * A) / 2;
return area;
}
double area_of_triangle_inscribed(double n, double len)
{
double area = area_of_regular_polygon(n, len);
double triangle = area / n;
double ins_tri = (triangle * 3);
return ins_tri;
}
int main()
{
double n = 6, len = 10;
cout << area_of_triangle_inscribed(n, len)
<< endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static double area_of_regular_polygon(double n,
double len)
{
double P = (len * n);
double A = len / (2 * Math.tan((180 / n) *
3.14159 / 180));
double area = (P * A) / 2;
return area;
}
static double area_of_triangle_inscribed(double n,
double len)
{
double area = area_of_regular_polygon(n, len);
double triangle = area / n;
double ins_tri = (triangle * 3);
return ins_tri;
}
static public void main(String[] arg)
{
double n = 6, len = 10;
System.out.printf("%.3f",
area_of_triangle_inscribed(n, len));
}
}
|
Python3
import math
def area_of_regular_polygon(n, len):
P = (len * n);
A = len / (2 * math.tan((180 / n) *
3.14159 / 180))
area = (P * A) / 2
return area
def area_of_triangle_inscribed(n, len):
area = area_of_regular_polygon(n, len)
triangle = area / n
ins_tri = (triangle * 3);
return ins_tri
n = 6
len = 10
print(round(area_of_triangle_inscribed(n, len), 3))
|
C#
using System;
class GFG
{
static double area_of_regular_polygon(double n,
double len)
{
double P = (len * n);
double A = len / (2 * Math.Tan((180 / n) *
3.14159 / 180));
double area = (P * A) / 2;
return area;
}
static double area_of_triangle_inscribed(double n,
double len)
{
double area = area_of_regular_polygon(n, len);
double triangle = area / n;
double ins_tri = (triangle * 3);
return ins_tri;
}
static public void Main(String[] arg)
{
double n = 6, len = 10;
Console.Write("{0:F3}",
area_of_triangle_inscribed(n, len));
}
}
|
Javascript
<script>
function area_of_regular_polygon(n, len)
{
let P = (len * n);
let A
= len
/ (2 * Math.tan((180 / n)
* 3.14159 / 180));
let area = (P * A) / 2;
return area;
}
function area_of_triangle_inscribed( n, len)
{
let area = area_of_regular_polygon(n, len);
let triangle = area / n;
let ins_tri = (triangle * 3);
return ins_tri;
}
let n = 6, len = 10;
document.write( area_of_triangle_inscribed(n, len).toFixed(3));
</script>
|
Time Complexity: O(1), the code will run in a constant time.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...