Count number of right triangles possible with a given perimeter
Last Updated :
08 Apr, 2023
Given a perimeter P, the task is to find the number of right triangles possible with perimeter equal to p.
Examples:
Input: P = 12
Output: number of right triangles = 1
The only right angle possible is with sides
hypotenuse = 5, perpendicular = 4 and base = 3.
Input: p = 840
Output: number of right triangles = 8
So the aim is to find the number of solutions which satisfy equations a + b + c = p and a2 + b2 = c2.
A naive approach is to run two loops for a(1 to p/2) and b(a+1 to p/3) then make c=p-a-b and increase count by one if 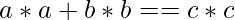 . This will take
. This will take 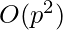 time.
time.
An efficient approach can be found by little algebraic manipulation :
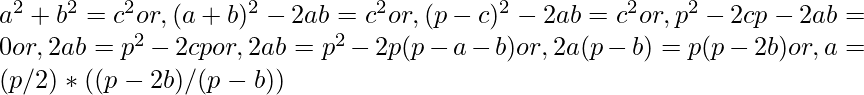
Since a + c > b or, p – b > b or, b < p/2. Thus iterating b from 1 to p/2, calculating a and storing only the whole number a would give all solutions for a given p. There are no right triangles are possible for odd p as right angle triangles follow the Pythagoras theorem. Use a list of pairs to store the values of a and band return the count at the end.
Below is the implementation of the above approach.
C++
#include<bits/stdc++.h>
using namespace std;
int countTriangles(int p)
{
vector<pair<int,int>> store;
if (p % 2 != 0)
return 0;
else
{
int count = 1;
for(int b = 1; b < p / 2; b++)
{
float a = (float)p / 2.0f * ((float)((float)p -
2.0 * (float)b) /
((float)p - (float)b));
int inta = (int)(a);
if (a == inta)
{
pair<int,int> ab;
if(inta<b)
{
ab = {inta, b};
}
else
{
ab = {b, inta};
}
if(find(store.begin(), store.end(), ab) == store.end())
{
count += 1;
store.push_back(ab);
}
}
}
return count;
}
}
int main()
{
int p = 840;
cout << "number of right triangles = " << countTriangles(p);
return 0;
}
|
Java
import java.util.*;
class Pair {
int first, second;
public Pair(int first, int second) {
this.first = first;
this.second = second;
}
}
class GFG {
static int countTriangles(int p) {
HashSet<Pair> store = new HashSet<Pair>();
if (p % 2 != 0)
return 0;
else {
int count = 1;
for(int b = 1; b < p / 3; b++) {
float a = (float)p / 2.0f * ((float)((float)p -
2.0 * (float)b) /
((float)p - (float)b));
int inta = (int)(a);
if (a == inta) {
Pair ab;
if(inta<b) {
ab = new Pair(inta, b);
} else {
ab = new Pair(b, inta);
}
if(!store.contains(ab) ) {
count += 1;
store.add(ab);
}
}
}
return count;
}
}
public static void main(String[] args) {
int p = 840;
System.out.print("number of right triangles = " + countTriangles(p));
}
}
|
Python3
def countTriangles(p):
store =[]
if p % 2 != 0 : return 0
else :
count = 0
for b in range(1, p // 2):
a = p / 2 * ((p - 2 * b) / (p - b))
inta = int(a)
if (a == inta ):
ab = tuple(sorted((inta, b)))
if ab not in store :
count += 1
store.append(ab)
return count
p = 840
print("number of right triangles = "+str(countTriangles(p)))
|
C#
using System;
using System.Collections.Generic;
public class GFG {
public class pair {
public int first, second;
public pair(int first, int second) {
this.first = first;
this.second = second;
}
}
static int countTriangles(int p)
{
HashSet<pair> store = new HashSet<pair>();
if (p % 2 != 0)
return 0;
else {
int count = 1;
for (int b = 1; b < p / 3; b++) {
float a = (float) p / 3 * ((float) ((float) p -
2 * (float) b) /
((float) p - (float) b));
int inta = (int) (a);
if (a == inta)
{
pair ab;
if (inta < b) {
ab = new pair(inta, b);
} else {
ab = new pair(b, inta);
}
if (!store.Contains(ab)) {
count += 1;
store.Add(ab);
}
}
}
return count;
}
}
public static void Main(String[] args) {
int p = 840;
Console.Write("number of right triangles = " + countTriangles(p));
}
}
|
Javascript
<script>
class pair {
constructor(first , second) {
this.first = first;
this.second = second;
}
}
function countTriangles(p)
{
var store = new Set();
if (p % 2 != 0)
return 0;
else {
var count = 1;
for (var b = 1; b < p / 3; b++) {
var a = p / 3 * ( ( p - 2 * b) / ( p - b));
var inta = parseInt( a);
if (a == inta) {
var ab;
if (inta < b) {
ab = new pair(inta, b);
} else {
ab = new pair(b, inta);
}
if (!store.has(ab)) {
count += 1;
store.add(ab);
}
}
}
return count;
}
}
var p = 840;
document.write("number of right triangles = " + countTriangles(p));
</script>
|
Output: number of right triangles = 8
Time complexity: O(P)
Space complexity: O(n) as auxiliary space is being used
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...