Program to calculate area of inner circle which passes through center of outer circle and touches its circumference
Last Updated :
13 Sep, 2023
Given a circle C1 and it’s a radius r1. And one another circle C2 whose passes through center of circle C1 and touch the circumference of circle C1. The task is to find out the area of circle C2.
Examples:
Input: r1 = 4
Output:Area of circle c2 = 12.56
Input: r1 = 7
Output:Area of circle c2 = 38.465
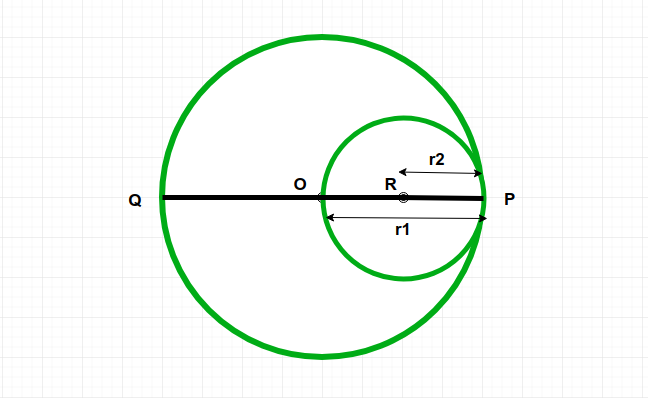
Approach:
Radius r2 of circle C2 is 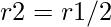 .
.
So we know that the area of circle is 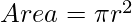 .
.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
#include <iostream>
using namespace std;
double innerCirclearea(double radius)
{
if (radius < 0)
{
return -1;
}
double r = radius / 2;
double Area = (3.14 * pow(r, 2));
return Area;
}
int main()
{
double radius = 4;
cout << ("Area of circle c2 = ",
innerCirclearea(radius));
return 0;
}
|
Java
class GFG {
static double innerCirclearea(double radius)
{
if (radius < 0) {
return -1;
}
double r = radius / 2;
double Area = (3.14 * Math.pow(r, 2));
return Area;
}
public static void main(String arr[])
{
double radius = 4;
System.out.println("Area of circle c2 = "
+ innerCirclearea(radius));
}
}
|
Python3
def innerCirclearea(radius) :
if (radius < 0) :
return -1;
r = radius / 2;
Area = (3.14 * pow(r, 2));
return Area;
if __name__ == "__main__" :
radius = 4;
print("Area of circle c2 =",
innerCirclearea(radius));
|
C#
using System;
class GFG
{
static double innerCirclearea(double radius)
{
if (radius < 0)
{
return -1;
}
double r = radius / 2;
double Area = (3.14 * Math.Pow(r, 2));
return Area;
}
public static void Main(String []arr)
{
double radius = 4;
Console.WriteLine("Area of circle c2 = " +
innerCirclearea(radius));
}
}
|
Javascript
function innerCircleArea(radius) {
if (radius < 0) {
return -1;
}
const r = radius / 2;
const area = 3.14 * Math.pow(r, 2);
return area;
}
const radius = 4;
console.log("Area of circle c2 = " + innerCircleArea(radius));
|
Time Complexity : O(log r)
Auxiliary Space : O(1) ,as we are not using any extra space.
Approach 2:
- Calculate the diameter of circle C1 by multiplying the radius r1 by 2.
- Calculate the radius r2 of circle C2 by dividing the diameter of C1 by 2.
- Calculate the area of circle C2 using the formula: Area = π * r2^2.
Below is the implementation of the above approach:
C++
#include <cmath>
#include <iomanip>
#include <iostream>
double calculateCircleArea(double radius)
{
if (radius < 0) {
return -1;
}
double radiusC2 = radius / 2;
double areaC2 = 3.14 * pow(radiusC2, 2);
return areaC2;
}
int main()
{
double radiusC1 = 4;
double areaC2 = calculateCircleArea(radiusC1);
std::cout << std::fixed << std::setprecision(2)
<< "Area of circle C2: " << areaC2
<< std::endl;
return 0;
}
|
Java
import java.util.Scanner;
public class Main {
static double calculateCircleArea(double radius)
{
if (radius < 0) {
return -1;
}
double r = radius / 2;
double area = (3.14 * Math.pow(r, 2));
return area;
}
public static void main(String[] args)
{
double radiusC1 = 4;
System.out.println("Area of circle C2: "
+ calculateCircleArea(radiusC1));
}
}
|
Python
import math
def calculate_circle_area(radius):
if radius < 0:
return -1
radius_c2 = radius / 2
area_c2 = 3.14 * math.pow(radius_c2, 2)
return area_c2
def main():
radius_c1 = 4
area_c2 = calculate_circle_area(radius_c1)
print("Area of circle C2: {:.2f}".format(area_c2))
if __name__ == "__main__":
main()
|
C#
using System;
class GFG {
static double CalculateCircleArea(double radius)
{
if (radius < 0) {
return -1;
}
double radiusC2 = radius / 2;
double areaC2 = 3.14 * Math.Pow(radiusC2, 2);
return areaC2;
}
static void Main()
{
double radiusC1 = 4;
double areaC2 = CalculateCircleArea(radiusC1);
Console.WriteLine("Area of circle C2: "
+ areaC2.ToString("F2"));
}
}
|
Javascript
function calculateCircleArea(radius) {
if (radius < 0) {
return -1;
}
const radiusC2 = radius / 2;
const areaC2 = 3.14 * Math.pow(radiusC2, 2);
return areaC2;
}
function main() {
const radiusC1 = 4;
const areaC2 = calculateCircleArea(radiusC1);
console.log(`Area of circle C2: ${areaC2.toFixed(2)}`);
return 0;
}
main();
|
OutputArea of circle C2: 12.56
Time Complexity : O(1)
Auxiliary Space : O(1)
Share your thoughts in the comments
Please Login to comment...