Find the equation of plane which passes through two points and parallel to a given axis
Last Updated :
27 Mar, 2022
Given two points A(x1, y1, z1) and B(x2, y2, z2) and a set of points (a, b, c) which represent the axis (ai + bj + ck), the task is to find the equation of plane which passes through the given points A and B and parallel to the given axis.
Examples:
Input: x1 = 1, y1 = 2, z1 = 3, x2 = 3, y2 = 4, z2 = 5, a= 6, b = 7, c = 8
Output: 2x + 4y + 2z + 0 = 0
Input: x1 = 2, y1 = 3, z1 = 5, x2 = 6, y2 = 7, z2 = 8, a= 11, b = 23, c = 10.
Output: -29x + 7y + 48z + 0= 0
Approach:
From the given two points on plane A and B, The directions ratios a vector equation of line AB is given by:
direction ratio = (x2 – x1, y2 – y1, z2 – z1)
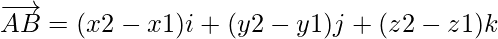
Since the line
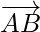
is parallel to the given axis
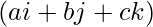
. Therefore, the cross-product of
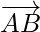
and
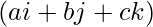
is 0 which is given by:
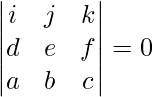
where,
d, e, and f are the coefficient of vector equation of line AB i.e.,
d = (x2 – x1),
e = (y2 – y1), and
f = (z2 – z1)
and a, b, and c are the coefficient of given axis.
The equation formed by the above determinant is given by:
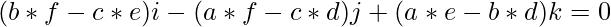
(Equation 1)
Equation 1 is perpendicular to the line AB which means it is perpendicular to the required plane.
Let the Equation of the plane is given by
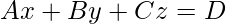
(Equation 2)
where A, B, and C are the direction ratio of the plane perpendicular to the plane.
Since Equation 1 is Equation 2 are perpendicular to each other, therefore the value of the direction ratio of Equation 1 & 2 are parallel. Then the coefficient of the plane is given by:
A = (b*f – c*e),
B = (a*f – c*d), and
C = (a*e – b*d)
Now dot product of plane and vector line AB gives the value of D as
D = -(A * d – B * e + C * f)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findEquation(int x1, int y1, int z1,
int x2, int y2, int z2,
int d, int e, int f)
{
double a = x2 - x1;
double b = y2 - y1;
double c = z2 - z1;
int A = (b * f - c * e);
int B = (a * f - c * d);
int C = (a * e - b * d);
int D = -(A * d - B * e + C * f);
cout << A << "x + " << B << "y + "
<< C << "z + " << D << "= 0";
}
int main()
{
int x1 = 2, y1 = 3, z1 = 5;
int x2 = 6, y2 = 7, z2 = 8;
int a = 11, b = 23, c = 10;
findEquation(x1, y1, z1,
x2, y2, z2,
a, b, c);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void findEquation(int x1, int y1, int z1,
int x2, int y2, int z2,
int d, int e, int f)
{
double a = x2 - x1;
double b = y2 - y1;
double c = z2 - z1;
int A = (int)(b * f - c * e);
int B = (int)(a * f - c * d);
int C = (int)(a * e - b * d);
int D = -(int)(A * d - B * e + C * f);
System.out.println(A + "x + " + B + "y + " +
C + "z + " + D + "= 0 ");
}
public static void main(String[] args)
{
int x1 = 2, y1 = 3, z1 = 5;
int x2 = 6, y2 = 7, z2 = 8;
int a = 11, b = 23, c = 10;
findEquation(x1, y1, z1,
x2, y2, z2,
a, b, c);
}
}
|
Python3
def findEquation(x1, y1, z1,
x2, y2, z2,
d, e, f):
a = x2 - x1
b = y2 - y1
c = z2 - z1
A = (b * f - c * e)
B = (a * f - c * d)
C = (a * e - b * d)
D = -(A * d - B *
e + C * f)
print (A, "x + ", B, "y + ",
C, "z + ", D, "= 0")
if __name__ == "__main__":
x1 = 2
y1 = 3
z1 = 5;
x2 = 6
y2 = 7
z2 = 8
a = 11
b = 23
c = 10
findEquation(x1, y1, z1,
x2, y2, z2,
a, b, c)
|
C#
using System;
class GFG{
static void findEquation(int x1, int y1, int z1,
int x2, int y2, int z2,
int d, int e, int f)
{
double a = x2 - x1;
double b = y2 - y1;
double c = z2 - z1;
int A = (int)(b * f - c * e);
int B = (int)(a * f - c * d);
int C = (int)(a * e - b * d);
int D = -(int)(A * d - B * e + C * f);
Console.Write(A + "x + " + B + "y + " +
C + "z + " + D + "= 0 ");
}
public static void Main()
{
int x1 = 2, y1 = 3, z1 = 5;
int x2 = 6, y2 = 7, z2 = 8;
int a = 11, b = 23, c = 10;
findEquation(x1, y1, z1,
x2, y2, z2,
a, b, c);
}
}
|
Javascript
<script>
function findEquation(x1 , y1 , z1 , x2 , y2 , z2 , d , e , f)
{
var a = x2 - x1;
var b = y2 - y1;
var c = z2 - z1;
var A = parseInt( (b * f - c * e));
var B = parseInt( (a * f - c * d));
var C = parseInt( (a * e - b * d));
var D = -parseInt( (A * d - B * e + C * f));
document.write(A + "x + " + B + "y + " + C + "z + " + D + "= 0 ");
}
var x1 = 2, y1 = 3, z1 = 5;
var x2 = 6, y2 = 7, z2 = 8;
var a = 11, b = 23, c = 10;
findEquation(x1, y1, z1, x2, y2, z2, a, b, c);
</script>
|
Output: -29x + 7y + 48z + 0= 0
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...