ML | Locally weighted Linear Regression
Last Updated :
13 Apr, 2023
Linear Regression is a supervised learning algorithm used for computing linear relationships between input (X) and output (Y). The steps involved in ordinary linear regression are:
Training phase: Compute 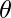 to minimize the cost.
to minimize the cost. 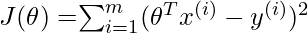
Predict output: for given query point 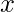 ,
, 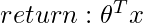

As evident from the image below, this algorithm cannot be used for making predictions when there exists a non-linear relationship between X and Y. In such cases, locally weighted linear regression is used.

Locally Weighted Linear Regression:
Locally weighted linear regression is a non-parametric algorithm, that is, the model does not learn a fixed set of parameters as is done in ordinary linear regression. Rather parameters 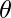 are computed individually for each query point
are computed individually for each query point 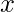 . While computing
. While computing 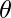 , a higher “preference” is given to the points in the training set lying in the vicinity of
, a higher “preference” is given to the points in the training set lying in the vicinity of 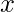 than the points lying far away from
than the points lying far away from 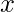 . The modified cost function is:
. The modified cost function is: 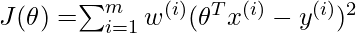 where,
where, 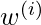 is a non-negative “weight” associated with training point
is a non-negative “weight” associated with training point 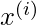 . For
. For 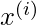 s lying closer to the query point
s lying closer to the query point 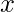 , the value of
, the value of 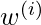 is large, while for
is large, while for 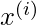 s lying far away from
s lying far away from 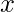 the value of
the value of 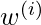 is small. A typical choice of
is small. A typical choice of 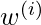 is:
is: 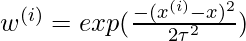 where
where 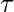 is called the bandwidth parameter and controls the rate at which
is called the bandwidth parameter and controls the rate at which 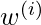 falls with distance from
falls with distance from 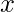 Clearly, if
Clearly, if  is small
is small 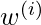 is close to 1 and if
is close to 1 and if  is large
is large 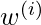 is close to 0. Thus, the training set points lying closer to the query point
is close to 0. Thus, the training set points lying closer to the query point 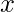 contribute more to the cost
contribute more to the cost  than the points lying far away from
than the points lying far away from 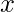 .
.
NOTE: For Locally Weighted Linear Regression, the data must always be available on the machine as it doesn’t learn from the whole set of data in a single shot. Whereas, in Linear Regression, after training the model the training set can be erased from the machine as the model has already learned the required parameters.
For example: Consider a query point 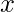 = 5.0 and let
= 5.0 and let 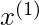 and
and  be two points in the training set such that
be two points in the training set such that 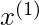 = 4.9 and
= 4.9 and  = 3.0. Using the formula
= 3.0. Using the formula 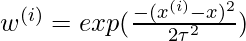 with
with 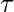 = 0.5:
= 0.5: 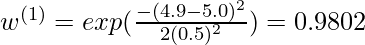 [Tex]w^{(2)} = exp(\frac{-(3.0 – 5.0)^2}{2(0.5)^2}) = 0.000335 [/Tex]
[Tex]w^{(2)} = exp(\frac{-(3.0 – 5.0)^2}{2(0.5)^2}) = 0.000335 [/Tex] Thus, the weights fall exponentially as the distance between
Thus, the weights fall exponentially as the distance between 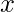 and
and 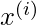 increases and so does the contribution of error in prediction for
increases and so does the contribution of error in prediction for 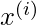 to the cost. Consequently, while computing
to the cost. Consequently, while computing 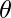 , we focus more on reducing
, we focus more on reducing 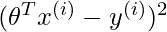 for the points lying closer to the query point (having a larger value of
for the points lying closer to the query point (having a larger value of 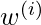 ).
).

Steps involved in locally weighted linear regression are:
Compute  to minimize the cost.
to minimize the cost. 
Predict Output: for given query point 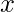 ,
, 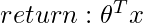
Points to remember:
- Locally weighted linear regression is a supervised learning algorithm.
- It is a non-parametric algorithm.
- There exists No training phase. All the work is done during the testing phase/while making predictions.
- The dataset must always be available for predictions.
- Locally weighted regression methods are a generalization of k-Nearest Neighbour.
- In Locally weighted regression an explicit local approximation is constructed from the target function for each query instance.
- The local approximation is based on the target function of the form like constant, linear, or quadratic functions localized kernel functions.
Share your thoughts in the comments
Please Login to comment...