Implementation of Locally Weighted Linear Regression
Last Updated :
12 Dec, 2021
LOESS or LOWESS are non-parametric regression methods that combine multiple regression models in a k-nearest-neighbor-based meta-model. LOESS combines much of the simplicity of linear least squares regression with the flexibility of nonlinear regression. It does this by fitting simple models to localized subsets of the data to build up a function that describes the variation in the data, point by point.
- This algorithm is used for making predictions when there exists a non-linear relationship between the features.
- Locally weighted linear regression is a supervised learning algorithm.
- It a non-parametric algorithm.
- doneThere exists No training phase. All the work is done during the testing phase/while making predictions.
Suppose we want to evaluate the hypothesis function h at a certain query point x. For linear regression we would do the following:
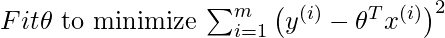
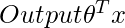
For locally weighted linear regression we will instead do the following:
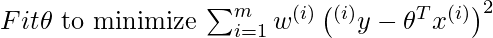
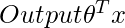
where w(i) is a is a non-negative “weight” associated with training point x(i). A higher “preference” is given to the points in the training set lying in the vicinity of x than the points lying far away from x. so For x(i) lying closer to the query point x, the value of w(i) is large, while for x(i) lying far away from x the value of w(i) is small.
w(i) can be chosen as –
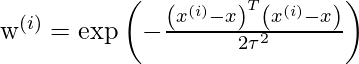
Directly using closed Form solution to find parameters-
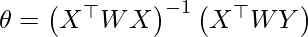
Code: Importing Libraries :
python
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.style.use("seaborn")
|
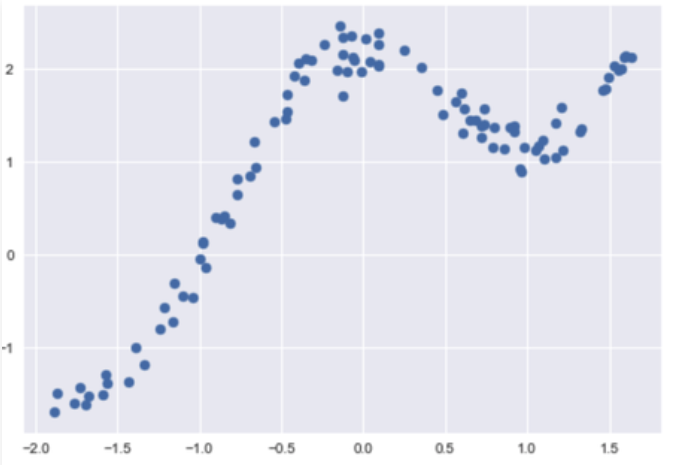
Code: Loading Data :
python
dfx = pd.read_csv('weightedX_LOWES.csv')
dfy = pd.read_csv('weightedY_LOWES.csv')
X = dfx.values
Y = dfy.values
|
Output:
Code: Function to calculate weight matrix :
python
def get_WeightMatrix_for_LOWES(query_point, Training_examples, Bandwidth):
M = Training_examples.shape[0]
W = np.mat(np.eye(M))
for i in range(M):
xi = Training_examples[i]
denominator = (-2 * Bandwidth * Bandwidth)
W[i, i] = np.exp(np.dot((xi-query_point), (xi-query_point).T)/denominator)
return W
|
Code: Making Predictions:
python
def predict(training_examples, Y, query_x, Bandwidth):
M = Training_examples.shape[0]
all_ones = np.ones((M, 1))
X_ = np.hstack((training_examples, all_ones))
qx = np.mat([query_x, 1])
W = get_WeightMatrix_for_LOWES(qx, X_, Bandwidth)
theta = np.linalg.pinv(X_.T*(W * X_))*(X_.T*(W * Y))
pred = np.dot(qx, theta)
return theta, pred
|
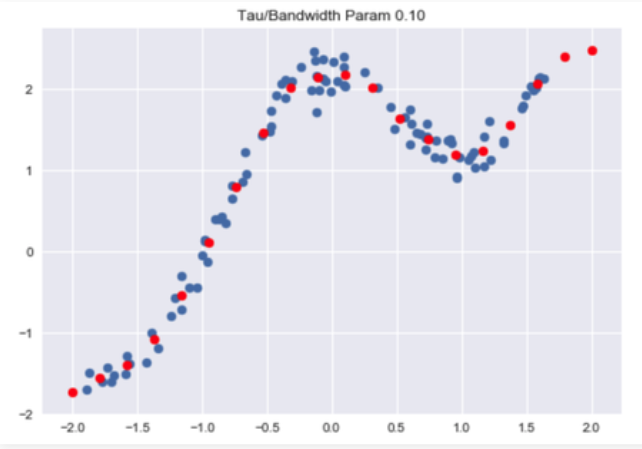
Code: Visualise Predictions :
python
Bandwidth = 0.1
X_test = np.linspace(-2, 2, 20)
Y_test = []
for query in X_test:
theta, pred = predict(X, Y, query, Bandwidth)
Y_test.append(pred[0][0])
horizontal_axis = np.array(X)
vertical_axis = np.array(Y)
plt.title("Tau / Bandwidth Param %.2f"% Bandwidth)
plt.scatter(horizontal_axis, vertical_axis)
Y_test = np.array(Y_test)
plt.scatter(X_test, Y_test, color ='red')
plt.show()
|
Share your thoughts in the comments
Please Login to comment...