Maximize sum of K corner elements in Array

Given an array arr[] and an integer K, the task is to find the maximize the sum of K elements in the Array by taking only corner elements.

A corner element is an element from the start of the array or from the end of the array.

Examples:

Input: arr[] = {8, 4, 4, 8, 12, 3, 2, 9}, K = 3 
Output: 21 
Explanation:
The optimal strategy is to pick the elements form the array is, two indexes from the beginning and one index from the end. All other possible choice will yield lesser sum. Hence, arr[0] + arr[1] + arr[7] = 21.

Input: arr[] = {2, 1, 14, 6, 4, 3}, K = 3 
Output: 17 
Explanation:
We will get the maximum sum by picking first three elements form the array. Hence, Optimal choice is: arr[0] + arr[1] + arr[2] = 17  

Naive Approach: The idea is to use Recursion. As we can only take a start or end index value hence initialize two variables and take exactly K steps and return the maximum sum among all the possible combinations. The recursive approach has exponential complexity due to its overlapping subproblem and optimal substructure property. 

Below is the implementation of the above approach:  

C++

// C++ program to maximize the sum of K elements
// in the array by taking only corner elements

#include <bits/stdc++.h>
using namespace std;

// Function to return maximum sum
int maxSum(int arr[], int K, int start, int end, int max_sum)
{
    // Base case
    if (K == 0)
        return max_sum;

    // Pick the start index
    int max_sum_start = max_sum + arr[start];

    // Pick the end index
    int max_sum_end = max_sum + arr[end];

    // Recursive function call
    int ans = max(
        maxSum(arr, K - 1, start + 1, end, max_sum_start),
        maxSum(arr, K - 1, start, end - 1, max_sum_end));

    // Return the final answer
    return ans;
}

// Function to find the maximized sum
void maximizeSum(int arr[], int K, int n)
{
    int max_sum = 0;
    int start = 0;
    int end = n - 1;
    cout << maxSum(arr, K, start, end, max_sum);
}

// Driver code
int main()
{
    int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = sizeof(arr) / sizeof(arr[0]);
    maximizeSum(arr, K, n);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

// C++ program to maximize the sum of K elements
// in the array by taking only corner elements

#include <stdio.h>

// Find maximum between two numbers.
int max(int num1, int num2)
{
    return (num1 > num2 ) ? num1 : num2;
}

// Function to return maximum sum
int maxSum(int arr[], int K, int start, int end, int max_sum)
{
    // Base case
    if (K == 0)
        return max_sum;

    // Pick the start index
    int max_sum_start = max_sum + arr[start];

    // Pick the end index
    int max_sum_end = max_sum + arr[end];

    // Recursive function call
    int ans = max(
        maxSum(arr, K - 1, start + 1, end, max_sum_start),
        maxSum(arr, K - 1, start, end - 1, max_sum_end));

    // Return the final answer
    return ans;
}

// Function to find the maximized sum
void maximizeSum(int arr[], int K, int n)
{
    int max_sum = 0;
    int start = 0;
    int end = n - 1;
    printf("%d",maxSum(arr, K, start, end, max_sum));
}

// Driver code
int main()
{
    int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = sizeof(arr) / sizeof(arr[0]);
    maximizeSum(arr, K, n);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java program to maximize the sum of K elements
// in the array by taking only corner elements
import java.util.*;

class GFG {

    // Function to return maximum sum
    static int maxSum(int arr[], int K, int start, int end, int max_sum)
    {
        // Base case
        if (K == 0)
            return max_sum;

        // Pick the start index
        int max_sum_start = max_sum + arr[start];

        // Pick the end index
        int max_sum_end = max_sum + arr[end];

        // Recursive function call
        int ans = Math.max(maxSum(arr, K - 1, start + 1, end, max_sum_start),
                           maxSum(arr, K - 1, start, end - 1, max_sum_end));

        // Return the final answer
        return ans;
    }

    // Function to find the maximized sum
    static void maximizeSum(int arr[], int K, int n)
    {
        int max_sum = 0;
        int start = 0;
        int end = n - 1;
        System.out.print(maxSum(arr, K, start, end, max_sum));
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
        int K = 3;
        int n = arr.length;
        maximizeSum(arr, K, n);
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 program to maximize the sum of K elements
# in the array by taking only corner elements

# Function to return maximum sum
def maxSum(arr, K, start, end, max_sum):

    # Base case
    if (K == 0):
        return max_sum

    # Pick the start index
    max_sum_start = max_sum + arr[start]

    # Pick the end index
    max_sum_end = max_sum + arr[end]

    # Recursive function call
    ans = max(maxSum(arr,  K - 1, start + 1,
                     end, max_sum_start),
          maxSum(arr, K - 1, start,
                     end - 1, max_sum_end))

    # Return the final answer
    return ans

# Function to find the maximized sum
def maximizeSum(arr, K, n):
    max_sum = 0
    start = 0
    end = n - 1

    print(maxSum(arr, K, start, end, max_sum))

# Driver code
if __name__ == '__main__':

    arr = [8, 4, 4, 8, 12, 3, 2, 9]
    K = 3
    n = len(arr)

    maximizeSum(arr, K, n)

# This code is contributed by Bhupendra_Singh

C#

// C# program to maximize the sum of K elements
// in the array by taking only corner elements
using System;

 class GFG{

// Function to return maximum sum
static int maxSum(int []arr, int K,
                  int start, int end,
                  int max_sum)
{
    // Base case
    if (K == 0)
        return max_sum;

    // Pick the start index
    int max_sum_start = max_sum + arr[start];

    // Pick the end index
    int max_sum_end = max_sum + arr[end];

    // Recursive function call
    int ans = Math.Max(maxSum(arr, K - 1, start + 1,
                              end, max_sum_start),
                       maxSum(arr, K - 1, start,
                              end - 1, max_sum_end));

    // Return the readonly answer
    return ans;
}

// Function to find the maximized sum
static void maximizeSum(int []arr, int K, int n)
{
    int max_sum = 0;
    int start = 0;
    int end = n - 1;
    Console.Write(maxSum(arr, K, start,
                         end, max_sum));
}

// Driver code
public static void Main(String[] args)
{
    int []arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = arr.Length;

    maximizeSum(arr, K, n);
}
}

// This code is contributed by sapnasingh4991

Javascript

<script>

// Javascript program to maximize the sum of K elements
// in the array by taking only corner elements

// Function to return maximum sum
function maxSum(arr, K,
                  start, end,
                  max_sum)
{
    // Base case
    if (K == 0)
        return max_sum;

    // Pick the start index
    let max_sum_start = max_sum + arr[start];

    // Pick the end index
    let max_sum_end = max_sum + arr[end];

    // Recursive function call
    let ans = Math.max(maxSum(arr, K - 1, start + 1,
                              end, max_sum_start),
                       maxSum(arr, K - 1, start,
                              end - 1, max_sum_end));

    // Return the final answer
    return ans;
}

// Function to find the maximized sum
function maximizeSum(arr, K, n)
{
    let max_sum = 0;
    let start = 0;
    let end = n - 1;
    document.write(maxSum(arr, K, start,
                            end, max_sum));
}
// Driver Code

    let arr = [ 8, 4, 4, 8, 12, 3, 2, 9 ];
    let K = 3;
    let n = arr.length;
    maximizeSum(arr, K, n);

</script>

Output:

21

Time Complexity: O(2^N)

Auxiliary Space: O(N)

Efficient Approach: To solve the problem more efficiently we will implement Sliding Window concept. 

• Initialize two integers with 0, curr_points and max_points to represents current points and maximum points respectively.
• Now, iterate over K elements one by one from the beginning and form the window of size K, also update the value of curr_points by curr_points + arr[i] and max_points with the value of curr_points.
• After that in each step, take one element from the end of the array and remove the rightmost element from the previously selected window with beginning elements where the window size always remains K. Update the values for curr_points and max_points accordingly. At last, we have K elements from the end of the array, and max_points contains the required result that has to be returned.

Let us look at the image below to understand it better:

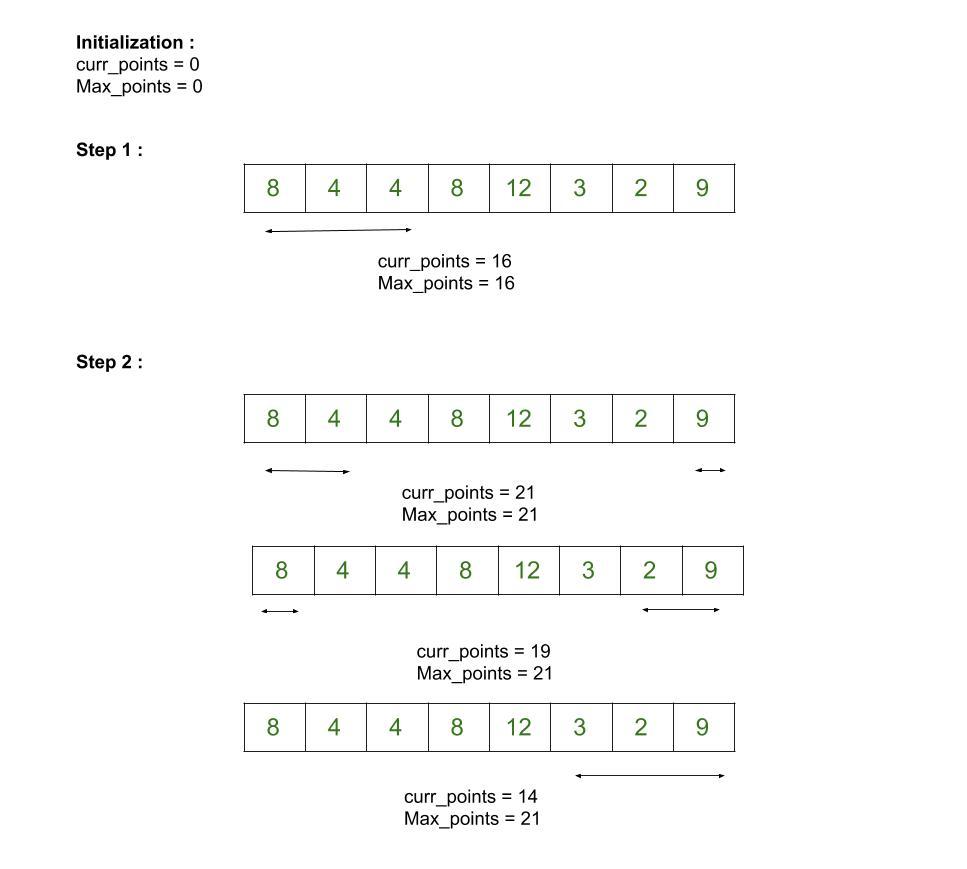
Below is the implementation of the above approach:

C++

// C++ program to maximize the sum of K elements
// in the array by taking only corner elements

#include <bits/stdc++.h>
using namespace std;

// Function to return maximum sum
int maxPointCount(int arr[], int K, int size)
{
    // Initialize variables
    int curr_points = 0;
    int max_points = 0;

    // Iterate over first K elements of array and update the
    // value for curr_points
    for (int i = 0; i < K; i++)
        curr_points += arr[i];

    // Update value for max_points
    max_points = curr_points;

    // j points to the end of the array
    int j = size - 1;
    for (int i = K - 1; i >= 0; i--) {
        curr_points = curr_points + arr[j] - arr[i];
        max_points = max(curr_points, max_points);
        j--;
    }
    // Return the final result
    return max_points;
}

// Driver code
int main()
{
    int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << maxPointCount(arr, K, n);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

// C program to maximize the sum of K elements
// in the array by taking only corner elements

#include <stdio.h>

// Find maximum between two numbers.
int max(int num1, int num2)
{
    return (num1 > num2 ) ? num1 : num2;
}

// Function to return maximum sum
int maxPointCount(int arr[], int K, int size)
{
    // Initialize variables
    int curr_points = 0;
    int max_points = 0;

    // Iterate over first K elements of array and update the
    // value for curr_points
    for (int i = 0; i < K; i++)
        curr_points += arr[i];

    // Update value for max_points
    max_points = curr_points;

    // j points to the end of the array
    int j = size - 1;
    for (int i = K - 1; i >= 0; i--) {
        curr_points = curr_points + arr[j] - arr[i];
        max_points = max(curr_points, max_points);
        j--;
    }
    // Return the final result
    return max_points;
}

// Driver code
int main()
{
    int arr[] = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("%d",maxPointCount(arr, K, n));
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java program to maximize the sum of K elements in the
// array by taking only corner elements
import java.util.Arrays;
import java.util.Scanner;

class GFG {

    // Function to return maximum sum
    public static int maxPointCount(int arr[], int K, int size)
    {
        // Initialize variables
        int curr_points = 0;
        int max_points = 0;
        // Iterate over first K elements of array and update
        // the value for curr_points
        for (int i = 0; i < K; i++)
            curr_points += arr[i];
        // Update value for max_points
        max_points = curr_points;
        // j points to the end of the array
        int j = size - 1;
        for (int i = K - 1; i >= 0; i--) {
            curr_points = curr_points + arr[j] - arr[i];
            max_points = Math.max(curr_points, max_points);
            j--;
        }
        // Return the final result
        return max_points;
    }

    // Driver code
    public static void main(String args[])
    {
        int[] arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
        int K = 3;
        int n = arr.length;
        System.out.print(maxPointCount(arr, K, n));
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 program to maximize the sum
# of K elements in the array by taking
# only corner elements

# Function to return maximum sum
def maxPointCount(arr, K, size):

    # Initialize variables
    curr_points = 0
    max_points = 0

    # Iterate over first K elements
    # of array and update the value
    # for curr_points
    for i in range(K):
        curr_points += arr[i]

    # Update value for max_points
    max_points = curr_points

    # j points to the end of the array
    j = size - 1

    for i in range(K - 1, -1, -1):
        curr_points = (curr_points +
                       arr[j] - arr[i])
        max_points = max(curr_points,
                         max_points)
        j -= 1

    # Return the final result
    return max_points

# Driver code
if __name__ == "__main__":

    arr = [ 8, 4, 4, 8, 12, 3, 2, 9 ]
    K = 3
    n = len(arr)

    print(maxPointCount(arr, K, n))

# This code is contributed by chitranayal

C#

// C# program to maximize the sum
// of K elements in the array by
// taking only corner elements
using System;
class GFG{

// Function to return maximum sum
public static int maxPointCount(int []arr,
                                int K,
                                int size)
{

    // Initialize variables
    int curr_points = 0;
    int max_points = 0;

    // Iterate over first K elements
    // of array and update the value
    // for curr_points
    for(int i = 0; i < K; i++)
        curr_points += arr[i];

    // Update value for max_points
    max_points = curr_points;

    // j points to the end of the array
    int j = size - 1;

    for(int i = K - 1; i >= 0; i--)
    {
        curr_points = curr_points +
                      arr[j] - arr[i];
        max_points = Math.Max(curr_points,
                              max_points);
        j--;
    }

    // Return the readonly result
    return max_points;
}

// Driver code
public static void Main(String []args)
{
    int []arr = { 8, 4, 4, 8, 12, 3, 2, 9 };
    int K = 3;
    int n = arr.Length;

    Console.Write( maxPointCount(arr, K, n));
}
}

// This code is contributed by sapnasingh4991

Javascript

<script>

// JavaScript program to maximize the sum
// of K elements in the array by
// taking only corner elements

// Function to return maximum sum
function maxPointCount(arr,k,size)
{
    // Initialize variables
    let curr_points = 0;
    let max_points = 0;

    // Iterate over first K elements
    // of array and update the value
    // for curr_points
    for(let i = 0; i < K; i++)
        curr_points += arr[i];

    // Update value for max_points
    max_points = curr_points;

    // j points to the end of the array
    let j = size - 1;

    for(let i = K - 1; i >= 0; i--)
    {
        curr_points = curr_points +
                      arr[j] - arr[i];
        max_points = Math.max(curr_points,
                              max_points);
        j--;
    }

    // Return the final result
    return max_points;
}

// Driver code
let arr=[8, 4, 4, 8, 12, 3, 2, 9];
let K = 3;
let n = arr.length;
document.write( maxPointCount(arr, K, n));


// This code is contributed by avanitrachhadiya2155

</script>

Output

21

Time Complexity: O(N), where N is size of the array.
Auxiliary Space Complexity: O(1).