Given two strings, S1 and S2, the task is to find the length of the Longest Common Subsequence, i.e. longest subsequence present in both of the strings.
A longest common subsequence (LCS) is defined as the longest subsequence which is common in all given input sequences.
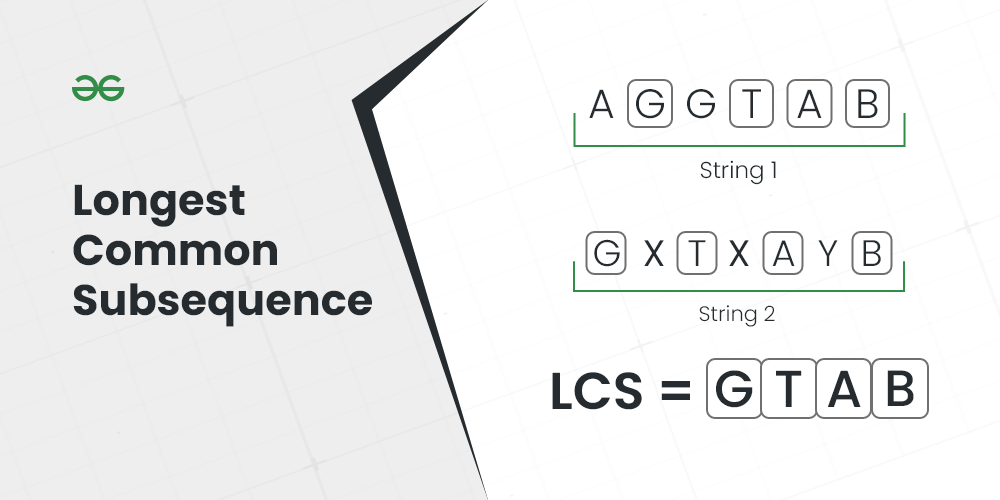
Longest Common Subsequence
Examples:
Input: S1 = “AGGTAB”, S2 = “GXTXAYB”
Output: 4
Explanation: The longest subsequence which is present in both strings is “GTAB”.
Input: S1 = “BD”, S2 = “ABCD”
Output: 2
Explanation: The longest subsequence which is present in both strings is “BD”.
Longest Common Subsequence (LCS) using Recursion:
Generate all the possible subsequences and find the longest among them that is present in both strings using recursion.
Follow the below steps to implement the idea:
- Create a recursive function [say lcs()].
- Check the relation between the First characters of the strings that are not yet processed.
- Depending on the relation call the next recursive function as mentioned above.
- Return the length of the LCS received as the answer.
Below is the implementation of the recursive approach:
C++
#include <bits/stdc++.h>
using namespace std;
int lcs(string X, string Y, int m, int n)
{
if (m == 0 || n == 0)
return 0;
if (X[m - 1] == Y[n - 1])
return 1 + lcs(X, Y, m - 1, n - 1);
else
return max(lcs(X, Y, m, n - 1),
lcs(X, Y, m - 1, n));
}
int main()
{
string S1 = "AGGTAB";
string S2 = "GXTXAYB";
int m = S1.size();
int n = S2.size();
cout << "Length of LCS is " << lcs(S1, S2, m, n);
return 0;
}
|
C
#include <stdio.h>
int max(int a, int b);
int lcs(char* X, char* Y, int i, int j)
{
if (X[i] == 0 || Y[j] == 0)
return 0;
if (X[i] == Y[j])
return 1 + lcs(X, Y, i + 1, j + 1);
else
return max(lcs(X, Y, i, j + 1),
lcs(X, Y, i + 1, j));
}
int max(int a, int b) { return (a > b) ? a : b; }
int main()
{
char S1[] = "BD";
char S2[] = "ABCD";
int m = strlen(S1);
int n = strlen(S2);
int i = 0, j = 0;
printf("Length of LCS is %d", lcs(S1, S2, i, j));
return 0;
}
|
Java
import java.io.*;
import java.util.*;
public class LongestCommonSubsequence {
int lcs(String X, String Y, int m, int n)
{
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + lcs(X, Y, m - 1, n - 1);
else
return max(lcs(X, Y, m, n - 1),
lcs(X, Y, m - 1, n));
}
int max(int a, int b) { return (a > b) ? a : b; }
public static void main(String[] args)
{
LongestCommonSubsequence lcs
= new LongestCommonSubsequence();
String S1 = "AGGTAB";
String S2 = "GXTXAYB";
int m = S1.length();
int n = S2.length();
System.out.println("Length of LCS is"
+ " " + lcs.lcs(S1, S2, m, n));
}
}
|
Python3
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1)
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
if __name__ == '__main__':
S1 = "AGGTAB"
S2 = "GXTXAYB"
print("Length of LCS is", lcs(S1, S2, len(S1), len(S2)))
|
C#
using System;
class GFG {
static int lcs(String X, String Y, int m, int n)
{
if (m == 0 || n == 0)
return 0;
if (X[m - 1] == Y[n - 1])
return 1 + lcs(X, Y, m - 1, n - 1);
else
return max(lcs(X, Y, m, n - 1),
lcs(X, Y, m - 1, n));
}
static int max(int a, int b) { return (a > b) ? a : b; }
public static void Main()
{
String S1 = "AGGTAB";
String S2 = "GXTXAYB";
int m = S1.Length;
int n = S2.Length;
Console.Write("Length of LCS is"
+ " " + lcs(S1, S2, m, n));
}
}
|
Javascript
<script>
function lcs( X, Y , m , n )
{
if (m == 0 || n == 0)
return 0;
if (X[m-1] == Y[n-1])
return 1 + lcs(X, Y, m-1, n-1);
else
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}
function max(a , b)
{
return (a > b)? a : b;
}
var s1 = "AGGTAB";
var s2 = "GXTXAYB";
var X = s1;
var Y = s2;
var m = X.length;
var n = Y.length;
document.write("Length of LCS is" + " " +
lcs( X, Y, m, n ) );
</script>
|
PHP
<?php
function lcs($X, $Y, $m, $n)
{
if($m == 0 || $n == 0)
return 0;
else if ($X[$m - 1] == $Y[$n - 1])
return 1 + lcs($X, $Y,
$m - 1, $n - 1);
else
return max(lcs($X, $Y, $m, $n - 1),
lcs($X, $Y, $m - 1, $n));
}
$S1 = "AGGTAB";
$S2 = "GXTXAYB";
echo "Length of LCS is ";
echo lcs($S1 , $S2, strlen($S1),
strlen($S2));
?>
|
Output
Length of LCS is 4
Time Complexity: O(2m*n)
Auxiliary Space: O(1)
Longest Common Subsequence (LCS) using Memoization:
If we notice carefully, we can observe that the above recursive solution holds the following two properties:
1. Optimal Substructure:
See for solving the structure of L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) we are taking the help of the substructures of X[0, 1, …, m-2], Y[0, 1,…, n-2], depending on the situation (i.e., using them optimally) to find the solution of the whole.
2. Overlapping Subproblems:
If we use the above recursive approach for strings “BD” and “ABCD“, we will get a partial recursion tree as shown below. Here we can see that the subproblem L(“BD”, “ABCD”) is being calculated more than once. If the total tree is considered there will be several such overlapping subproblems.
L(“AXYT”, “AYZX”)
/ \
L(“AXY”, “AYZX”) L(“AXYT”, “AYZ”)
/ \ / \
L(“AX”, “AYZX”) L(“AXY”, “AYZ”) L(“AXY”, “AYZ”) L(“AXYT”, “AY”)
Approach: Because of the presence of these two properties we can use Dynamic programming or Memoization to solve the problem. Below is the approach for the solution using recursion.
- Create a recursive function. Also create a 2D array to store the result of a unique state.
- During the recursion call, if the same state is called more than once, then we can directly return the answer stored for that state instead of calculating again.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int lcs(char* X, char* Y, int m, int n,
vector<vector<int> >& dp)
{
if (m == 0 || n == 0)
return 0;
if (X[m - 1] == Y[n - 1])
return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);
if (dp[m][n] != -1) {
return dp[m][n];
}
return dp[m][n] = max(lcs(X, Y, m, n - 1, dp),
lcs(X, Y, m - 1, n, dp));
}
int main()
{
char X[] = "AGGTAB";
char Y[] = "GXTXAYB";
int m = strlen(X);
int n = strlen(Y);
vector<vector<int> > dp(m + 1, vector<int>(n + 1, -1));
cout << "Length of LCS is " << lcs(X, Y, m, n, dp);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int lcs(String X, String Y, int m, int n,
int[][] dp)
{
if (m == 0 || n == 0)
return 0;
if (dp[m][n] != -1)
return dp[m][n];
if (X.charAt(m - 1) == Y.charAt(n - 1)) {
dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);
return dp[m][n];
}
dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),
lcs(X, Y, m - 1, n, dp));
return dp[m][n];
}
public static void main(String args[])
{
String X = "AGGTAB";
String Y = "GXTXAYB";
int m = X.length();
int n = Y.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i < m + 1; i++) {
for (int j = 0; j < n + 1; j++) {
dp[i][j] = -1;
}
}
System.out.println("Length of LCS is "
+ lcs(X, Y, m, n, dp));
}
}
|
Python3
def lcs(X, Y, m, n, dp):
if (m == 0 or n == 0):
return 0
if (dp[m][n] != -1):
return dp[m][n]
if X[m - 1] == Y[n - 1]:
dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp)
return dp[m][n]
dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp))
return dp[m][n]
X = "AGGTAB"
Y = "GXTXAYB"
m = len(X)
n = len(Y)
dp = [[-1 for i in range(n + 1)]for j in range(m + 1)]
print(f"Length of LCS is {lcs(X, Y, m, n, dp)}")
|
C#
using System;
class GFG {
static int lcs(char[] X, char[] Y, int m, int n,
int[, ] L)
{
if (m == 0 || n == 0)
return 0;
if (L[m, n] != -1)
return L[m, n];
if (X[m - 1] == Y[n - 1]) {
L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);
return L[m, n];
}
L[m, n] = max(lcs(X, Y, m, n - 1, L),
lcs(X, Y, m - 1, n, L));
return L[m, n];
}
static int max(int a, int b) { return (a > b) ? a : b; }
public static void Main()
{
String s1 = "AGGTAB";
String s2 = "GXTXAYB";
char[] X = s1.ToCharArray();
char[] Y = s2.ToCharArray();
int m = X.Length;
int n = Y.Length;
int[, ] L = new int[m + 1, n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
L[i, j] = -1;
}
}
Console.Write("Length of LCS is"
+ " " + lcs(X, Y, m, n, L));
}
}
|
Javascript
function lcs(X, Y, m, n, dp)
{
if (m == 0 || n == 0)
return 0;
if (X[m - 1] == Y[n - 1])
return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);
if (dp[m][n] != -1) {
return dp[m][n];
}
return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),
lcs(X, Y, m - 1, n, dp));
}
let X = "AGGTAB";
let Y = "GXTXAYB";
let m = X.length;
let n = Y.length;
let dp = new Array(m + 1);
for(let i = 0; i < m + 1; i++)
{
dp[i] = new Array(n + 1).fill(-1);
}
console.log("Length of LCS is " + lcs(X, Y, m, n, dp));
|
Output
Length of LCS is 4
Time Complexity: O(m * n) where m and n are the string lengths.
Auxiliary Space: O(m * n) Here the recursive stack space is ignored.
Longest Common Subsequence (LCS) using Bottom-Up (Tabulation):
We can use the following steps to implement the dynamic programming approach for LCS.
- Create a 2D array dp[][] with rows and columns equal to the length of each input string plus 1 [the number of rows indicates the indices of S1 and the columns indicate the indices of S2].
- Initialize the first row and column of the dp array to 0.
- Iterate through the rows of the dp array, starting from 1 (say using iterator i).
- For each i, iterate all the columns from j = 1 to n:
- If S1[i-1] is equal to S2[j-1], set the current element of the dp array to the value of the element to (dp[i-1][j-1] + 1).
- Else, set the current element of the dp array to the maximum value of dp[i-1][j] and dp[i][j-1].
- After the nested loops, the last element of the dp array will contain the length of the LCS.
See the below illustration for a better understanding:
Illustration:
Say the strings are S1 = “AGGTAB” and S2 = “GXTXAYB”.
First step: Initially create a 2D matrix (say dp[][]) of size 8 x 7 whose first row and first column are filled with 0.
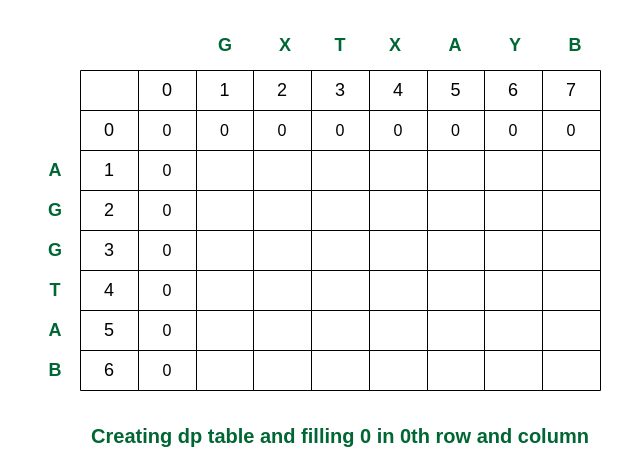
Creating the dp table
Second step: Traverse for i = 1. When j becomes 5, S1[0] and S2[4] are equal. So the dp[][] is updated. For the other elements take the maximum of dp[i-1][j] and dp[i][j-1]. (In this case, if both values are equal, we have used arrows to the previous rows).
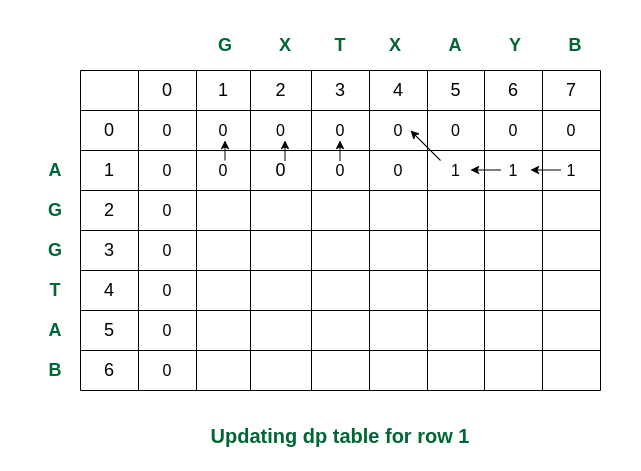
Filling the row no 1
Third step: While traversed for i = 2, S1[1] and S2[0] are the same (both are ‘G’). So the dp value in that cell is updated. Rest of the elements are updated as per the conditions.
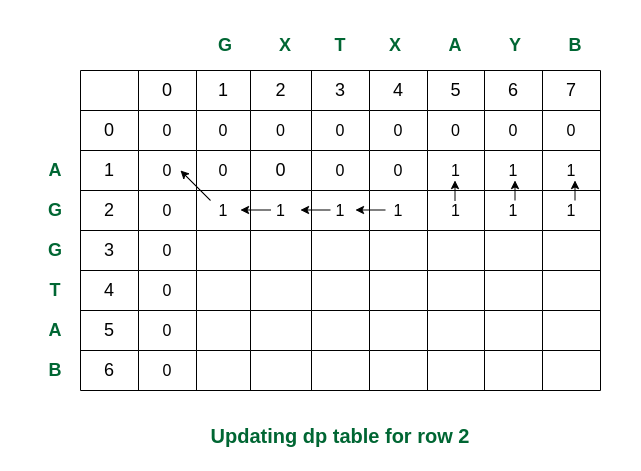
Filling the row no. 2
Fourth step: For i = 3, S1[2] and S2[0] are again same. The updations are as follows.
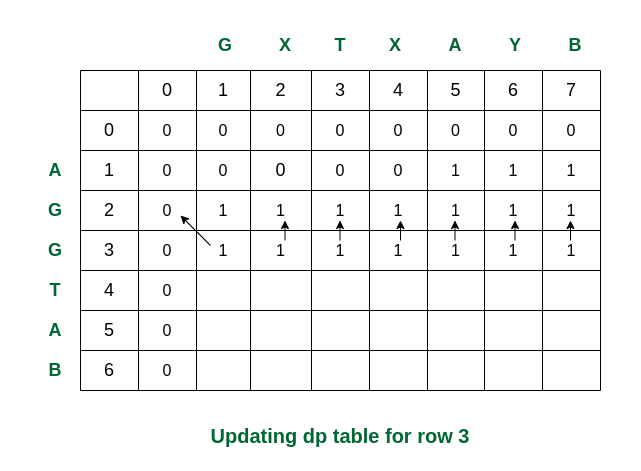
Filling row no. 3
Fifth step: For i = 4, we can see that S1[3] and S2[2] are same. So dp[4][3] updated as dp[3][2] + 1 = 2.
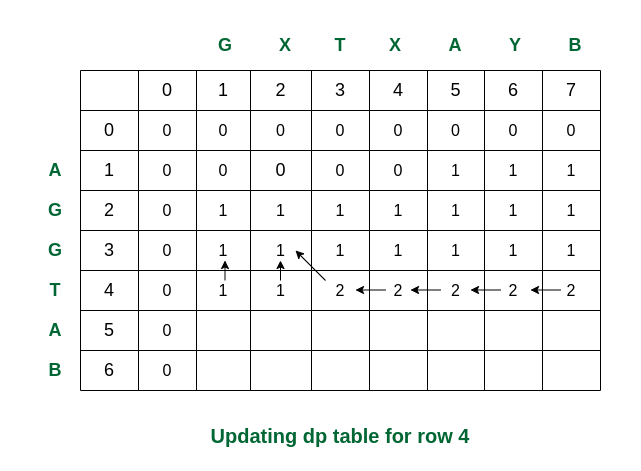
Filling row 4
Sixth step: Here we can see that for i = 5 and j = 5 the values of S1[4] and S2[4] are same (i.e., both are ‘A’). So dp[5][5] is updated accordingly and becomes 3.
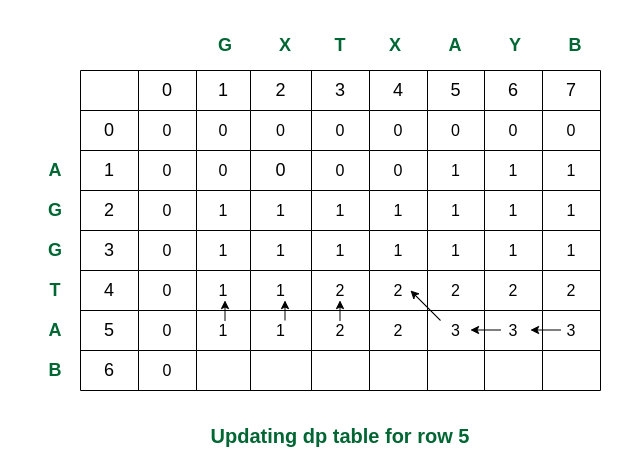
Filling row 5
Final step: For i = 6, see the last characters of both strings are same (they are ‘B’). Therefore the value of dp[6][7] becomes 4.
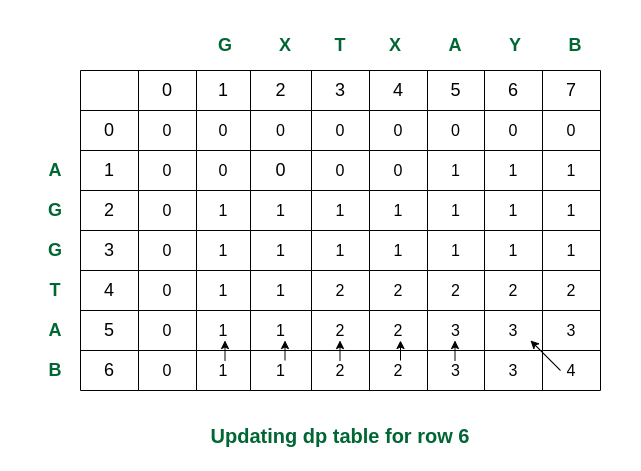
Filling the final row
So we get the maximum length of common subsequence as 4.
Following is a tabulated implementation for the LCS problem.
C++
#include <bits/stdc++.h>
using namespace std;
int lcs(string X, string Y, int m, int n)
{
int L[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X[i - 1] == Y[j - 1])
L[i][j] = L[i - 1][j - 1] + 1;
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
return L[m][n];
}
int main()
{
string S1 = "AGGTAB";
string S2 = "GXTXAYB";
int m = S1.size();
int n = S2.size();
cout << "Length of LCS is " << lcs(S1, S2, m, n);
return 0;
}
|
Java
import java.util.*;
public class LongestCommonSubsequence {
int lcs(String X, String Y, int m, int n)
{
int L[][] = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X.charAt(i - 1) == Y.charAt(j - 1))
L[i][j] = L[i - 1][j - 1] + 1;
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
return L[m][n];
}
int max(int a, int b) { return (a > b) ? a : b; }
public static void main(String[] args)
{
LongestCommonSubsequence lcs
= new LongestCommonSubsequence();
String S1 = "AGGTAB";
String S2 = "GXTXAYB";
int m = S1.length();
int n = S2.length();
System.out.println("Length of LCS is"
+ " " + lcs.lcs(S1, S2, m, n));
}
}
|
Python3
def lcs(X, Y, m, n):
L = [[None]*(n+1) for i in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if i == 0 or j == 0:
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1]+1
else:
L[i][j] = max(L[i-1][j], L[i][j-1])
return L[m][n]
if __name__ == '__main__':
S1 = "AGGTAB"
S2 = "GXTXAYB"
m = len(S1)
n = len(S2)
print("Length of LCS is", lcs(S1, S2, m, n))
|
C#
using System;
class GFG {
static int lcs(String X, String Y, int m, int n)
{
int[, ] L = new int[m + 1, n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[i, j] = 0;
else if (X[i - 1] == Y[j - 1])
L[i, j] = L[i - 1, j - 1] + 1;
else
L[i, j] = max(L[i - 1, j], L[i, j - 1]);
}
}
return L[m, n];
}
static int max(int a, int b) { return (a > b) ? a : b; }
public static void Main()
{
String S1 = "AGGTAB";
String S2 = "GXTXAYB";
int m = S1.Length;
int n = S2.Length;
Console.Write("Length of LCS is"
+ " " + lcs(S1, S2, m, n));
}
}
|
Javascript
<script>
function max(a, b)
{
if (a > b)
return a;
else
return b;
}
function lcs(X, Y, m, n)
{
var L = new Array(m + 1);
for(var i = 0; i < L.length; i++)
{
L[i] = new Array(n + 1);
}
var i, j;
for(i = 0; i <= m; i++)
{
for(j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
L[i][j] = 0;
else if (X[i - 1] == Y[j - 1])
L[i][j] = L[i - 1][j - 1] + 1;
else
L[i][j] = max(L[i - 1][j], L[i][j - 1]);
}
}
return L[m][n];
}
var S1 = "AGGTAB";
var S2 = "GXTXAYB";
var m = S1.length;
var n = S2.length;
document.write("Length of LCS is " + lcs(S1, S2, m, n));
</script>
|
PHP
<?php
function lcs($X , $Y, $m, $n)
{
for ($i = 0; $i <= $m; $i++)
{
for ($j = 0; $j <= $n; $j++)
{
if ($i == 0 || $j == 0)
$L[$i][$j] = 0;
else if ($X[$i - 1] == $Y[$j - 1])
$L[$i][$j] = $L[$i - 1][$j - 1] + 1;
else
$L[$i][$j] = max($L[$i - 1][$j],
$L[$i][$j - 1]);
}
}
return $L[$m][$n];
}
$S1 = "AGGTAB";
$S2 = "GXTXAYB";
$m = strlen($S1);
$n = strlen($S2) ;
echo "Length of LCS is ";
echo lcs($S1, $S2, $m, $n);
?>
|
Output
Length of LCS is 4
Time Complexity: O(m * n) which is much better than the worst-case time complexity of Naive Recursive implementation.
Auxiliary Space: O(m * n) because the algorithm uses an array of size (m+1)*(n+1) to store the length of the common substrings.
Longest Common Subsequence (LCS) using Bottom-Up (Space-Optimization):
- In the above tabulation approach we are using L[i-1][j] and L[i][j] etc, here the L[i-1] will refers to the matrix L’s previous row and L[i] refers to the current row.
- We can do space optimization by using two vectors one is previous and another one is current.
- When the inner for loop exits we are initializing previous equal to current.
Below is the implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int longestCommonSubsequence(string& text1, string& text2)
{
int n = text1.size();
int m = text2.size();
vector<int> prev(m + 1, 0), cur(m + 1, 0);
for (int idx2 = 0; idx2 < m + 1; idx2++)
cur[idx2] = 0;
for (int idx1 = 1; idx1 < n + 1; idx1++) {
for (int idx2 = 1; idx2 < m + 1; idx2++) {
if (text1[idx1 - 1] == text2[idx2 - 1])
cur[idx2] = 1 + prev[idx2 - 1];
else
cur[idx2]
= 0 + max(cur[idx2 - 1], prev[idx2]);
}
prev = cur;
}
return cur[m];
}
int main()
{
string S1 = "AGGTAB";
string S2 = "GXTXAYB";
cout << "Length of LCS is "
<< longestCommonSubsequence(S1, S2);
return 0;
}
|
Java
import java.util.Arrays;
public class GFG {
public static int longestCommonSubsequence(String text1, String text2) {
int n = text1.length();
int m = text2.length();
int[] prev = new int[m + 1];
int[] cur = new int[m + 1];
for (int idx1 = 1; idx1 < n + 1; idx1++) {
for (int idx2 = 1; idx2 < m + 1; idx2++) {
if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))
cur[idx2] = 1 + prev[idx2 - 1];
else
cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);
}
prev = Arrays.copyOf(cur, m + 1);
}
return cur[m];
}
public static void main(String[] args) {
String S1 = "AGGTAB";
String S2 = "GXTXAYB";
System.out.println("Length of LCS is " + longestCommonSubsequence(S1, S2));
}
}
|
Python3
def longestCommonSubsequence(text1, text2):
n = len(text1)
m = len(text2)
prev = [0] * (m + 1)
cur = [0] * (m + 1)
for idx1 in range(1, n + 1):
for idx2 in range(1, m + 1):
if text1[idx1 - 1] == text2[idx2 - 1]:
cur[idx2] = 1 + prev[idx2 - 1]
else:
cur[idx2] = max(cur[idx2 - 1], prev[idx2])
prev = cur.copy()
return cur[m]
if __name__ == '__main__':
S1 = "AGGTAB"
S2 = "GXTXAYB"
print("Length of LCS is", longestCommonSubsequence(S1, S2))
|
C#
using System;
class Program
{
static int LongestCommonSubsequence(string text1, string text2)
{
int n = text1.Length;
int m = text2.Length;
int[] prev = new int[m + 1];
int[] cur = new int[m + 1];
for (int idx2 = 0; idx2 < m + 1; idx2++)
cur[idx2] = 0;
for (int idx1 = 1; idx1 < n + 1; idx1++)
{
for (int idx2 = 1; idx2 < m + 1; idx2++)
{
if (text1[idx1 - 1] == text2[idx2 - 1])
cur[idx2] = 1 + prev[idx2 - 1];
else
cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);
}
prev = cur;
}
return cur[m];
}
static void Main()
{
string S1 = "AGGTAB";
string S2 = "GXTXAYB";
Console.WriteLine("Length of LCS is " + LongestCommonSubsequence(S1, S2));
}
}
|
Javascript
function longestCommonSubsequence(text1, text2) {
const n = text1.length;
const m = text2.length;
let prev = new Array(m + 1).fill(0);
let cur = new Array(m + 1).fill(0);
for (let idx2 = 0; idx2 < m + 1; idx2++) {
cur[idx2] = 0;
}
for (let idx1 = 1; idx1 < n + 1; idx1++) {
for (let idx2 = 1; idx2 < m + 1; idx2++) {
if (text1[idx1 - 1] === text2[idx2 - 1]) {
cur[idx2] = 1 + prev[idx2 - 1];
}
else {
cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);
}
}
prev = [...cur];
}
return cur[m];
}
function main() {
const S1 = "AGGTAB";
const S2 = "GXTXAYB";
console.log("Length of LCS is " + longestCommonSubsequence(S1, S2));
}
main();
|
Output
Length of LCS is 4
Time Complexity: O(m * n), which remains the same.
Auxiliary Space: O(m) because the algorithm uses two arrays of size m.
Feeling lost in the world of random DSA topics, wasting time without progress? It's time for a change! Join our DSA course, where we'll guide you on an exciting journey to master DSA efficiently and on schedule.
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 geeks!
Last Updated :
05 Oct, 2023
Like Article
Save Article