Find if an array of strings can be chained to form a circle | Set 2
Last Updated :
11 Mar, 2024
Given an array of strings, find if the given strings can be chained to form a circle. A string X can be put before another string Y in a circle if the last character of X is the same as the first character of Y.
Examples:
Input: arr[] = {"geek", "king"}
Output: Yes, the given strings can be chained.
Note that the last character of first string is same
as first character of second string and vice versa is
also true.
Input: arr[] = {"for", "geek", "rig", "kaf"}
Output: Yes, the given strings can be chained.
The strings can be chained as "for", "rig", "geek"
and "kaf"
Input: arr[] = {"aab", "bac", "aaa", "cda"}
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bac"
and "cda"
Input: arr[] = {"aaa", "bbb", "baa", "aab"};
Output: Yes, the given strings can be chained.
The strings can be chained as "aaa", "aab", "bbb"
and "baa"
Input: arr[] = {"aaa"};
Output: Yes
Input: arr[] = {"aaa", "bbb"};
Output: No
Input : arr[] = ["abc", "efg", "cde", "ghi", "ija"]
Output : Yes
These strings can be reordered as, “abc”, “cde”, “efg”,
“ghi”, “ija”
Input : arr[] = [“ijk”, “kji”, “abc”, “cba”]
Output : No
We strongly recommend that you practice it, before moving on to the solution.
We have discussed one approach to this problem in the below post.
Find if an array of strings can be chained to form a circle | Set 1
In this post, another approach is discussed. We solve this problem by treating this as a graph problem, where vertices will be the first and last character of strings, and we will draw an edge between two vertices if they are the first and last character of the same string, so a number of edges in the graph will be same as the number of strings in the array.
Graph representation of some string arrays are given in the below diagram,
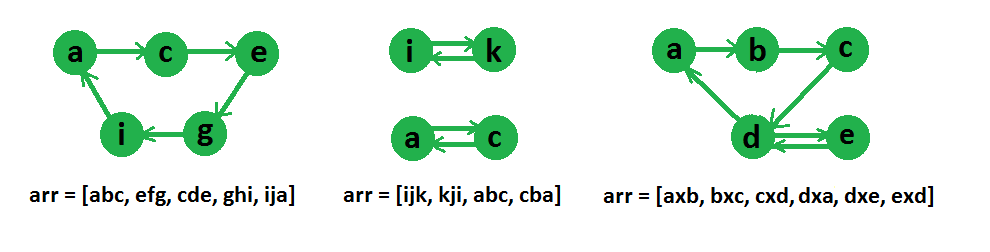
Now it can be clearly seen after graph representation that if a loop among graph vertices is possible then we can reorder the strings otherwise not. As in the above diagram’s example, a loop can be found in the first and third array of string but not in the second array of string. Now to check whether this graph can have a loop which goes through all the vertices, we’ll check two conditions,
- Indegree and Outdegree of each vertex should be the same.
- The graph should be strongly connected.
The first condition can be checked easily by keeping two arrays, in and out for each character. For checking whether a graph is having a loop which goes through all vertices is the same as checking complete directed graph is strongly connected or not because if it has a loop which goes through all vertices then we can reach to any vertex from any other vertex that is, the graph will be strongly connected and the same argument can be given for reverse statement also.
Now for checking the second condition we will just run a DFS from any character and visit all reachable vertices from this, now if the graph has a loop then after this one DFS all vertices should be visited, if all vertices are visited then we will return true otherwise false so visiting all vertices in a single DFS flags a possible ordering among strings.
C++
#include <bits/stdc++.h>
using namespace std;
#define M 26
void dfs(vector<int> g[], int u, vector<bool> &visit)
{
visit[u] = true;
for (int i = 0; i < g[u].size(); ++i)
if(!visit[g[u][i]])
dfs(g, g[u][i], visit);
}
bool isConnected(vector<int> g[], vector<bool> &mark, int s)
{
vector<bool> visit(M, false);
dfs(g, s, visit);
for (int i = 0; i < M; i++)
{
if (mark[i] && !visit[i])
return false;
}
return true;
}
bool possibleOrderAmongString(string arr[], int N)
{
vector<int> g[M];
vector<bool> mark(M, false);
vector<int> in(M, 0), out(M, 0);
for (int i = 0; i < N; i++)
{
int f = arr[i].front() - 'a';
int l = arr[i].back() - 'a';
mark[f] = mark[l] = true;
in[l]++;
out[f]++;
g[f].push_back(l);
}
for (int i = 0; i < M; i++)
if (in[i] != out[i])
return false;
return isConnected(g, mark, arr[0].front() - 'a');
}
int main()
{
string arr[] = {"ab", "bc", "cd", "de", "ed", "da"};
int N = sizeof(arr) / sizeof(arr[0]);
if (possibleOrderAmongString(arr, N) == false)
cout << "Ordering not possible\n";
else
cout << "Ordering is possible\n";
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
public static boolean possibleOrderAmongString(
String s[], int n)
{
int m = 26;
boolean mark[] = new boolean[m];
int in[] = new int[26];
int out[] = new int[26];
ArrayList<
ArrayList<Integer>> adj = new ArrayList<
ArrayList<Integer>>();
for(int i = 0; i < m; i++)
adj.add(new ArrayList<>());
for(int i = 0; i < n; i++)
{
int f = (int)(s[i].charAt(0) - 'a');
int l = (int)(s[i].charAt(
s[i].length() - 1) - 'a');
mark[f] = mark[l] = true;
in[l]++;
out[f]++;
adj.get(f).add(l);
}
for(int i = 0; i < m; i++)
{
if (in[i] != out[i])
return false;
}
return isConnected(adj, mark,
s[0].charAt(0) - 'a');
}
public static boolean isConnected(
ArrayList<ArrayList<Integer>> adj,
boolean mark[], int src)
{
boolean visited[] = new boolean[26];
dfs(adj, visited, src);
for(int i = 0; i < 26; i++)
{
if (mark[i] && !visited[i])
return false;
}
return true;
}
public static void dfs(ArrayList<ArrayList<Integer>> adj,
boolean visited[], int src)
{
visited[src] = true;
for(int i = 0; i < adj.get(src).size(); i++)
if (!visited[adj.get(src).get(i)])
dfs(adj, visited, adj.get(src).get(i));
}
public static void main(String[] args)
{
String s[] = { "ab", "bc", "cd", "de", "ed", "da" };
int n = s.length;
if (possibleOrderAmongString(s, n))
System.out.println("Ordering is possible");
else
System.out.println("Ordering is not possible");
}
}
|
Python3
M = 26
def dfs(g, u, visit):
visit[u] = True
for i in range(len(g[u])):
if(not visit[g[u][i]]):
dfs(g, g[u][i], visit)
def isConnected(g, mark, s):
visit = [False for i in range(M)]
dfs(g, s, visit)
for i in range(M):
if(mark[i] and (not visit[i])):
return False
return True
def possibleOrderAmongString(arr, N):
g = {}
mark = [False for i in range(M)]
In = [0 for i in range(M)]
out = [0 for i in range(M)]
for i in range(N):
f = (ord(arr[i][0]) -
ord('a'))
l = (ord(arr[i][-1]) -
ord('a'))
mark[f] = True
mark[l] = True
In[l] += 1
out[f] += 1
if f not in g:
g[f] = []
g[f].append(l)
for i in range(M):
if(In[i] != out[i]):
return False
return isConnected(g, mark,
ord(arr[0][0]) -
ord('a'))
arr = ["ab", "bc",
"cd", "de",
"ed", "da"]
N = len(arr)
if(possibleOrderAmongString(arr, N) ==
False):
print("Ordering not possible")
else:
print("Ordering is possible")
|
C#
using System;
using System.Collections.Generic;
class GFG {
static bool possibleOrderAmongString(string[] s, int n)
{
int m = 26;
bool[] mark = new bool[m];
int[] In = new int[26];
int[] Out = new int[26];
List<List<int>> adj = new List<List<int>>();
for(int i = 0; i < m; i++)
adj.Add(new List<int>());
for(int i = 0; i < n; i++)
{
int f = (int)(s[i][0] - 'a');
int l = (int)(s[i][s[i].Length - 1] - 'a');
mark[f] = mark[l] = true;
In[l]++;
Out[f]++;
adj[f].Add(l);
}
for(int i = 0; i < m; i++)
{
if (In[i] != Out[i])
return false;
}
return isConnected(adj, mark,
s[0][0] - 'a');
}
public static bool isConnected(
List<List<int>> adj,
bool[] mark, int src)
{
bool[] visited = new bool[26];
dfs(adj, visited, src);
for(int i = 0; i < 26; i++)
{
if (mark[i] && !visited[i])
return false;
}
return true;
}
public static void dfs(List<List<int>> adj,
bool[] visited, int src)
{
visited[src] = true;
for(int i = 0; i < adj[src].Count; i++)
if (!visited[adj[src][i]])
dfs(adj, visited, adj[src][i]);
}
static void Main() {
string[] s = { "ab", "bc", "cd", "de", "ed", "da" };
int n = s.Length;
if (possibleOrderAmongString(s, n))
Console.Write("Ordering is possible");
else
Console.Write("Ordering is not possible");
}
}
|
Javascript
<script>
function possibleOrderAmongString(s, n)
{
let m = 26;
let mark = new Array(m);
mark.fill(false);
let In = new Array(26);
In.fill(0);
let Out = new Array(26);
Out.fill(0);
let adj = [];
for(let i = 0; i < m; i++)
adj.push([]);
for(let i = 0; i < n; i++)
{
let f = (s[i][0].charCodeAt() - 'a'.charCodeAt());
let l = (s[i][s[i].length - 1].charCodeAt() - 'a'.charCodeAt());
mark[f] = mark[l] = true;
In[l]++;
Out[f]++;
adj[f].push(l);
}
for(let i = 0; i < m; i++)
{
if (In[i] != Out[i])
return false;
}
return isConnected(adj, mark, s[0][0].charCodeAt() - 'a'.charCodeAt());
}
function isConnected(adj, mark, src)
{
let visited = new Array(26);
visited.fill(false);
dfs(adj, visited, src);
for(let i = 0; i < 26; i++)
{
if (mark[i] && !visited[i])
return false;
}
return true;
}
function dfs(adj, visited, src)
{
visited[src] = true;
for(let i = 0; i < adj[src].length; i++)
if (!visited[adj[src][i]])
dfs(adj, visited, adj[src][i]);
}
let s = [ "ab", "bc", "cd", "de", "ed", "da" ];
let n = s.length;
if (possibleOrderAmongString(s, n))
document.write("Ordering is possible");
else
document.write("Ordering is not possible");
</script>
|
Output
Ordering is possible
Time complexity: O(n)
Auxiliary Space: O(n)
Share your thoughts in the comments
Please Login to comment...