Implementation of Perceptron Algorithm for NOT Logic Gate

In the field of Machine Learning, the Perceptron is a Supervised Learning Algorithm for binary classifiers. The Perceptron Model implements the following function:

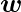
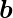
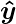
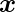
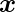
For a particular choice of the weight vector and bias parameter , the model predicts output for the corresponding input vector . NOT logical function truth table is of only 1-bit binary input (0 or 1), i.e, the input vector and the corresponding output –

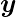
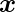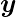0	1
1	0

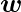
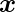
Now for the corresponding weight vector of the input vector , the associated Perceptron Function can be defined as:

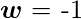
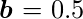
For the implementation, considered weight parameter is and the bias parameter is . Python Implementation:

# importing Python library
import numpy as np

# define Unit Step Function
def unitStep(v):
    if v >= 0:
        return 1
    else:
        return 0

# design Perceptron Model
def perceptronModel(x, w, b):
    v = np.dot(w, x) + b
    y = unitStep(v)
    return y

# NOT Logic Function
# w = -1, b = 0.5
def NOT_logicFunction(x):
    w = -1
    b = 0.5
    return perceptronModel(x, w, b)

# testing the Perceptron Model
test1 = np.array(1)
test2 = np.array(0)

print("NOT({}) = {}".format(1, NOT_logicFunction(test1)))
print("NOT({}) = {}".format(0, NOT_logicFunction(test2)))

Output:

NOT(1) = 0
NOT(0) = 1

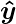
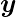
Here, the model predicted output () for each of the test inputs are exactly matched with the NOT logic gate conventional output () according to the truth table. Hence, it is verified that the perceptron algorithm for NOT logic gate is correctly implemented.