Implementation of BFS using adjacency matrix
Last Updated :
15 Feb, 2023
Breadth First Search (BFS) has been discussed in this article which uses adjacency list for the graph representation. In this article, adjacency matrix will be used to represent the graph.
Adjacency matrix representation: In adjacency matrix representation of a graph, the matrix mat[][] of size n*n (where n is the number of vertices) will represent the edges of the graph where mat[i][j] = 1 represents that there is an edge between the vertices i and j while mat[i][j] = 0 represents that there is no edge between the vertices i and j.
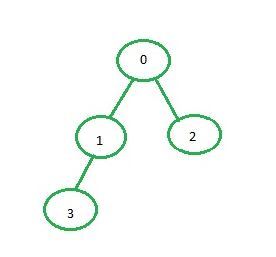
Below is the adjacency matrix representation of the graph shown in the above image:
0 1 2 3
0 0 1 1 0
1 1 0 0 1
2 1 0 0 0
3 0 1 0 0
Examples:
Input: source = 0

Output: 0 1 2 3
Input: source = 1
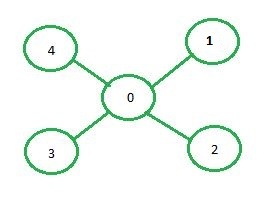
Output:1 0 2 3 4
Approach:
- Create a matrix of size n*n where every element is 0 representing there is no edge in the graph.
- Now, for every edge of the graph between the vertices i and j set mat[i][j] = 1.
- After the adjacency matrix has been created and filled, find the BFS traversal of the graph as described in this post.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> adj;
void addEdge(int x,int y)
{
adj[x][y] = 1;
adj[y][x] = 1;
}
void bfs(int start)
{
vector<bool> visited(adj.size(), false);
vector<int> q;
q.push_back(start);
visited[start] = true;
int vis;
while (!q.empty()) {
vis = q[0];
cout << vis << " ";
q.erase(q.begin());
for (int i = 0; i < adj[vis].size(); i++) {
if (adj[vis][i] == 1 && (!visited[i])) {
q.push_back(i);
visited[i] = true;
}
}
}
}
int main()
{
int v = 5;
adj= vector<vector<int>>(v,vector<int>(v,0));
addEdge(0,1);
addEdge(0,2);
addEdge(1,3);
bfs(0);
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
class GFG{
static class Graph
{
int v;
int e;
int[][] adj;
Graph(int v, int e)
{
this.v = v;
this.e = e;
adj = new int[v][v];
for(int row = 0; row < v; row++)
Arrays.fill(adj[row], 0);
}
void addEdge(int start, int e)
{
adj[start][e] = 1;
adj[e][start] = 1;
}
void BFS(int start)
{
boolean[] visited = new boolean[v];
Arrays.fill(visited, false);
List<Integer> q = new ArrayList<>();
q.add(start);
visited[start] = true;
int vis;
while (!q.isEmpty())
{
vis = q.get(0);
System.out.print(vis + " ");
q.remove(q.get(0));
for(int i = 0; i < v; i++)
{
if (adj[vis][i] == 1 && (!visited[i]))
{
q.add(i);
visited[i] = true;
}
}
}
}
}
public static void main(String[] args)
{
int v = 5, e = 4;
Graph G = new Graph(v, e);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(1, 3);
G.BFS(0);
}
}
|
Python3
class Graph:
adj = []
def __init__(self, v, e):
self.v = v
self.e = e
Graph.adj = [[0 for i in range(v)]
for j in range(v)]
def addEdge(self, start, e):
Graph.adj[start][e] = 1
Graph.adj[e][start] = 1
def BFS(self, start):
visited = [False] * self.v
q = [start]
visited[start] = True
while q:
vis = q[0]
print(vis, end = ' ')
q.pop(0)
for i in range(self.v):
if (Graph.adj[vis][i] == 1 and
(not visited[i])):
q.append(i)
visited[i] = True
v, e = 5, 4
G = Graph(v, e)
G.addEdge(0, 1)
G.addEdge(0, 2)
G.addEdge(1, 3)
G.BFS(0)
|
C#
using System;
using System.Collections.Generic;
public class GFG{
class Graph
{
public int v;
public int e;
public int[,] adj;
public Graph(int v, int e)
{
this.v = v;
this.e = e;
adj = new int[v,v];
for(int row = 0; row < v; row++)
for(int col = 0; col < v; col++)
adj[row, col] = 0;
}
public void addEdge(int start, int e)
{
adj[start, e] = 1;
adj[e, start] = 1;
}
public void BFS(int start)
{
bool[] visited = new bool[v];
List<int> q = new List<int>();
q.Add(start);
visited[start] = true;
int vis;
while (q.Count != 0)
{
vis = q[0];
Console.Write(vis + " ");
q.Remove(q[0]);
for(int i = 0; i < v; i++)
{
if (adj[vis,i] == 1 && (!visited[i]))
{
q.Add(i);
visited[i] = true;
}
}
}
}
}
public static void Main(String[] args)
{
int v = 5, e = 4;
Graph G = new Graph(v, e);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(1, 3);
G.BFS(0);
}
}
|
Javascript
const adj = [];
function addEdge(x, y) {
adj[x][y] = 1;
adj[y][x] = 1;
}
function bfs(start) {
const visited = Array(adj.length).fill(false);
const q = [];
q.push(start);
visited[start] = true;
let vis;
while (q.length >0) {
vis = q.shift();
console.log(vis + " ");
for (let i = 0; i < adj[vis].length; i++) {
if (adj[vis][i] === 1 && !visited[i]) {
q.push(i);
visited[i] = true;
}
}
}
}
const v = 5;
for (let i = 0; i < v; i++) {
adj[i] = Array(v).fill(0);
}
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 3);
bfs(0);
|
Time Complexity: O(N*N)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...