How to discretize an Ellipse or Circle to a Polygon using C++ Graphics?
Last Updated :
17 Jan, 2020
In this article, we’ll see how to discretize an Ellipse (or a circle) into a polygon. Since a circle is just a specific case of an ellipse we’ll not discuss separately how to discretize a circle to a polygon!
Why discretize an ellipse to a polygon?
Discretization has several applications, the two most important being:
- Rendering Curves: Curves cannot be rendered directly on the screen. They first need to be approximated to polygons (in case of Circles and ellipses) or chained-line-segments (in case of Bezier curves and splines) and discretization serves that purpose! *
- Collision-Detection: While checking intersection for curves like Circle and Bezier curve is simple, some curves like Ellipses are way too complicated and checking intersection for them precisely is very inefficient! Hence they are first discretized to simple shapes like rectangle, polygon, etc for which collision can be detected efficiently!
* While one can render curves pixel by pixel with Bresengham’s algorithm, it is often not the best practice! Since modern GPUs have become much more powerful they can render a series of the pixel without any bloat! Also drawing any curve pixel by pixel strips any possibility of batching and GPU “memorization”! And because of the way modern CPUs work trigonometric functions are no longer “computationally expensive” (atleast most of the time)!
Proof-of-concept: So the main idea of discretizing an ellipse is to break the ellipse into vertices representing polygon whereby the number of segments of the polygon would either be calculated automatically or given by the client user! For this example, we’ll not calculate the number of segments automatically!
We’ll use C Borland Graphics API but the same principles can be applied to any graphics library! Linux Users may want to use
SDL libgraph as a replacement for Borland Graphics Library! Also we’ll use C++ instead of C to use the built-in
pair data-structure that STL provides (and also for function-overloading that will come handy later)!
Rendering Polygons:
As it turns out, the Borland Graphics API doesn’t actually have a multi-format polygon rendering function like modern graphics libraries have! There’s
drawPoly and
fillPoly but the representation of the polygon might not make sense to some people and also it might lead us to some pointer problems. So we’ll implement our own polygon rendering function! We’ll represent a polygon as a vector of pairs of integers representing the vertices of the polygon! The main benefit of this is that a vector always knows it’s size, unlike arrays which under the hood is just a pointer unknown of its bounds.
In any case, here’s our code for rendering a polygon in Borland Graphics Library:-
#include <algorithm>
#include <graphics.h>
using namespace std;
typedef pair<int, int> vertex;
void polygon(vector<vertex>& vertices)
{
for (int i = 0, n = vertices.size(); i < n; i++) {
vertex current = vertices[i], next;
next = vertices[(i == n - 1) ? 0 : i + 1];
int x1 = current.first, y1 = current.second;
int x2 = next.first, y2 = next.second;
line(x1, y1, x2, y2);
}
}
int main()
{
int gd = DETECT, gm;
initgraph(&gd, &gm, "");
vector<vertex> vertices;
vertices.push_back(vertex(340, 150));
vertices.push_back(vertex(220, 250));
vertices.push_back(vertex(340, 350));
polygon(vertices);
delay(5000);
}
|
Output:

Discretizing Ellipse to Polygon:
Now that we can render polygons we are ready to discretize an ellipse to a polygon!
So the key to discretizing an ellipse is to have a moving point that moves across the ellipse in equal intervals and creating a vertex on every such point (every point where the moving point passes over)! For this one must know the parametric form of an ellipse which is:-
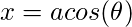

Based on the above formula, here’s the code-snippet that discretizes our ellipse to a polygon:-
#define TWO_PI 44 / 7.0f
vector<vertex> discretizeEllipse(
int x, int y,
int a, int b,
int seg)
{
float angle_shift = TWO_PI / seg, phi = 0;
vector<vertex> vertices;
for (int i = 0; i < seg; ++i) {
phi += angle_shift;
vertices
.push_back(
vertex(
x + a * cos(phi),
y + b * sin(phi)));
}
return vertices;
}
|
One last thing that’s left to do is
overload the function such that the last parameter is not needed! We can set
segments to some default value but we’d like it to be calculated based on the dimensions of the ellipse! So here’s the second overload:-
vector<vertex> discretizeEllipse(
int x, int y,
int a, int b)
{
int segments
= max((int)floor(
sqrt(((a + b) / 2) * 20)),
8);
return discretizeEllipse(
x, y,
a, b,
segments);
}
|
To end this article, here’s the complete source-code:
#include <algorithm>
#include <graphics.h>
#define TWO_PI 44 / 7.0f
typedef pair<int, int> vertex;
void polygon(vector<vertex> vertices)
{
for (int i = 0, n = vertices.size(); i < n; i++) {
vertex current = vertices[i], next;
next = vertices[(i == n - 1) ? 0 : i + 1];
int x1 = current.first, y1 = current.second;
int x2 = next.first, y2 = next.second;
line(x1, y1, x2, y2);
}
}
vector<vertex> discretizeEllipse(
int x, int y, int a,
int b, int seg)
{
float angle_shift = TWO_PI / seg, phi = 0;
vector<vertex> vertices;
for (int i = 0; i < seg; ++i) {
phi += angle_shift;
vertices.push_back(
vertex(
x + a * cos(phi),
y + b * sin(phi)));
}
return vertices;
}
vector<vertex> discretizeEllipse(
int x, int y, int a, int b)
{
int segments
= max((int)floor(
sqrt(((a + b) / 2) * 20)),
8);
return discretizeEllipse(
x, y, a, b, segments);
}
int main()
{
int gd = DETECT, gm;
initgraph(&gd, &gm, "");
polygon(discretizeEllipse(320, 240, 200, 100));
polygon(discretizeEllipse(320, 240, 200, 100, 8));
delay(5000);
}
|
Output:

Share your thoughts in the comments
Please Login to comment...