How is the time complexity of Sieve of Eratosthenes is n*log(log(n))?
Last Updated :
24 Jan, 2023
Pre-requisite: Sieve of Eratosthenes What is Sieve of Eratosthenes algorithm? In order to analyze it, let's take a number n and the task is to print the prime numbers less than n. Therefore, by definition of Sieve of Eratosthenes, for every prime number, it has to check the multiples of the prime and mark it as composite. This process continues until a value p which is the highest prime number less than n. Understanding the n*log(log n) time complexity of Sieve of Eratosthenes
- If it is assumed that the time taken to mark a number as composite is constant, then the number of times the loop runs is equal to:
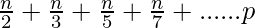
- On taking n common from the above equation, the above equation can be rewritten as:
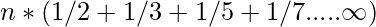
- It can be proved as below with the help of Harmonic Progression of the sum of primes:
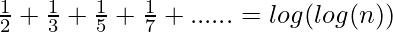
- Proof of Harmonic Progression of the sum of primes: In order to understand the proof, the prerequisite is the Harmonic series and Taylor series expansion.
- Lets take an the equation:
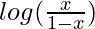
- The taylor series expansion of the above equation is given by:
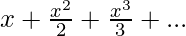
- Putting x = 1 in the above equation, we get the relation:
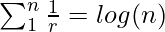 Let’s mark the above equation as 1.
Let’s mark the above equation as 1. - From Euler’s product formula,
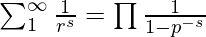
-
- On substituting s = 1 in the above equation, we get
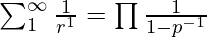
- On applying log to both the sides:
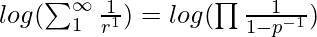
- On simplifying the above equation, it becomes:
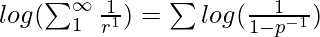
- In the above equation, 1 > p-1 > -1
- Thus, we can use taylor series expansion for the right hand side of the above equation.

- On substituting this in the above equation, we get:
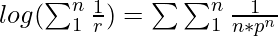 where p is a prime number.
where p is a prime number. - On expanding the inner summation;
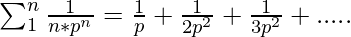
- The above series is convergent. So, the above series can be approximated to:
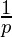
- Therefore, on substituting and rewriting the equation; we get
 where p is the prime number.
where p is the prime number. - From the initial equation 1, we can finally conclude that:
 where p is the sum of prime numbers.
where p is the sum of prime numbers.
- On substituting this in the equation, we get the time complexity as:

Hence the time complexity of Sieve of Eratosthenes is n*log(log(n)) Reference: Divergence of the sum of the reciprocals of the primes
Share your thoughts in the comments
Please Login to comment...