What does Big O – O(log N) complexity mean?

In the field of computer science and algorithm analysis, Big O notation is a tool used to describe how algorithms perform. It provides a way to estimate how the runtime of an algorithm changes, as the input data size increases. One interesting and efficient complexity in Big O notation is O(log N). In this article, we will look at the concept of O(log(N)) complexity and how it can be achieved.

What does Big O Notation mean?

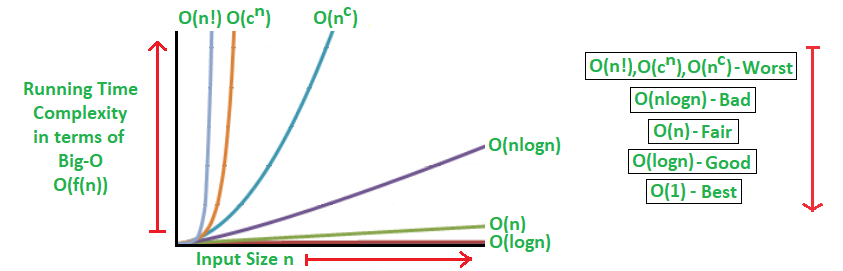
Big O notation is a representation used to indicate the bound of an algorithm’s time complexity relative to its input size. It enables us to make approximations about how an algorithm performance will behave as the input size grows significantly. The “O” in Big O stands for “order ” while the value within parentheses indicates the growth rate of the algorithm.

In the case of O(N), we refer to it as complexity. This implies that the execution time of the algorithm increases proportionally with respect, to the size of the input. If we double our input size we can expect twice as much execution time. Linear complexity is one of the encountered complexities when working with algorithms.

Big O Notation

What does O(log N) Complexity?

The notation O(log N) represents logarithmic time complexity in algorithm analysis. Specifically, it indicates that the time complexity of an algorithm grows logarithmically with the size of the input (N).

In a logarithmic time complexity, as the input size increases, the time required to perform the algorithm’s operations increases at a rate proportional to the logarithm of the input size. This is considered very efficient compared to linear (O(N)), quadratic (O(N^2)), or cubic (O(N^3)) time complexities, especially for large input sizes.

One of the known examples of an algorithm with O(log N) complexity is the Binary Search Algorithm. It efficiently locates an element in an array by following these steps:

1. Start with the element of the array.
2. If the target element matches the element then you have found it.
3. If the target element is smaller than the element narrow down your search to the half of the array.
4. If the target element is greater than the element narrow down your search to the half of the array.
5. Repeat steps 1-4 until you find your desired target element.

The key idea behind search is that it reduces its search space by half with each iteration. This characteristic gives it a logarithmic time complexity of O(log N) where ‘N’ represents how many elements are present, in an array.

Below is the implementation of searching an element in an array using Binary Search:

C++

#include <bits/stdc++.h>
using namespace std;

int binary_search(const vector<int>& arr, int target)
{
    int left = 0;
    int right = arr.size() - 1;

    while (left <= right) {

        // Calculate the midpoint to prevent integer
        // overflow
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) {

            // Found the target element
            return mid;
        }
        else if (arr[mid] < target) {

            // Adjust the search range to the right half
            left = mid + 1;
        }
        else {

            // Adjust the search range to the left half
            right = mid - 1;
        }
    }

    return -1; // Element not found
}

// Driver code.
int main()
{
    vector<int> sorted_array
        = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
    int target_element = 5;

    int result
        = binary_search(sorted_array, target_element);

    if (result != -1) {
        cout << "Element " << target_element
             << " found at index " << result << "." << endl;
    }
    else {
        cout << "Element " << target_element
             << " not found." << endl;
    }

    return 0;
}

Java

import java.util.Arrays;

public class BinarySearch {

    static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;

        while (left <= right) {
            // Calculate the midpoint to prevent integer overflow
            int mid = left + (right - left) / 2;

            if (arr[mid] == target) {
                // Found the target element
                return mid;
            } else if (arr[mid] < target) {
                // Adjust the search range to the right half
                left = mid + 1;
            } else {
                // Adjust the search range to the left half
                right = mid - 1;
            }
        }

        return -1; // Element not found
    }

    public static void main(String[] args) {
        int[] sortedArray = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
        int targetElement = 5;

        int result = binarySearch(sortedArray, targetElement);

        if (result != -1) {
            System.out.println("Element " + targetElement + " found at index " + result + ".");
        } else {
            System.out.println("Element " + targetElement + " not found.");
        }
    }
}

// This code is contributed by shivamgupta310570

Python3

def binary_search(arr, target):
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = left + (right - left) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    return -1

# Driver code
if __name__ == "__main__":
    sorted_array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    target_element = 5

    result = binary_search(sorted_array, target_element)

    if result != -1:
        print(f"Element {target_element} found at index {result}.")
    else:
        print(f"Element {target_element} not found.")

C#

using System;
using System.Collections.Generic;

class Program
{
    static int BinarySearch(List<int> arr, int target)
    {
        int left = 0;
        int right = arr.Count - 1;

        while (left <= right)
        {
            // Calculate the midpoint to prevent integer overflow
            int mid = left + (right - left) / 2;
            if (arr[mid] == target)
            {
                // Found the target element
                return mid;
            }
            else if (arr[mid] < target)
            {
                // Adjust the search range to the right half
                left = mid + 1;
            }
            else
            {
                // Adjust the search range to the left half
                right = mid - 1;
            }
        }

        return -1; // Element not found
    }

    static void Main()
    {
        List<int> sortedArray = new List<int> { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
        int targetElement = 5;

        int result = BinarySearch(sortedArray, targetElement);

        if (result != -1)
        {
            Console.WriteLine($"Element {targetElement} found at index {result}.");
        }
        else
        {
            Console.WriteLine($"Element {targetElement} not found.");
        }
    }
}

Javascript

function binarySearch(arr, target) {
    let left = 0;
    let right = arr.length - 1;

    while (left <= right) {
        // Calculate the midpoint to prevent integer overflow
        let mid = Math.floor(left + (right - left) / 2);

        if (arr[mid] === target) {
            // Found the target element
            return mid;
        } else if (arr[mid] < target) {
            // Adjust the search range to the right half
            left = mid + 1;
        } else {
            // Adjust the search range to the left half
            right = mid - 1;
        }
    }

    return -1; // Element not found
}

// Driver code
const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 9];
const targetElement = 5;

const result = binarySearch(sortedArray, targetElement);

if (result !== -1) {
    console.log(`Element ${targetElement} found at index ${result}.`);
} else {
    console.log(`Element ${targetElement} not found.`);
}

Output

Element 5 found at index 4.

Time Complexity: O(log(N))
Auxiliary Space: O(1)

Importance of O(log N) Complexity:

• Efficiency: Algorithms with an O(log N) time complexity are super efficient especially when it comes to tasks like searching and sorting.
• Scalability: O(log N) algorithms can handle amounts of data without causing an increase in runtime. This is particularly important for applications like databases and network routing.
• Divide and Conquer: Algorithms with O(log N) complexity follow a “divide and conquer” strategy to solve problems by breaking them down into smaller solvable subproblems

Conclusion

In summary understanding O(log N) complexity is really important because it combines efficiency, scalability and elegance in algorithm design. Algorithms that exhibit behavior (like search) play a crucial role in computer science and software development. Having a grasp of this concept helps developers make decisions when choosing algorithms ultimately optimizing their applications performance. Whether you’re new to coding or an experienced engineer having an understanding of O(log N) complexity is invaluable, for your toolkit.