Heighway’s Dragon Curve using Python
Last Updated :
29 Sep, 2022
Introduction | Dragon Curve
A Dragon curve is a recursive non-intersecting curve also known as the Harter–Heighway dragon or the Jurassic Park dragon curve. It is a mathematical curve which can be approximated by recursive methods such as Lindenmayer systems. Lindenmayer systems: A Lindenmayer system, also known as an L-system, is a string rewriting system that can be used to generate fractals. Two principal areas include generation of fractals and realistic modeling of plants. Lindenmayer system begins with a string of symbols called the axiom and applies to the axiom a set of production rules which are used to rewrite the axiom. Recursive L-System are more interesting as it replaces a symbol with a copy of itself plus something extra.L-system follow some rules:
An L-system is a formal grammar consisting of 4 parts:
1. A set of variables: symbols that can be replaced by production rules.
2. A set of constants: symbols that do not get replaced.e.g: !, [, ], +, -.
3. A single axiom: a string & is the initial state of the system.
4. A set of production rules: defining the way/rule variables can be replaced.
Let’s take the example of the following L-system: L-System Rules
| Recursion L-System |
|
| axiom |
skk |
| rules |
s = ksk |
| generation 1: |
(ksk)kk = kskkk |
| generation 2: |
k(ksk)kkk = kkskkkk |
| generation 3: |
kk(ksk)kkkk = kkkskkkkk |
gen 1 takes help of gen 0 (axiom)
generation 1 -> apply rule in generation 0
generation 0 = skk
replace s with "ksk" in gen 0 to get gen 1
gen 1 = (s)kk = (ksk)kk = kskskk
replace s with "ksk" in gen 1 to get gen 2
Iterate the same rule for all generations
Recursive L-systems, often produce intricately complex patterns that are self-similar across multiple scales.These complex patterns can be visualized with the help of a graphical interpretation applied to L-Systems based on turtle graphics.When L-systems are used with turtle graphics, a state of the turtle is defined as a quadruple (x, y, a, c). The Cartesian coordinates (x, y) represent the turtle’s position. The angle a, called the heading is interpreted as the direction in which the turtle is facing. The color c is interpreted as the color pen that the turtle currently has pressed to the floor so that any movement of the turtle will create a line of that color. Given the step size d and the angle increment b, the turtle can respond to symbols in an L-system string according to the following instructions:
Move forward (in the dir of the current heading) a distance d while drawing a line of color c.
The state of the turtle changes to (x', y', a, c), where
x' = x + d cos(a) and y' = y + d sin(a)
Dragon Curve L-system
The finite approximation of Dragon curve can be created with an L-System.The Dragon curve L-system can be represented as :
| Dragon Curve L-System |
|
| variables: |
f h |
| constants: |
+ – |
| axiom: |
f |
| rules: |
f = f-h
h = f+h |
| angle increment: |
90 degrees |
| generation 1: |
f-h |
| generation 2: |
f-h – f+h |
| generation 3: |
f-h – f+h – f-h + f+h |
| generation 4: |
f-h – f+h – f-h + f+h – f-h – f+h + f-h + f+h |
2 rules
/ \
replace f with f-h replace h with f+h
+ & - are constants
build up generations by following rules on axiom
gen 1 forms gen 2; gen 2 forms gen 3 and so on...
The generation 2 string is: 'f-h - f+h'
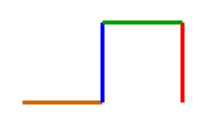 In the above L-system, assuming that the initial heading of the turtle is upward on the screen, then the first ‘f’ will draw a line straight up. The ‘-‘ causes the turtle to change its heading by 90 degrees to be pointed directly to the left. The ‘h’ draws a line directly to the left of the screen. The second ‘-‘ symbol again turns the turtle 90 degrees to its left which is directly down on the screen. The f symbol draws a unit length line in the down direction. The last turn symbol in the string is a ‘+’ which turns the turtle to its right by 90 degrees. However, since current heading of the turtle is pointed downward, its right is the screen’s left, so again the turtle’s heading is to the left of the screen. Finally, the h symbol draws a unit length line to the screen’s left.Hence we get the colorful resulting image. If we keep on forming more generations, we get beautiful curves called the dragon curves.As we can see below, the curve gets more intricate and complex as we grow in generations. Iteration 3:
In the above L-system, assuming that the initial heading of the turtle is upward on the screen, then the first ‘f’ will draw a line straight up. The ‘-‘ causes the turtle to change its heading by 90 degrees to be pointed directly to the left. The ‘h’ draws a line directly to the left of the screen. The second ‘-‘ symbol again turns the turtle 90 degrees to its left which is directly down on the screen. The f symbol draws a unit length line in the down direction. The last turn symbol in the string is a ‘+’ which turns the turtle to its right by 90 degrees. However, since current heading of the turtle is pointed downward, its right is the screen’s left, so again the turtle’s heading is to the left of the screen. Finally, the h symbol draws a unit length line to the screen’s left.Hence we get the colorful resulting image. If we keep on forming more generations, we get beautiful curves called the dragon curves.As we can see below, the curve gets more intricate and complex as we grow in generations. Iteration 3:  Iteration 9:
Iteration 9: 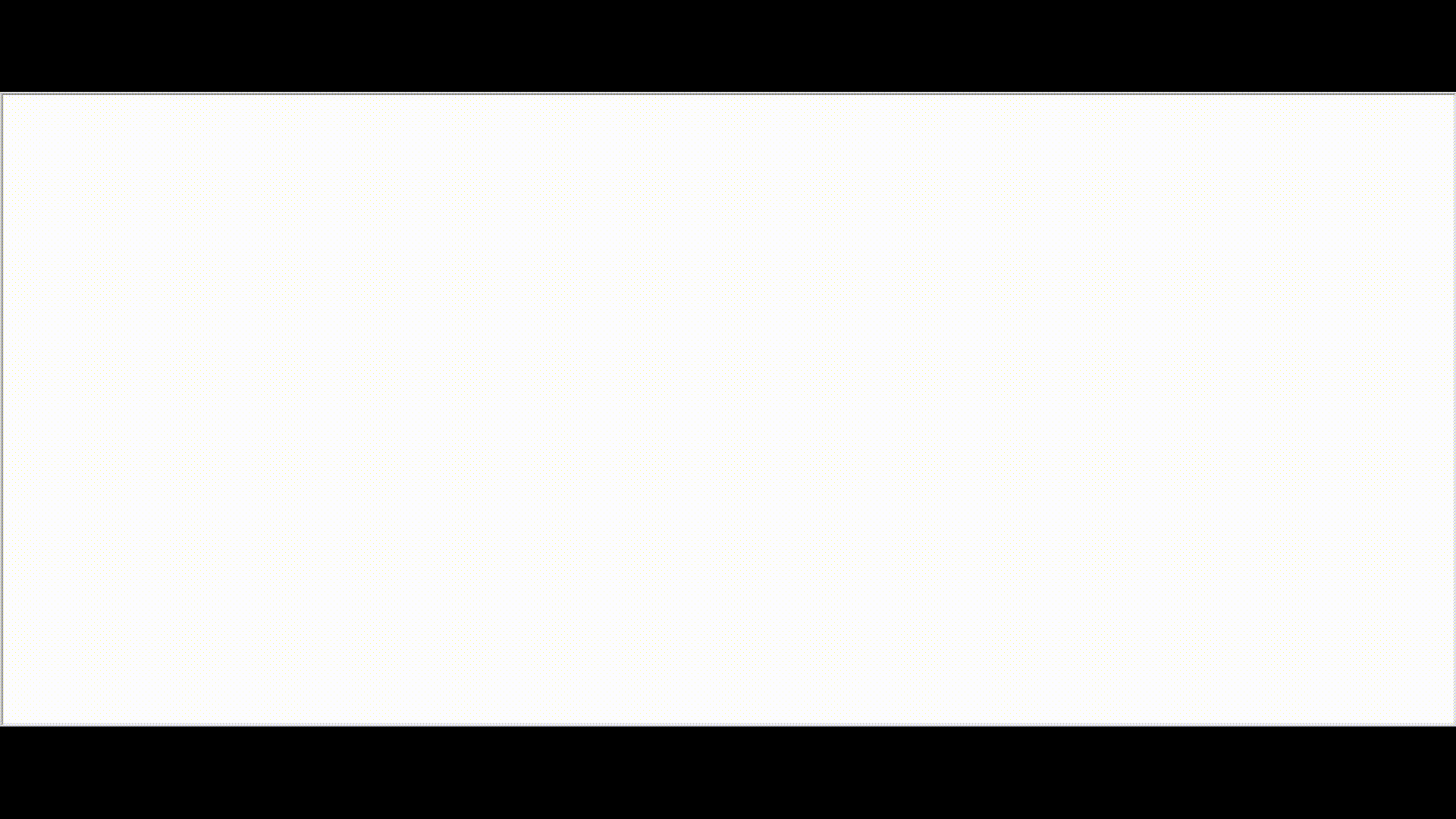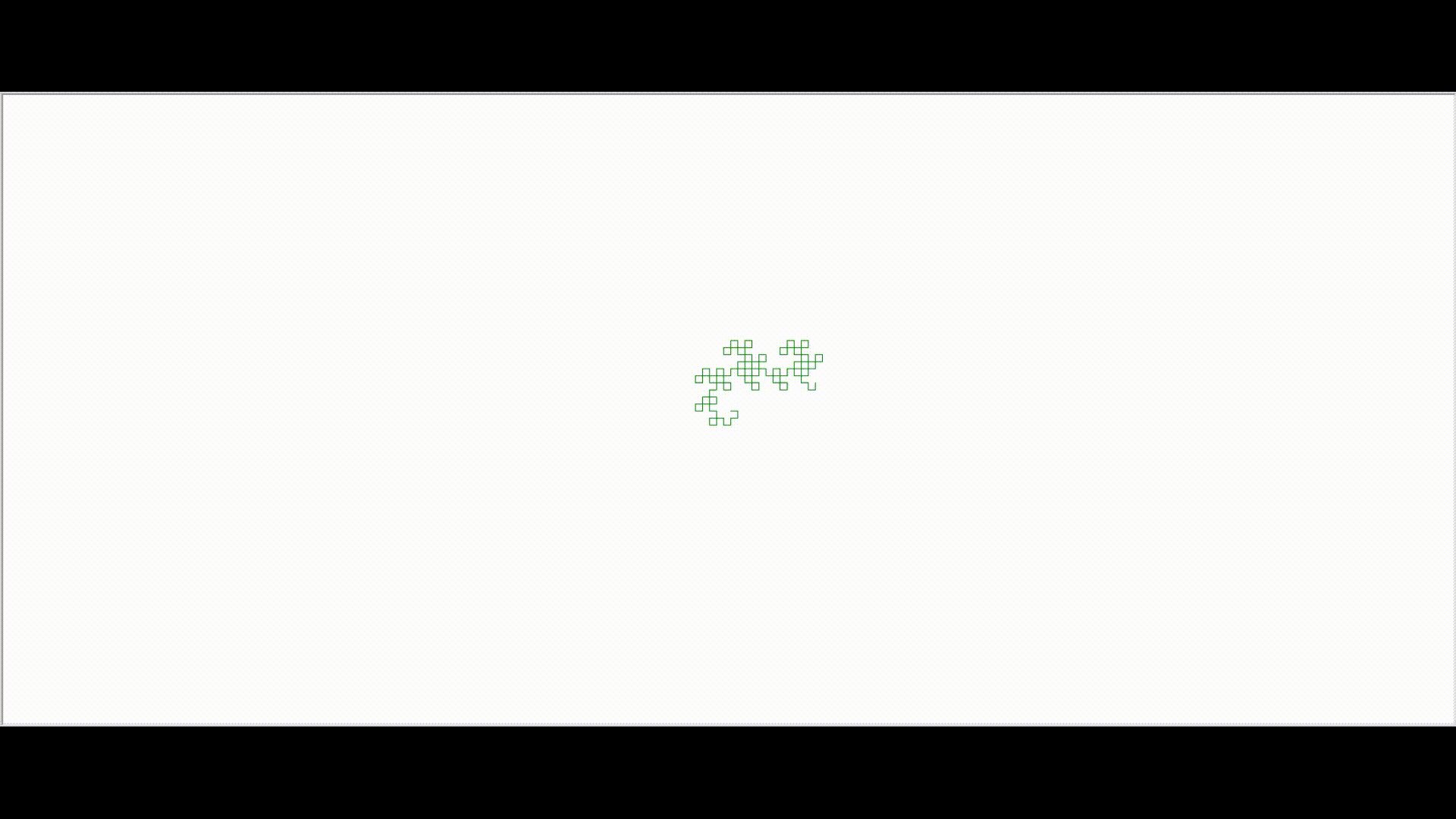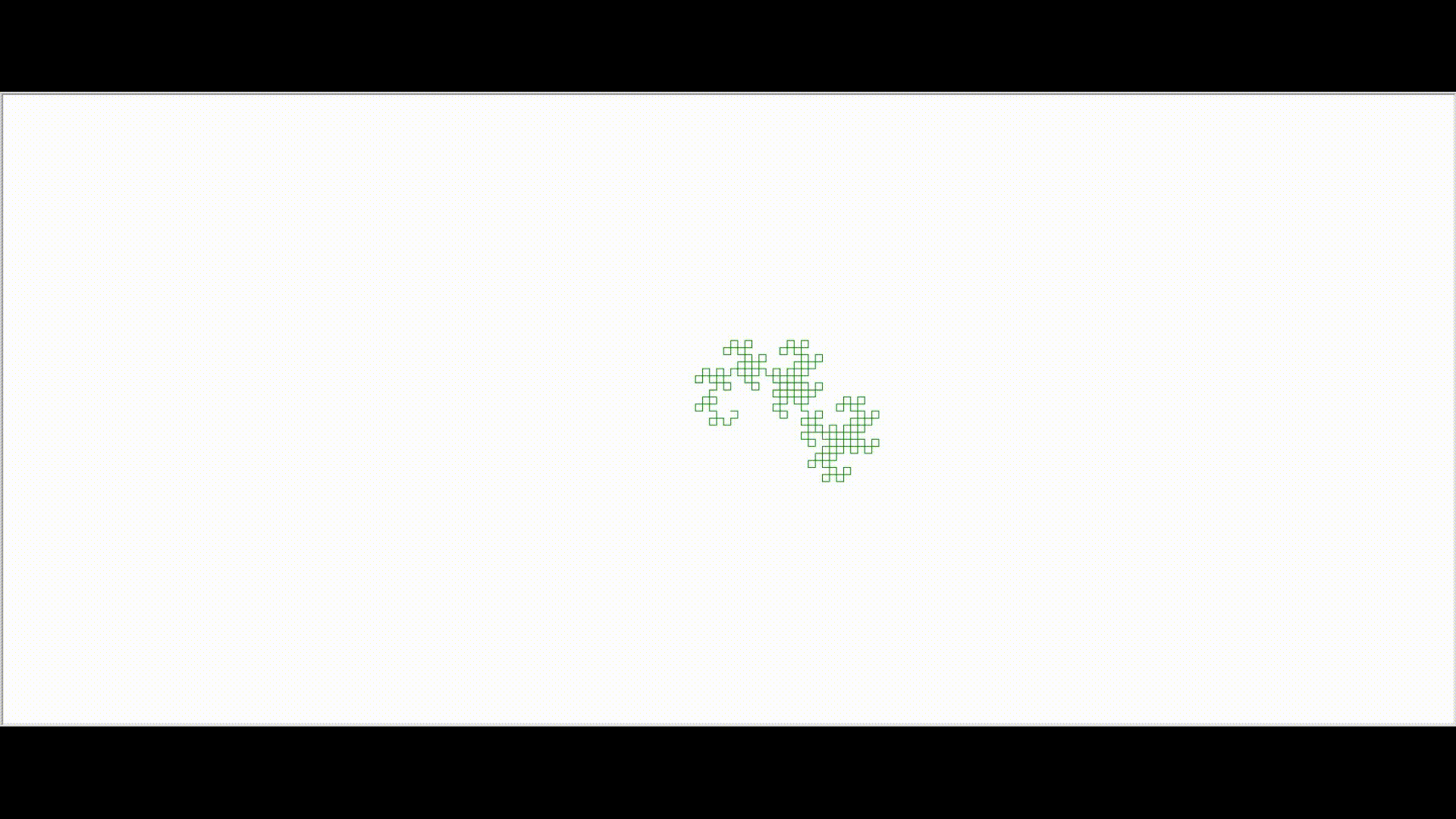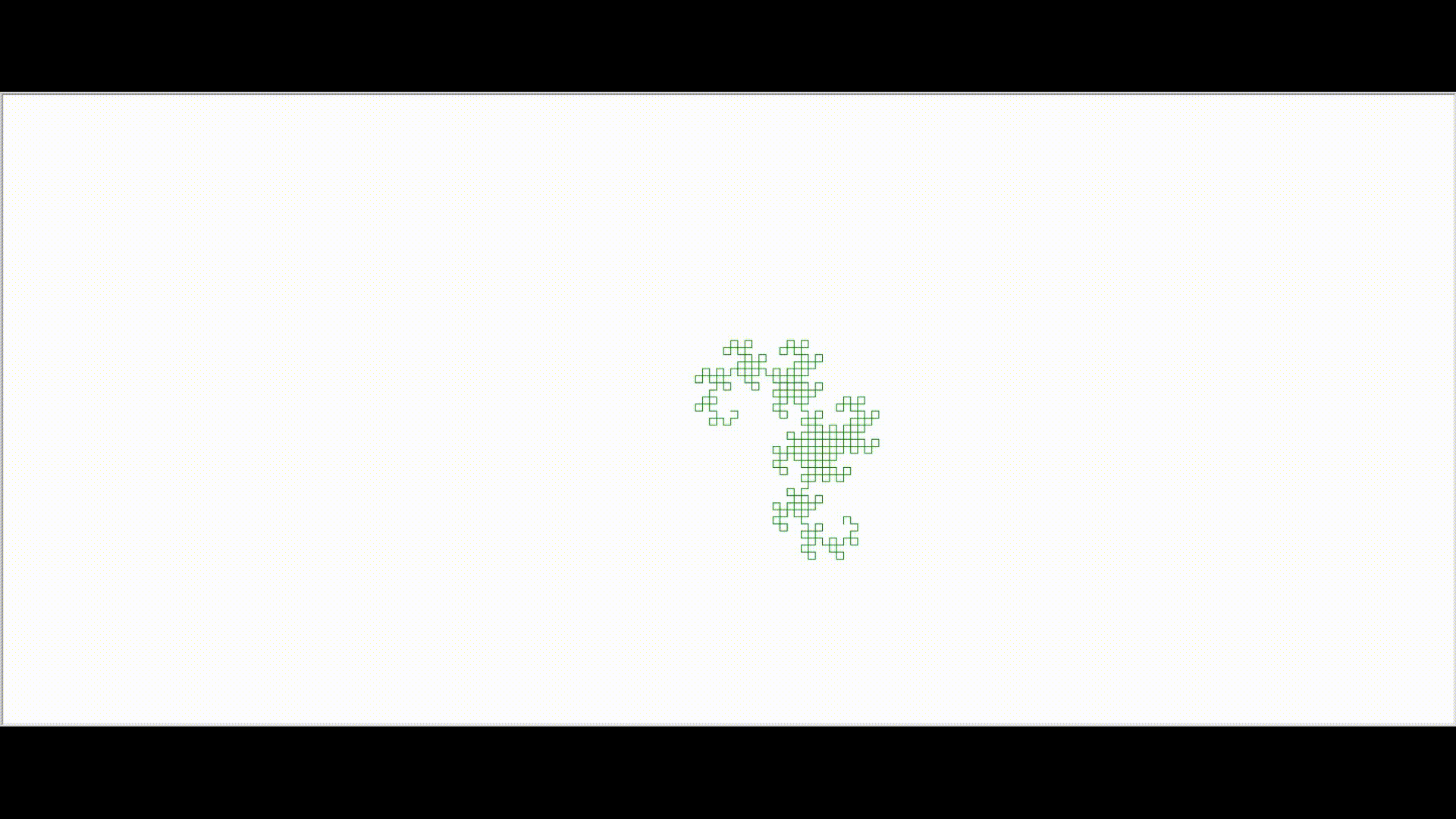
Dragon Curve using paper
These dragon curves can also be formed by Paper folding: The concept is so simple but the potential is amazing. Take a long strip of paper and fold it in half. You get a strip of paper with a fold in it! Refold the paper then fold it in half again. When you look inside you have two folds going in one direction and one fold going the other way. Refold and fold in half again and, when you unfold, you get even more folds, some going one way, some the other. Unfold the strip and make a firm crease along each of the fold lines, taking care to maintain the correct direction for the fold. Stand the strip on its edge, with each fold forming a 90 degree angle, and look down on it. You will see an intricate pattern of squares, and twists and turns. The strips get the name of Dragon Curves because, after a few folds, they start to take on the appearance of a dragon with large head, legs and tail. Numberphile explains Dragon Curve’s formation well in their video.You can also watch the Dragon curve transitions Here :
https://www.youtube.com/watch?v=3WBvS_n2oTY
Programming the Dragon Curve
PSEUDOCODE
? IMPORT TURTLE
? TURN TURTLE - RIGHT SIDE('r') #OLD PATTERN = 'r'
? NEW PATTERN = OLD PATTERN
? USER INPUT [ Number of Iterations(n), Segment size, Pen color & Background color ]
? CYCLE = 1
? WHILE CYCLE < ITERATION :
? FORM DRAGON CURVE L-SYSTEM
? STORE THE PATTERN OF 'l'/'r' in NEW PATTERN
? NEW PATTERN += OLD PATTERN
? OLD PATTERN = NEW PATTERN
? INCREMENT CYCLE
? USER INPUT [Whether to display 'r'/'l' Dragon curve L-system in console]
? INITIATE THE TURTLE TO DRAW [pencolor, bgcolor, draw right = segment size]
? ITERATE OVER FULL L SYSTEM FOR n ITERATIONS:
? IF CHAR == 'r'
? DRAW RIGHT(90)
? DRAW FORWARD(Segment Size)
? ELSE IF CHAR == 'l'
? DRAW LEFT(90)
? DRAW FORWARD(Segment Size)
? END
Python
import turtle
r = 'r'
l = 'l'
old = r
new = old
iteration = int(input('Enter iteration:'))
length = int(input('Enter length of each segment:'))
pencolor = input('Enter pen color:')
bgcolor = input('Enter background color:')
cycle = 1
while cycle<iteration:
new = (old) + (r)
old = old[::-1]
for char in range(0, len(old)):
if old[char] == r:
old = (old[:char])+ (l) + (old[char + 1:])
elif old[char] == l:
old = (old[:char]) + (r) + (old[char + 1:])
new = (new) + (old)
old = new
cycle = cycle + 1
printans = input('Display r/l form?(y/n):')
if printans =='y':
print(new)
turtle.ht()
turtle.speed(0)
turtle.color(pencolor)
turtle.bgcolor(bgcolor)
turtle.forward(length)
for char in range(0, len(new)):
if new[char] == (r):
turtle.right(90)
turtle.forward(length)
elif new[char] == (l):
turtle.left(90)
turtle.forward(length)
|
Output :
Get the codes of Dragon curve for different languages from rosettacode. It will give you great pleasure to check the fractals yourself. Also check, Project Euler : Problem 220 : Heighway Dragon. References:
Share your thoughts in the comments
Please Login to comment...