Python – Hilbert Curve using turtle
Last Updated :
04 Apr, 2023
Fractal is a curve or a figure which repeats itself. It comprises a recursive pattern that repeats itself up to a desired level of nesting. Turtle graphics are provided in the turtle module which is used for drawing various shapes and patterns in Python.
A Hilbert curve is a curve that is formed by connecting a sequence of U-shaped curves arranged and oriented in different directions. These U-shaped curves are placed at a certain step size distance apart.
Let us examine a Level-1 Hilbert Curve. The following steps will draw a simple U curve. Let y = 90 degree
- Rotate y degree towards the right
- Move step size
- Rotate y degree towards the left
- Move step size
- Rotate y degree towards the left
- Move step size
- Rotate y degree towards the right
Let us examine and try to understand the level-2 Hilbert Curve. Again, we assume that the turtle pointer points towards right initially. The following steps may be used to draw the curve:
- Rotate 90 degrees towards the right
- Create a hilbert curve at level 1 rotated by -y degrees (ie, y degrees in anticlockwise direction)
- Move step size
- Rotate y degrees towards the right
- Create a level 1 hilbert curve rotated by y degrees (ie, y degrees in clockwise direction)
- Rotate y degrees towards the left.
- Move step size
- Create a level 1 hilbert curve rotated by -y degrees
- Rotate y degrees towards the right

Turtle methods used in this section are as follows:
- forward(): Used for moving the turtle forward by a given distance in the direction of the turtle.
- backward(): Used for moving the turtle backward by a given distance in the direction of the turtle.
- left(): Used for rotating the turtle in the left direction by a specified angle.
- right(): Used for rotating the turtle in the right direction by a specified angle.
- goto(): Used for moving the turtle to the location specified ((x, y) coordinates).
- penup(): Used for specifying that no drawing will be made while moving.
- pendown(): Used for specifying that drawing will be made while moving.
- done(): Used to specify that the turtle work is completed.
Hibert Curve:
It is also called a peano or space-filling curve. It requires successive approximation. In the first approximation the square is divided into 4 quadrants and draw the curve that connects the center points of each. In the second approximation further, every quadrant is divided which cannot be the center of each.
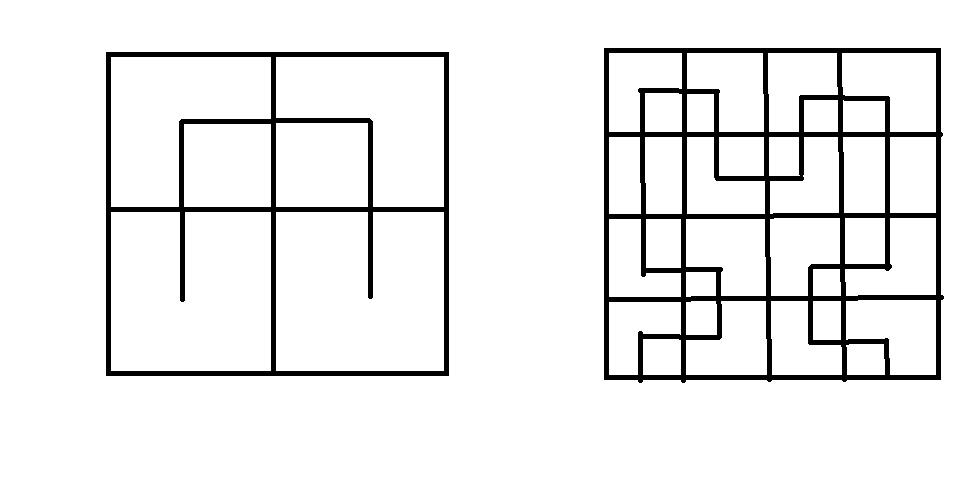
Hibert Curve
- There is no limit to the subdivision. Ideally length of the curve is infinite. With every subdivision the length Increase by 4
- The curve is equivalent to line. Its topological dimension is 1.
- Length of the curve changes by 4.
N = sDf
4 = 2Df
Df = 2 DT = 1 Df = 2
Df > DT
So if a line but folded such that it looks like a 2D object.
- Point sets, curves, and surfaces which has fractal dimension greater than the topological dimension are referred to as fractals.
- The curve generation starts with a square. In a first approximation, the square is divided into 4 quadrants and the curve joins the center of all quadrants by a straight line.
- .In the quadrants it is subdivided into 2*2 grids, ending in 16 squares. Curve visits the center of each small square in each quadrant before moving to the next quadrant
- In 16 squares it is subdivided into 2 * 2 grids, ending in 64 squares. Curve visits the center of each small square before moving to the higher-level quadrant.
- On applying this process continuously,
- The curve never crosses itself
- Curve gets closer to a square containing it
- With each subdivision, the length of the curve increases four times.
- There is no limit on depth and hence there is no limit on curve length.
Applications of Hibert Curve:
- It is used for Modelling natural structures like Geographic terrain, mountain, plant structure, clouds, vegetables etc.
- Space research.
- Study of convergence of iterative processes.
- Engineering and architecture.
- Medical science.
- Chemical processes.
- Medical diagnostic images.
- Fluid mechanics.
- Image compression and different Telecommunication purposes.
Code:
Python3
from turtle import *
def hilbert(level, angle, step):
if level == 0:
return
right(angle)
hilbert(level-1, -angle, step)
forward(step)
left(angle)
hilbert(level-1, angle, step)
forward(step)
hilbert(level-1, angle, step)
left(angle)
forward(step)
hilbert(level-1, -angle, step)
right(angle)
def main():
level = int(input())
size = 200
penup()
goto(-size / 2.0, size / 2.0)
pendown()
hilbert(level, 90, size/(2**level-1))
done()
if __name__ == '__main__':
main()
|
Share your thoughts in the comments
Please Login to comment...