Find Minimum Depth of a Binary Tree
Last Updated :
25 May, 2023
Given a binary tree, find its minimum depth. The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
For example, minimum depth of below Binary Tree is 2.
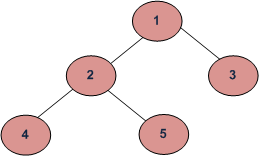
Note that the path must end on a leaf node. For example, the minimum depth of below Binary Tree is also 2.
10
/
5
Method 1: The idea is to traverse the given Binary Tree. For every node, check if it is a leaf node. If yes, then return 1. If not leaf node then if the left subtree is NULL, then recur for the right subtree. And if the right subtree is NULL, then recur for the left subtree. If both left and right subtrees are not NULL, then take the minimum of two depths.
Below is implementation of the above idea.
C++
#include<bits/stdc++.h>
using namespace std;
struct Node
{
int data;
struct Node* left, *right;
};
int minDepth(Node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
int l = INT_MAX, r = INT_MAX;
if (root->left)
l = minDepth(root->left);
if (root->right)
r = minDepth(root->right);
return min(l , r) + 1;
}
Node *newNode(int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return (temp);
}
int main()
{
Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout <<"The minimum depth of binary tree is : "<< minDepth(root);
return 0;
}
|
C
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int data;
struct Node *left, *right;
} Node;
int min(int num1, int num2)
{
return (num1 > num2) ? num2 : num1;
}
int minDepth(Node* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
int l = INT_MAX;
int r = INT_MIN;
if (root->left)
l = minDepth(root->left);
if (root->right)
r = minDepth(root->right);
return min(l, r) + 1;
}
Node* newNode(int data)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = data;
temp->left = temp->right = NULL;
return (temp);
}
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("The minimum depth of binary tree is : %d",
minDepth(root));
return 0;
}
|
Java
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
Node root;
int minimumDepth()
{
return minimumDepth(root);
}
int minimumDepth(Node root)
{
if (root == null)
return 0;
if (root.left == null && root.right == null)
return 1;
if (root.left == null)
return minimumDepth(root.right) + 1;
if (root.right == null)
return minimumDepth(root.left) + 1;
return Math.min(minimumDepth(root.left),
minimumDepth(root.right)) + 1;
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("The minimum depth of "+
"binary tree is : " + tree.minimumDepth());
}
}
|
Python3
class Node:
def __init__(self , key):
self.data = key
self.left = None
self.right = None
def minDepth(root):
if root is None:
return 0
if root.left is None and root.right is None:
return 1
if root.left is None:
return minDepth(root.right)+1
if root.right is None:
return minDepth(root.left) +1
return min(minDepth(root.left), minDepth(root.right))+1
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print (minDepth(root))
|
C#
using System;
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
public Node root;
public virtual int minimumDepth()
{
return minimumDepth(root);
}
public virtual int minimumDepth(Node root)
{
if (root == null)
{
return 0;
}
if (root.left == null && root.right == null)
{
return 1;
}
if (root.left == null)
{
return minimumDepth(root.right) + 1;
}
if (root.right == null)
{
return minimumDepth(root.left) + 1;
}
return Math.Min(minimumDepth(root.left), minimumDepth(root.right)) + 1;
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("The minimum depth of binary tree is : " + tree.minimumDepth());
}
}
|
Javascript
<script>
class Node {
constructor(item) {
this.data = item;
this.left = this.right = null;
}
}
let root;
function minimumDepth() {
return minimumDepth(root);
}
function minimumDepth( root) {
if (root == null)
return 0;
if (root.left == null && root.right == null)
return 1;
if (root.left == null)
return minimumDepth(root.right) + 1;
if (root.right == null)
return minimumDepth(root.left) + 1;
return Math.min(minimumDepth(root.left), minimumDepth(root.right)) + 1;
}
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write("The minimum depth of "
+ "binary tree is : " + minimumDepth(root));
</script>
|
Output
The minimum depth of binary tree is : 2
Time Complexity: O(n), as it traverses the tree only once.
Auxiliary Space: O(h), where h is the height of the tree, this space is due to the recursive call stack.
Method 2: The above method may end up with complete traversal of Binary Tree even when the topmost leaf is close to root. A Better Solution is to do Level Order Traversal. While doing traversal, returns depth of the first encountered leaf node.
Below is the implementation of this solution.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
Node(int d = 0)
: data{ d }
{
}
};
struct qItem {
Node* node;
int depth;
};
int minDepth(Node* root)
{
if (root == NULL)
return 0;
queue<qItem> q;
qItem qi = { root, 1 };
q.push(qi);
while (q.empty() == false) {
qi = q.front();
q.pop();
Node* node = qi.node;
int depth = qi.depth;
if (node->left == NULL && node->right == NULL)
return depth;
if (node->left != NULL) {
qi.node = node->left;
qi.depth = depth + 1;
q.push(qi);
}
if (node->right != NULL) {
qi.node = node->right;
qi.depth = depth + 1;
q.push(qi);
}
}
return 0;
}
Node* newNode(int data)
{
Node* temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right= new Node(5);
cout << minDepth(root);
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static class Node
{
int data;
Node left, right;
}
static class qItem
{
Node node;
int depth;
public qItem(Node node, int depth)
{
this.node = node;
this.depth = depth;
}
}
static int minDepth(Node root)
{
if (root == null)
return 0;
Queue<qItem> q = new LinkedList<>();
qItem qi = new qItem(root, 1);
q.add(qi);
while (q.isEmpty() == false)
{
qi = q.peek();
q.remove();
Node node = qi.node;
int depth = qi.depth;
if (node.left == null && node.right == null)
return depth;
if (node.left != null)
{
qi.node = node.left;
qi.depth = depth + 1;
q.add(qi);
}
if (node.right != null)
{
qi.node = node.right;
qi.depth = depth + 1;
q.add(qi);
}
}
return 0;
}
static Node newNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.left = temp.right = null;
return temp;
}
public static void main(String[] args)
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
System.out.println(minDepth(root));
}
}
|
Python3
class Node:
def __init__(self , data):
self.data = data
self.left = None
self.right = None
def minDepth(root):
if root is None:
return 0
q = []
q.append({'node': root , 'depth' : 1})
while(len(q)>0):
queueItem = q.pop(0)
node = queueItem['node']
depth = queueItem['depth']
if node.left is None and node.right is None:
return depth
if node.left is not None:
q.append({'node' : node.left , 'depth' : depth+1})
if node.right is not None:
q.append({'node': node.right , 'depth' : depth+1})
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print (minDepth(root))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class Node
{
public int data;
public Node left, right;
}
public class qItem
{
public Node node;
public int depth;
public qItem(Node node, int depth)
{
this.node = node;
this.depth = depth;
}
}
static int minDepth(Node root)
{
if (root == null)
return 0;
Queue<qItem> q = new Queue<qItem>();
qItem qi = new qItem(root, 1);
q.Enqueue(qi);
while (q.Count != 0)
{
qi = q.Peek();
q.Dequeue();
Node node = qi.node;
int depth = qi.depth;
if (node.left == null &&
node.right == null)
return depth;
if (node.left != null)
{
qi.node = node.left;
qi.depth = depth + 1;
q.Enqueue(qi);
}
if (node.right != null)
{
qi.node = node.right;
qi.depth = depth + 1;
q.Enqueue(qi);
}
}
return 0;
}
static Node newNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.left = temp.right = null;
return temp;
}
public static void Main(String[] args)
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
Console.WriteLine(minDepth(root));
}
}
|
Javascript
<script>
class Node
{
constructor(data)
{
this.data = data;
this.left = this.right = null;
}
}
class qItem
{
constructor(node,depth)
{
this.node = node;
this.depth = depth;
}
}
function minDepth(root)
{
if (root == null)
return 0;
let q = [];
let qi = new qItem(root, 1);
q.push(qi);
while (q.length != 0)
{
qi = q.shift();
let node = qi.node;
let depth = qi.depth;
if (node.left == null && node.right == null)
return depth;
if (node.left != null)
{
qi.node = node.left;
qi.depth = depth + 1;
q.push(qi);
}
if (node.right != null)
{
qi.node = node.right;
qi.depth = depth + 1;
q.push(qi);
}
}
return 0;
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
document.write(minDepth(root));
</script>
|
Time Complexity: O(n), where n is the number of nodes in the given binary tree. This is due to the fact that we are visiting each node once.
Auxiliary Space: O(n), as we need to store the elements in a queue for level order traversal.
Share your thoughts in the comments
Please Login to comment...