Snake and Ladder Problem
Last Updated :
18 Apr, 2024
Given a snake and ladder board, find the minimum number of dice throws required to reach the destination or last cell from the source or 1st cell. Basically, the player has total control over the outcome of the dice throw and wants to find out the minimum number of throws required to reach the last cell.
If the player reaches a cell which is the base of a ladder, the player has to climb up that ladder and if reaches a cell is the mouth of the snake, and has to go down to the tail of the snake without a dice throw.
Example:
Input:
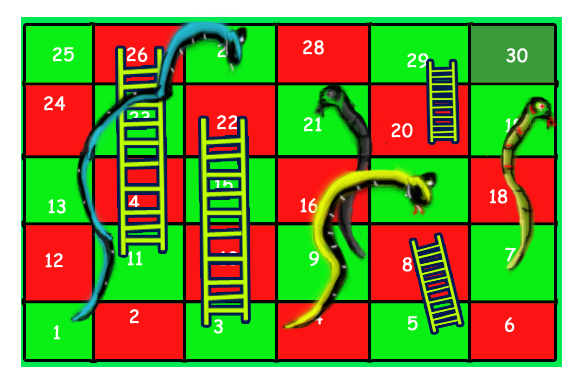
Output: 3
Explaination: Following are the steps:
- First throw two dice to reach cell number 3 and then ladder to reach 22
- Then throw 6 to reach 28.
- Finally through 2 to reach 30.
- There can be other solutions as well like (2, 2, 6), (2, 4, 4), (2, 3, 5).. etc.
The idea is to consider the given snake and ladder board as a directed graph with a number of vertices equal to the number of cells in the board. The problem reduces to finding the shortest path in a graph. Every vertex of the graph has an edge to next six vertices if the next 6 vertices do not have a snake or ladder. If any of the next six vertices has a snake or ladder, then the edge from the current vertex goes to the top of the ladder or tail of the snake. Since all edges are of equal weight, we can efficiently find the shortest path using Breadth-First Search of the graph.
Following is the implementation of the above idea.
C++
// C++ program to find minimum number of dice throws
// required to reach last cell from first cell of a given
// snake and ladder board
#include <iostream>
#include <queue>
using namespace std;
// An entry in queue used in BFS
struct queueEntry {
int v; // Vertex number
int dist; // Distance of this vertex from source
};
// This function returns minimum number of dice throws
// required to Reach last cell from 0'th cell in a snake and
// ladder game. move[] is an array of size N where N is no.
// of cells on board If there is no snake or ladder from
// cell i, then move[i] is -1 Otherwise move[i] contains
// cell to which snake or ladder at i takes to.
int getMinDiceThrows(int move[], int N)
{
// The graph has N vertices. Mark all the vertices as
// not visited
bool* visited = new bool[N];
for (int i = 0; i < N; i++)
visited[i] = false;
// Create a queue for BFS
queue<queueEntry> q;
// Mark the node 0 as visited and enqueue it.
visited[0] = true;
queueEntry s
= { 0, 0 }; // distance of 0't vertex is also 0
q.push(s); // Enqueue 0'th vertex
// Do a BFS starting from vertex at index 0
queueEntry qe; // A queue entry (qe)
while (!q.empty()) {
qe = q.front();
int v = qe.v; // vertex no. of queue entry
// If front vertex is the destination vertex,
// we are done
if (v == N - 1)
break;
// Otherwise dequeue the front vertex and enqueue
// its adjacent vertices (or cell numbers reachable
// through a dice throw)
q.pop();
for (int j = v + 1; j <= (v + 6) && j < N; ++j) {
// If this cell is already visited, then ignore
if (!visited[j]) {
// Otherwise calculate its distance and mark
// it as visited
queueEntry a;
a.dist = (qe.dist + 1);
visited[j] = true;
// Check if there a snake or ladder at 'j'
// then tail of snake or top of ladder
// become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.push(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
// Driver program to test methods of graph class
int main()
{
// Let us construct the board given in above diagram
int N = 30;
int moves[N];
for (int i = 0; i < N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
cout << "Min Dice throws required is "
<< getMinDiceThrows(moves, N);
return 0;
}
// Java program to find minimum number of dice
// throws required to reach last cell from first
// cell of a given snake and ladder board
import java.util.LinkedList;
import java.util.Queue;
public class SnakesLadder {
// An entry in queue used in BFS
static class qentry {
int v; // Vertex number
int dist; // Distance of this vertex from source
}
// This function returns minimum number of dice
// throws required to Reach last cell from 0'th cell
// in a snake and ladder game. move[] is an array of
// size N where N is no. of cells on board If there
// is no snake or ladder from cell i, then move[i]
// is -1 Otherwise move[i] contains cell to which
// snake or ladder at i takes to.
static int getMinDiceThrows(int move[], int n)
{
int visited[] = new int[n];
Queue<qentry> q = new LinkedList<>();
qentry qe = new qentry();
qe.v = 0;
qe.dist = 0;
// Mark the node 0 as visited and enqueue it.
visited[0] = 1;
q.add(qe);
// Do a BFS starting from vertex at index 0
while (!q.isEmpty()) {
qe = q.remove();
int v = qe.v;
// If front vertex is the destination
// vertex, we are done
if (v == n - 1)
break;
// Otherwise dequeue the front vertex and
// enqueue its adjacent vertices (or cell
// numbers reachable through a dice throw)
for (int j = v + 1; j <= (v + 6) && j < n;
++j) {
// If this cell is already visited, then
// ignore
if (visited[j] == 0) {
// Otherwise calculate its distance and
// mark it as visited
qentry a = new qentry();
a.dist = (qe.dist + 1);
visited[j] = 1;
// Check if there a snake or ladder at
// 'j' then tail of snake or top of
// ladder become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.add(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
public static void main(String[] args)
{
// Let us construct the board given in above diagram
int N = 30;
int moves[] = new int[N];
for (int i = 0; i < N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
System.out.println("Min Dice throws required is "
+ getMinDiceThrows(moves, N));
}
}
# Python3 program to find minimum number
# of dice throws required to reach last
# cell from first cell of a given
# snake and ladder board
# An entry in queue used in BFS
class QueueEntry(object):
def __init__(self, v=0, dist=0):
self.v = v
self.dist = dist
'''This function returns minimum number of
dice throws required to. Reach last cell
from 0'th cell in a snake and ladder game.
move[] is an array of size N where N is
no. of cells on board. If there is no
snake or ladder from cell i, then move[i]
is -1. Otherwise move[i] contains cell to
which snake or ladder at i takes to.'''
def getMinDiceThrows(move, N):
# The graph has N vertices. Mark all
# the vertices as not visited
visited = [False] * N
# Create a queue for BFS
queue = []
# Mark the node 0 as visited and enqueue it
visited[0] = True
# Distance of 0't vertex is also 0
# Enqueue 0'th vertex
queue.append(QueueEntry(0, 0))
# Do a BFS starting from vertex at index 0
qe = QueueEntry() # A queue entry (qe)
while queue:
qe = queue.pop(0)
v = qe.v # Vertex no. of queue entry
# If front vertex is the destination
# vertex, we are done
if v == N - 1:
break
# Otherwise dequeue the front vertex
# and enqueue its adjacent vertices
# (or cell numbers reachable through
# a dice throw)
j = v + 1
while j <= v + 6 and j < N:
# If this cell is already visited,
# then ignore
if visited[j] is False:
# Otherwise calculate its
# distance and mark it
# as visited
a = QueueEntry()
a.dist = qe.dist + 1
visited[j] = True
# Check if there a snake or ladder
# at 'j' then tail of snake or top
# of ladder become the adjacent of 'i'
a.v = move[j] if move[j] != -1 else j
queue.append(a)
j += 1
# We reach here when 'qe' has last vertex
# return the distance of vertex in 'qe
return qe.dist
# driver code
N = 30
moves = [-1] * N
# Ladders
moves[2] = 21
moves[4] = 7
moves[10] = 25
moves[19] = 28
# Snakes
moves[26] = 0
moves[20] = 8
moves[16] = 3
moves[18] = 6
print("Min Dice throws required is {0}".
format(getMinDiceThrows(moves, N)))
# This code is contributed by Ajitesh Pathak
// C# program to find minimum
// number of dice throws required
// to reach last cell from first
// cell of a given snake and ladder board
using System;
using System.Collections.Generic;
public class SnakesLadder {
// An entry in queue used in BFS
public class qentry {
public int v; // Vertex number
public int
dist; // Distance of this vertex from source
}
// This function returns minimum number of dice
// throws required to Reach last cell from 0'th cell
// in a snake and ladder game. move[] is an array of
// size N where N is no. of cells on board If there
// is no snake or ladder from cell i, then move[i]
// is -1 Otherwise move[i] contains cell to which
// snake or ladder at i takes to.
static int getMinDiceThrows(int[] move, int n)
{
int[] visited = new int[n];
Queue<qentry> q = new Queue<qentry>();
qentry qe = new qentry();
qe.v = 0;
qe.dist = 0;
// Mark the node 0 as visited and enqueue it.
visited[0] = 1;
q.Enqueue(qe);
// Do a BFS starting from vertex at index 0
while (q.Count != 0) {
qe = q.Dequeue();
int v = qe.v;
// If front vertex is the destination
// vertex, we are done
if (v == n - 1)
break;
// Otherwise dequeue the front vertex and
// enqueue its adjacent vertices (or cell
// numbers reachable through a dice throw)
for (int j = v + 1; j <= (v + 6) && j < n;
++j) {
// If this cell is already visited, then
// ignore
if (visited[j] == 0) {
// Otherwise calculate its distance and
// mark it as visited
qentry a = new qentry();
a.dist = (qe.dist + 1);
visited[j] = 1;
// Check if there a snake or ladder at
// 'j' then tail of snake or top of
// ladder become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.Enqueue(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
// Driver code
public static void Main(String[] args)
{
// Let us construct the board
// given in above diagram
int N = 30;
int[] moves = new int[N];
for (int i = 0; i < N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
Console.WriteLine("Min Dice throws required is "
+ getMinDiceThrows(moves, N));
}
}
// This code has been contributed by 29AjayKumar
<script>
// Javascript program to find minimum number of dice
// throws required to reach last cell from first
// cell of a given snake and ladder board
class qentry
{
constructor()
{
this.v = 0;
this.dist = 0;
}
}
// This function returns minimum number of dice
// throws required to Reach last cell from 0'th cell
// in a snake and ladder game. move[] is an array of
// size N where N is no. of cells on board If there
// is no snake or ladder from cell i, then move[i]
// is -1 Otherwise move[i] contains cell to which
// snake or ladder at i takes to.
function getMinDiceThrows(move,n)
{
let visited = new Array(n);
for(let i = 0; i < n; i++)
visited[i] = false;
let q = [];
let qe = new qentry();
qe.v = 0;
qe.dist = 0;
// Mark the node 0 as visited and enqueue it.
visited[0] = 1;
q.push(qe);
// Do a BFS starting from vertex at index 0
while (q.length != 0)
{
qe = q.shift();
let v = qe.v;
// If front vertex is the destination
// vertex, we are done
if (v == n - 1)
break;
// Otherwise dequeue the front vertex and
// enqueue its adjacent vertices (or cell
// numbers reachable through a dice throw)
for (let j = v + 1; j <= (v + 6) && j < n; ++j)
{
// If this cell is already visited, then ignore
if (visited[j] == 0)
{
// Otherwise calculate its distance and
// mark it as visited
let a = new qentry();
a.dist = (qe.dist + 1);
visited[j] = 1;
// Check if there a snake or ladder at 'j'
// then tail of snake or top of ladder
// become the adjacent of 'i'
if (move[j] != -1)
a.v = move[j];
else
a.v = j;
q.push(a);
}
}
}
// We reach here when 'qe' has last vertex
// return the distance of vertex in 'qe'
return qe.dist;
}
// Let us construct the board given in above diagram
let N = 30;
let moves = new Array(N);
for (let i = 0; i < N; i++)
moves[i] = -1;
// Ladders
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
// Snakes
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
document.write("Min Dice throws required is " +
getMinDiceThrows(moves, N));
// This code is contributed by avanitrachhadiya2155
</script>
OutputMin Dice throws required is 3
Time complexity: O(N) as every cell is added and removed only once from the queue. And a typical enqueue or dequeue operation takes O(1) time.
Auxiliary Space : O(N)
Snake and Ladder Problem using Recursion:
We can think of is recursion in which we will be going to each block, in this case, which is from 1 to 30, and keeping a count of a minimum number of throws of dice at block i and storing it in an array t.
So, basically, we will:
- Create an array, let’s say ‘t’, and initialize it with -1.
- Now we will call a recursive function from block 1, with variable let’s say ‘i’, and we will be incrementing this.
- In this we will define the base condition as whenever block number reaches 30 or beyond we will return 0 and we will also check if this block has been visited before, this we will do by checking the value of t[i], if this is -1 then it means its not visited and we move forward with the function else its visited and we will return value of t[i].
- After checking base cases we will initialize a variable ‘min’ with a max integer value.
- Now we will initiate a loop from 1 to 6, i.e the values of a dice, now for each iteration we will increase the value of i by the value of dice(eg: i+1,i+2….i+6) and we will check if any increased value has a ladder on it if there is then we will update the value of i to the end of the ladder and then pass the value to the recursive function, if there is no ladder then also we will pass the incremented value of i based on dice value to a recursive function, but if there is a snake then we won’t pass this value to recursive function as we want to reach the end as soon as possible, and the best of doing this would be not to be bitten by a snake. And we would be keep on updating the minimum value for variable ‘min’.
- Finally we will update t[i] with min and return t[i].
Below is the implementation of the above approach:
C++
#include <climits>
#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
int t[31];
// recursive function
int sol(int i, unordered_map<int, int>& h)
{
// base condition
if (i >= 30)
return 0;
// checking if block is already visited or
// not(memoization).
else if (t[i] != -1)
return t[i];
// initialising min as max int value
int min_value = INT_MAX;
// for loop for every dice value from 1 to 6
for (int j = 1; j <= 6; j++) {
// incrementing value of i with dice value i.e j
// taking new variable k
//->taking new variable so that we dont change i
// as we will need it again in another iteration
int k = i + j;
if (h.count(k) > 0) {
// checking if this is a snake or ladder
// if a snake then we continue as we dont
// need a snake
if (h[k] < k)
continue;
// updating if it's a ladder to ladder end value
k = h[k];
}
// updating min in every iteration for getting
// minimum throws from this particular block
min_value = min(min_value, sol(k, h) + 1);
}
// updating value of t[i] to min
// memoization
t[i] = min_value;
return t[i];
}
int min_throw(int n, vector<int> arr)
{
// Initialise an array t of length 31, we will use from
// index to 1 to 30
for (int i = 0; i < 31; i++) {
// initialising every index of t with -1
t[i] = -1;
}
// create a dictionary to store snakes and ladders start
// and end for better efficiency
unordered_map<int, int> h;
for (int i = 0; i < 2 * n; i += 2) {
// store start as key and end as value
h[arr[i]] = arr[i + 1];
}
// final ans
return sol(1, h);
}
int main()
{
// Given a 5x6 snakes and ladders board
// You are given an integer N denoting the total
// number of snakes and ladders and a list arr[]
// of 2*N size where 2*i and (2*i + 1)th values
// denote the starting and ending point respectively
// of ith snake or ladder
int N = 8;
vector<int> arr{ 3, 22, 5, 8, 11, 26, 20, 29,
17, 4, 19, 7, 27, 1, 29, 9 };
cout << "Min Dice throws required is "
<< min_throw(N, arr) << endl;
return 0;
}
// This code is contributed by sanjanasikarwar24
/*package whatever //do not write package name here */
import java.io.*;
import java.util.*;
class GFG {
// Initialise an array t of length 31, we will use from
// index to 1 to 30
static int[] t = new int[31];
static int minThrow(int n, int arr[])
{
// code here
for (int i = 0; i < 31; i++) {
// initialising every index of t with -1
t[i] = -1;
}
// create hashmap to store snakes and ladders start
// and end for better efficiency
HashMap<Integer, Integer> h = new HashMap<>();
for (int i = 0; i < 2 * n; i = i + 2) {
// store start as key and end as value
h.put(arr[i], arr[i + 1]);
}
// final ans
return sol(1, h);
}
// recursive function
static int sol(int i, HashMap<Integer, Integer> h)
{
// base condintion
if (i >= 30)
return 0;
// checking if block is already visited or
// not(memoization).
else if (t[i] != -1)
return t[i];
// initialising min as max int value
int min = Integer.MAX_VALUE;
// for loop for every dice value from 1 to 6
for (int j = 1; j <= 6; j++) {
// incrementing value of i with dice value i.e j
// taking new variable k
//->taking new variable so that we dont change i
// as we will need it again in another iteration
int k = i + j;
if (h.containsKey(k)) {
// checking if this is a snake of ladder
// if a snake then we continue as we dont
// need a snake
if (h.get(k) < k)
continue;
// updating if its a ladder to ladder end
// value
k = h.get(k);
}
// updating min in every iteration for getting
// minimum throws from this particular block
min = Math.min(min, sol(k, h) + 1);
}
// updating value of t[i] to min
// memoization
t[i] = min;
return t[i];
}
// main
public static void main(String[] args)
{
// Given a 5x6 snakes and ladders board
// You are given an integer N denoting the total
// number of snakes and ladders and an array arr[]
// of 2*N size where 2*i and (2*i + 1)th values
// denote the starting and ending point respectively
// of ith snake or ladder
int N = 8;
int[] arr = new int[2 * N];
arr[0] = 3;
arr[1] = 22;
arr[2] = 5;
arr[3] = 8;
arr[4] = 11;
arr[5] = 26;
arr[6] = 20;
arr[7] = 29;
arr[8] = 17;
arr[9] = 4;
arr[10] = 19;
arr[11] = 7;
arr[12] = 27;
arr[13] = 1;
arr[14] = 29;
arr[15] = 9;
System.out.println("Min Dice throws required is "
+ minThrow(N, arr));
}
}
from typing import List, Dict
def min_throw(n: int, arr: List[int]) -> int:
# Initialise an array t of length 31, we will use from
# index to 1 to 30
t = [-1] * 31
# create a dictionary to store snakes and ladders start
# and end for better efficiency
h = {}
for i in range(0, 2 * n, 2):
# store start as key and end as value
h[arr[i]] = arr[i + 1]
# final ans
return sol(1, h, t)
# recursive function
def sol(i: int, h: Dict[int, int], t: List[int]) -> int:
# base condition
if i >= 30:
return 0
# checking if block is already visited or
# not(memoization).
elif t[i] != -1:
return t[i]
# initialising min as max int value
min_value = float("inf")
# for loop for every dice value from 1 to 6
for j in range(1, 7):
# incrementing value of i with dice value i.e j
# taking new variable k
# ->taking new variable so that we dont change i
# as we will need it again in another iteration
k = i + j
if k in h:
# checking if this is a snake or ladder
# if a snake then we continue as we dont
# need a snake
if h[k] < k:
continue
# updating if it's a ladder to ladder end value
k = h[k]
# updating min in every iteration for getting
# minimum throws from this particular block
min_value = min(min_value, sol(k, h, t) + 1)
# updating value of t[i] to min
# memoization
t[i] = min_value
return t[i]
# Given a 5x6 snakes and ladders board
# You are given an integer N denoting the total
# number of snakes and ladders and a list arr[]
# of 2*N size where 2*i and (2*i + 1)th values
# denote the starting and ending point respectively
# of ith snake or ladder
N = 8
arr = [3, 22, 5, 8, 11, 26, 20, 29, 17, 4, 19, 7, 27, 1, 29, 9]
print("Min Dice throws required is", min_throw(N, arr))
# This code is contributed by sanjanasikarwar24
using System;
using System.Collections.Generic;
class GFG {
static int[] t=new int[31];
// recursive function
static int sol(int i, Dictionary<int, int> h)
{
// base condition
if (i >= 30)
return 0;
// checking if block is already visited or
// not(memoization).
else if (t[i] != -1)
return t[i];
// initialising min as max int value
int min_value =Int32.MaxValue;
;
// for loop for every dice value from 1 to 6
for (int j = 1; j <= 6; j++) {
// incrementing value of i with dice value i.e j
// taking new variable k
//->taking new variable so that we dont change i
// as we will need it again in another iteration
int k = i + j;
if (h.ContainsKey(k)) {
// checking if this is a snake or ladder
// if a snake then we continue as we dont
// need a snake
if (h[k] < k)
continue;
// updating if it's a ladder to ladder end value
k = h[k];
}
// updating min in every iteration for getting
// minimum throws from this particular block
min_value = Math.Min(min_value, sol(k, h) + 1);
}
// updating value of t[i] to min
// memoization
t[i] = min_value;
return t[i];
}
static int min_throw(int n, List<int> arr)
{
// Initialise an array t of length 31, we will use from
// index to 1 to 30
for (int i = 0; i < 31; i++) {
// initialising every index of t with -1
t[i] = -1;
}
// create a dictionary to store snakes and ladders start
// and end for better efficiency
Dictionary<int, int> h= new Dictionary<int, int>();
for (int i = 0; i < 2 * n; i += 2) {
// store start as key and end as value
h.Add(arr[i], arr[i + 1]);
}
// final ans
return sol(1, h);
}
public static void Main()
{
// Given a 5x6 snakes and ladders board
// You are given an integer N denoting the total
// number of snakes and ladders and a list arr[]
// of 2*N size where 2*i and (2*i + 1)th values
// denote the starting and ending point respectively
// of ith snake or ladder
int N = 8;
List<int> arr=new List<int>{ 3, 22, 5, 8, 11, 26, 20, 29,
17, 4, 19, 7, 27, 1, 29, 9 };
Console.Write("Min Dice throws required is "+ min_throw(N, arr));
}
}
let t=new Array(31);
// recursive function
function sol(i, h)
{
// base condition
if (i >= 30)
return 0;
// checking if block is already visited or
// not(memoization).
else if (t[i] != -1)
return t[i];
// initialising min as max int value
let min_value = Number.MAX_SAFE_INTEGER;
// for loop for every dice value from 1 to 6
for (let j = 1; j <= 6; j++) {
// incrementing value of i with dice value i.e j
// taking new variable k
//->taking new variable so that we dont change i
// as we will need it again in another iteration
let k = i + j;
if (h.has(k)) {
// checking if this is a snake or ladder
// if a snake then we continue as we dont
// need a snake
if (h.get(k) < k)
continue;
// updating if it's a ladder to ladder end value
k = h.get(k);
}
// updating min in every iteration for getting
// minimum throws from this particular block
min_value = Math.min(min_value, sol(k, h) + 1);
}
// updating value of t[i] to min
// memoization
t[i] = min_value;
return t[i];
}
function min_throw(n, arr)
{
// Initialise an array t of length 31, we will use from
// index to 1 to 30
for (let i = 0; i < 31; i++) {
// initialising every index of t with -1
t[i] = -1;
}
// create a dictionary to store snakes and ladders start
// and end for better efficiency
let h=new Map();
for (let i = 0; i < 2 * n; i += 2) {
// store start as key and end as value
h.set(arr[i],arr[i + 1]);
}
// final ans
return sol(1, h);
}
// Given a 5x6 snakes and ladders board
// You are given an integer N denoting the total
// number of snakes and ladders and a list arr[]
// of 2*N size where 2*i and (2*i + 1)th values
// denote the starting and ending point respectively
// of ith snake or ladder
let N = 8;
let arr=[ 3, 22, 5, 8, 11, 26, 20, 29,
17, 4, 19, 7, 27, 1, 29, 9 ];
console.log("Min Dice throws required is "+ min_throw(N, arr));
OutputMin Dice throws required is 3
Time complexity: O(N).
Auxiliary Space O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...