Find all distinct subsets of a given set using BitMasking Approach

Given an array of integers arr[], The task is to find all its subsets. The subset can not contain duplicate elements, so any repeated subset should be considered only once in the output.

Examples:

Input: S = {1, 2, 2}
Output: {}, {1}, {2}, {1, 2}, {2, 2}, {1, 2, 2}
Explanation: The total subsets of given set are – {}, {1}, {2}, {2}, {1, 2}, {1, 2}, {2, 2}, {1, 2, 2}
Here {2} and {1, 2} are repeated twice so they are considered only once in the output
Input: S = {1, 2}
Output: {}, {1}, {2}, {1, 2}
Explanation: The total subsets of given set are – {}, {1}, {2}, {1, 2}

BRUTE METHOD:

Intuition:
We do this problem by using the backtracking approach.
we declare a arraylist to store all the subsets generated.
We sort the array in order to skip repeated subsets as it should be unique.
then we pick a particular element or not pick from the array and we generate the subsets.
atlast we add it in the final list and return it.

Implementation:

Java

// Java program to find all subsets of given set. Any
// repeated subset is considered only once in the output
import java.io.*;
import java.util.*;
 
class GFG {
    public static void
    findSubsets(int ind, int[] nums, ArrayList<Integer> ds,
                ArrayList<ArrayList<Integer> > ansList)
    {
        ansList.add(new ArrayList<>(ds));
        for (int i = ind; i < nums.length; i++) {
            if (i != ind && nums[i] == nums[i - 1])
                continue;
 
            ds.add(nums[i]);
            findSubsets(i + 1, nums, ds, ansList);
            ds.remove(ds.size() - 1);
        }
    }
    public static ArrayList<ArrayList<Integer> >
    AllSubsets(int arr[], int n)
    {
        // your code here
        Arrays.sort(arr);
        ArrayList<ArrayList<Integer> > ansList
            = new ArrayList<>();
        findSubsets(0, arr, new ArrayList<>(), ansList);
 
        return ansList;
    }
    public static void main(String[] args)
    {
        int[] set = { 10, 12, 12 };
        System.out.println(AllSubsets(set, 3));
    }
}
// This code is contributed by Raunak Singh

Output

[[], [10], [10, 12], [10, 12, 12], [12], [12, 12]]

Time Complexity: O(2^N * N) since we are generating every subset

Auxiliary Space: O(2^N)

Prerequisite: Power Set

Approach: Below is the idea to solve the problem:

The idea is to use a bit-mask pattern to generate all the combinations as discussed in post. To avoid printing duplicate subsets construct a string out of given subset such that subsets having similar elements will result in same string. Maintain a list of such unique strings and finally decode all such string to print its individual elements.

Illustration :

S = {1, 2, 2}
The binary digits from 0 to 7 are
0 –> 000 –> number formed with no setbits –> { }
1 –> 001 –> number formed with setbit at position 0 –> { 1 }
2 –> 010 –> number formed with setbit at position 1 –> { 2 }
3 –> 011 –> number formed with setbit at position 0 and 1 –> { 1 , 2 }
4 –> 100 –> number formed with setbit at position 2 –> { 2 }
5 –> 101 –> number formed with setbit at position 0 and 2 –> { 1 , 2}
6 –> 110 –> number formed with setbit at position 1 and 2 –> { 2 , 2}
7 –> 111 –> number formed with setbit at position 0 , 1 and 2 –> {1 , 2 , 2}
After removing duplicates final result will be { }, { 1 }, { 2 }, { 1 , 2 }, { 2 , 2 }, { 1 , 2 , 2}

Note: This method will only work on sorted arrays.

Follow the below steps to Implement the idea:

Initialize a variable pow_set_size as 2 raise to size of array and a vector of vector ans to store all subsets.
Iterate over all bitmasks from 0 to pow_set_size – 1.
- For every bitmask include the elements of array of indices where bits are set into a subset vector.
- If this subset doesn’t already exist then push the subset in the ans vector.
Return ans.

Below is the implementation of the above approach:

C++14

// C++ program to find all subsets of given set. Any
// repeated subset is considered only once in the output
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find all subsets of given set. Any repeated
// subset is considered only once in the output
vector<vector<int> > findPowerSet(vector<int>& nums)
{
    // Size of array to set bit
    int bits = nums.size();
 
    // Total number of subsets = pow(2,
    // sizeof(arr))
    unsigned int pow_set_size = pow(2, bits);
 
    // Sort to avoid adding permutation of
    // the substring
    sort(nums.begin(), nums.end());
    vector<vector<int> > ans;
 
    // To store subset as a list to
    // avoid adding exact duplicates
    vector<string> list;
 
    // Counter 000..0 to 111..1
    for (int counter = 0; counter < pow_set_size;
         counter++) {
        vector<int> subset;
        string temp = "";
 
        // Check for the current bit in the counter
        for (int j = 0; j < bits; j++) {
            if (counter & (1 << j)) {
                subset.push_back(nums[j]);
 
                // Add special character to separate
                // integers
                temp += to_string(nums[j]) + '$';
            }
        }
 
        if (find(list.begin(), list.end(), temp)
            == list.end()) {
            ans.push_back(subset);
            list.push_back(temp);
        }
    }
 
    return ans;
}
 
// Driver code
int main()
{
    vector<int> arr{ 10, 12, 12 };
 
    vector<vector<int> > power_set = findPowerSet(arr);
 
    for (int i = 0; i < power_set.size(); i++) {
        for (int j = 0; j < power_set[i].size(); j++)
            cout << power_set[i][j] << " ";
        cout << endl;
    }
 
    return 0;
}
// this code is contributed by prophet1999

Java

// Java program to find all subsets of given set. Any
// repeated subset is considered only once in the output
import java.io.*;
import java.util.*;
 
public class GFG {
 
    // Function to find all subsets of given set. Any
    // repeated subset is considered only once in the output
    static void printPowerSet(int[] set, int set_size)
    {
 
        ArrayList<String> subset = new ArrayList<String>();
 
        /*set_size of power set of a set
        with set_size n is (2**n -1)*/
        long pow_set_size = (long)Math.pow(2, set_size);
        int counter, j;
 
        /*Run from counter 000..0 to
        111..1*/
        for (counter = 0; counter < pow_set_size;
             counter++) {
            String temp = "";
            for (j = 0; j < set_size; j++) {
                /* Check if jth bit in the
                counter is set If set then
                print jth element from set */
                if ((counter & (1 << j)) > 0)
                    temp
                        += (Integer.toString(set[j]) + '$');
            }
 
            if (!subset.contains(temp)
                && temp.length() > 0) {
                subset.add(temp);
            }
        }
 
        for (String s : subset) {
            s = s.replace('$', ' ');
            System.out.println(s);
        }
    }
 
    // Driver program to test printPowerSet
    public static void main(String[] args)
    {
        int[] set = { 10, 12, 12 };
        printPowerSet(set, 3);
    }
}
 
// This code is contributed by Aditya Patil.

Python3

# Python3 program to find all subsets of
# given set. Any repeated subset is
# considered only once in the output
 
 
def printPowerSet(arr, n):
 
    # Function to find all subsets of given set.
    # Any repeated subset is considered only
    # once in the output
    _list = []
 
    # Run counter i from 000..0 to 111..1
    for i in range(2**n):
        subset = ""
 
        # consider each element in the set
        for j in range(n):
 
            # Check if jth bit in the i is set.
            # If the bit is set, we consider
            # jth element from set
            if (i & (1 << j)) != 0:
                subset += str(arr[j]) + "|"
 
        # if subset is encountered for the first time
        # If we use set<string>, we can directly insert
        if subset not in _list and len(subset) > 0:
            _list.append(subset)
 
    # consider every subset
    for subset in _list:
 
        # split the subset and print its elements
        arr = subset.split('|')
        for string in arr:
            print(string, end=" ")
        print()
 
 
# Driver Code
if __name__ == '__main__':
    arr = [10, 12, 12]
    n = len(arr)
    printPowerSet(arr, n)
 
# This code is contributed by vibhu4agarwal

C#

// C# program to find all subsets of given set. Any
// repeated subset is considered only once in the output
using System;
using System.Collections.Generic;
 
public class GFG {
 
  // Function to find all subsets of given set. Any
  // repeated subset is considered only once in the output
  static void printPowerSet(int[] set, int set_size)
  {
 
    List<string> subset = new List<string>();
 
    /*set_size of power set of a set
        with set_size n is (2**n -1)*/
    long pow_set_size = (long)Math.Pow(2, set_size);
    int counter, j;
 
    /*Run from counter 000..0 to
        111..1*/
    for (counter = 0; counter < pow_set_size;
         counter++) {
      string temp = "";
      for (j = 0; j < set_size; j++) {
        /* Check if jth bit in the
                counter is set If set then
                print jth element from set */
        if ((counter & (1 << j)) > 0)
          temp
          += (Convert.ToString(set[j]) + ' ');
      }
 
      if (!subset.Contains(temp) && temp.Length > 0) {
        subset.Add(temp);
      }
    }
 
    foreach(string s in subset)
    {
      s.Replace('$', ' ');
      Console.WriteLine(s);
    }
  }
 
  // Driver program to test printPowerSet
  public static void Main(string[] args)
  {
    int[] set = { 10, 12, 12 };
    printPowerSet(set, 3);
  }
}
 
// This code is contributed by ishankhandelwals.

Javascript

<script>
        // JavaScript program to find all subsets of given set. Any
        // repeated subset is considered only once in the output
 
        // Function to find all subsets of given set. Any repeated
        // subset is considered only once in the output
        const findPowerSet = (nums) => {
            let bits = nums.length;     // size of array to set bit
            let pow_set_size = Math.pow(2, bits);     // total number of subsets = pow(2, sizeof(arr))
            nums.sort();     // sort to avoid adding permutation of the substring
            let ans = [];
            let list = [];     // to store subset as a list to avoid adding exact duplicates
 
 
            // counter 000..0 to 111..1
            for (let counter = 0; counter < pow_set_size; counter++) {
                let subset = [];
                let temp = "";
 
                // check for the current bit in the counter
                for (let j = 0; j < bits; j++) {
                    if (counter & (1 << j)) {
                        subset.push(nums[j]);
                        // add special character to separate integers
                        temp += nums[j].toString() + '$';
                    }
                }
 
                if (list.indexOf(temp) == -1) {
                    ans.push(subset);
                    list.push(temp);
                }
            }
 
            return ans;
        }
 
        // Driver code
 
        let arr = [10, 12, 12];
 
        let power_set = findPowerSet(arr);
 
        for (let i = 0; i < power_set.length; i++) {
            for (let j = 0; j < power_set[i].length; j++)
                document.write(`${power_set[i][j]} `);
            document.write("<br/>");
        }
 
    // This code is contributed by rakeshsahni
 
    </script>

Output

Time Complexity: O(N*2^N)
Auxiliary Space: O(N*N)

Analysis:

If 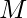$M$ is the total number of steps in the code, then the loop to generate all binary combinations runs till, and then the inner loop run till log(i).
Hence, $M = \sum_{i=1}^{2^n}{log[i]}$ , Raising to the power of two on both sides
$2^M = 2^{\sum_{i=1}^{2^N}{log[i]}} = \prod_{i=1}^{2^N}{2^{log[i]}} = \prod_{i=1}^{2^N}{i} = (2^N)!$
Using log on both sides and applying Sterling’s approximation,
$M = log(2^{N}!) \approx N2^N - 2^N = N2^N$
Hence the time complexity is $O(N*2^N)$