Print all subsets of a given Set or Array
Last Updated :
22 Sep, 2023
Given an array Arr[] of size N, print all the subsets of the array.
Subset: A subset of an array is a tuple that can be obtained from the array by removing some (possibly all) elements of it
Example:
Input: N = 3, Arr = [1, 2, 3]
Output: {}
{1}
{1, 2}
{1, 2, 3}
{1, 3}
{2}
{2, 3}
{3}
Explanation: These are all the subsets that can be formed from the given array, it can be proven that no other subset exists other than the given output.
Input: N = 2, Arr = [2, 4]
Output: {}
{2}
{2, 4}
{4}
Explanation: These are all the subsets that can be formed from the given array, it can be proven that no other subset exists other than the given output.
How many Subsets are possible for an Array of size ‘N’ ?
Before jumping into the solution, can we observe some kind of relation between the size of array N and the number of subsets formed by that array? The answer is YES, there exists a relation that is given by the following formula:
Number of Subsets of an array of size N = 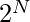
Proof: For each element of the array we have 2 choices:
- Choice 1: Include it into the subset.
- Choice 2: Exclude it from the subset.
Since, each element has 2 choice to contribute into the subset and we have total N elements, therefore total subsets = 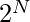
Let’s see how can we construct our solution from this observation.
Printing all subsets using Backtracking:
As mentioned above, for each element there two options, either include it into subset or exclude it. Backtracking algorithm can allow us to explore all possible choices one by one recursively.
State Space Tree for printing all subsets using Backtracking:
Suppose an array of size 3 having elements {1, 2, 3}, the state space tree can be constructed as below:

Follow the the steps below to implement the above idea:
- It starts with an empty subset and adds it to the result list.
- It iterates through the elements of the input vector:
- Includes the current element in the subset.
- Recursively calls itself with the updated subset and the next index.
- Excludes the current element from the subset (backtracks).
Below are the implementation of the above approach:
C++
#include <iostream>
#include <vector>
using namespace std;
void calcSubset(vector<int>& A, vector<vector<int> >& res,
vector<int>& subset, int index)
{
res.push_back(subset);
for (int i = index; i < A.size(); i++) {
subset.push_back(A[i]);
calcSubset(A, res, subset, i + 1);
subset.pop_back();
}
}
vector<vector<int> > subsets(vector<int>& A)
{
vector<int> subset;
vector<vector<int> > res;
int index = 0;
calcSubset(A, res, subset, index);
return res;
}
int main()
{
vector<int> array = { 1, 2, 3 };
vector<vector<int> > res = subsets(array);
for (int i = 0; i < res.size(); i++) {
for (int j = 0; j < res[i].size(); j++)
cout << res[i][j] << " ";
cout << endl;
}
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
public class Subsets {
public static void calcSubset(List<Integer> A,
List<List<Integer> > res,
List<Integer> subset,
int index)
{
res.add(new ArrayList<>(subset));
for (int i = index; i < A.size(); i++) {
subset.add(A.get(i));
calcSubset(A, res, subset, i + 1);
subset.remove(subset.size() - 1);
}
}
public static List<List<Integer> >
subsets(List<Integer> A)
{
List<Integer> subset = new ArrayList<>();
List<List<Integer> > res = new ArrayList<>();
int index = 0;
calcSubset(A, res, subset, index);
return res;
}
public static void main(String[] args)
{
List<Integer> array = List.of(1, 2, 3);
List<List<Integer> > res = subsets(array);
for (List<Integer> subset : res) {
for (Integer num : subset) {
System.out.print(num + " ");
}
System.out.println();
}
}
}
|
Python
def calcSubset(A, res, subset, index):
res.append(subset[:])
for i in range(index, len(A)):
subset.append(A[i])
calcSubset(A, res, subset, i + 1)
subset.pop()
def subsets(A):
subset = []
res = []
index = 0
calcSubset(A, res, subset, index)
return res
if __name__ == "__main__":
array = [1, 2, 3]
res = subsets(array)
for subset in res:
print(*subset)
|
C#
using System;
using System.Collections.Generic;
class Program {
static void CalcSubset(List<int> A,
List<List<int> > res,
List<int> subset, int index)
{
res.Add(new List<int>(subset));
for (int i = index; i < A.Count; i++) {
subset.Add(A[i]);
CalcSubset(A, res, subset, i + 1);
subset.RemoveAt(subset.Count - 1);
}
}
static List<List<int> > Subsets(List<int> A)
{
List<int> subset = new List<int>();
List<List<int> > res = new List<List<int> >();
int index = 0;
CalcSubset(A, res, subset, index);
return res;
}
static void Main(string[] args)
{
List<int> array = new List<int>{ 1, 2, 3 };
List<List<int> > res = Subsets(array);
foreach(List<int> subset in res)
{
Console.WriteLine(string.Join(" ", subset));
}
}
}
|
Javascript
function calcSubset(A, res, subset, index) {
res.push([...subset]);
for (let i = index; i < A.length; i++) {
subset.push(A[i]);
calcSubset(A, res, subset, i + 1);
subset.pop();
}
}
function subsets(A) {
const subset = [];
const res = [];
let index = 0;
calcSubset(A, res, subset, index);
return res;
}
function main() {
const array = [1, 2, 3];
const res = subsets(array);
for (let i = 0; i < res.length; i++) {
console.log(res[i].join(' '));
}
}
main();
|
Output
1
1 2
1 2 3
1 3
2
2 3
3
Complexity Analysis:
- Time Complexity: O(2^N), where n is the size of given array.
- Auxiliary Space:
- O(N) : if we only print our subsets, there will at max N recursion stack
- O(2^N) : if we would store all the subsets we will need 2^N memory blocks to store each subset
Printing all Subsets Using Bit Manipulation
This approach is simpler compared to backtracking, as it just requires basic knowledge of bits.
Observation: A bit can be either 0 or 1. What can we deduce from this?
Since, each element has only two choices i.e. either get included or get excluded. Assign these choices to a bit representation such that:
0 means Excluded
1 means Included
i’th bit represents i’th element of the array
Now let’s say, there are N elements in the array. This array will have 2^N subsets. These subsets can be uniquely expressed in form of Bit representation of number from 0 to (2^N)-1.
Example: If elements in an array of size 2 = {A, B}
All the subsets of this array form the bit representation of number from 0 to (2^2)-1 i.e. 0 to 3
0 = 00 => A excluded, B excluded => { empty }
1 = 01 => A excluded, B included => { B }
2 = 10 => A included, B excluded => { A }
3 = 11 => A included, B included=> { A, B }
Illustration:
Suppose given an array of size 3 = {1, 2, 3}. Generate all the subsets using bit manipulation as shown in the image below:

Below are the step-by-step approach:
- Iterate numbers from 0 to (2^n)-1
- Generate binary representation of that number and include the elements of array as per below cases:
- If the i’th bit is 1, then include i’th element of the array into current subset
- If the i’th bit is 0, do nothing and continue.
- Each bit representation of the number will give a unique subset.
Below are the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void findSubsets(int nums[], int n)
{
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if ((i & (1 << j)) != 0) {
cout << nums[j] << " ";
}
}
cout << endl;
}
}
int main()
{
int arr[] = { 1, 2, 3 };
int n = sizeof(arr)/sizeof(arr[0]);
findSubsets(arr, n);
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
public static void findSubsets(int[] nums)
{
int n = nums.length;
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if ((i & (1 << j)) != 0) {
System.out.print(nums[j] + " ");
}
}
System.out.println();
}
}
public static void main(String[] args)
{
int[] arr = new int[] { 1, 2, 3 };
findSubsets(arr);
}
}
|
Python3
def findSubsets(nums, n):
for i in range(1 << n):
for j in range(n):
if (i & (1 << j)) != 0:
print(nums[j], end=" ")
print()
arr = [1, 2, 3]
n = len(arr)
findSubsets(arr, n)
|
C#
using System;
public class GFG {
static void FindSubsets(int[] nums)
{
int n = nums.Length;
for (int i = 0; i < (1 << n); i++) {
for (int j = 0; j < n; j++) {
if ((i & (1 << j)) != 0) {
Console.Write(nums[j] + " ");
}
}
Console.WriteLine();
}
}
public static void Main(string[] args)
{
int[] arr = { 1, 2, 3 };
FindSubsets(arr);
}
}
|
Javascript
function findSubsets(nums, n) {
for (let i = 0; i < (1 << n); i++) {
for (let j = 0; j < n; j++) {
if ((i & (1 << j)) !== 0) {
process.stdout.write(nums[j] + " ");
}
}
console.log();
}
}
let arr = [1, 2, 3];
let n = arr.length;
findSubsets(arr, n);
|
Output
1
2
1 2
3
1 3
2 3
1 2 3
Complexity Analysis:
- Time Complexity: O(2^N), where N is the size of given array.
- Auxiliary Space:
- O(1) : if we only print our subsets
- O(2^N) : if we would store all the subsets we will need 2^N memory blocks to store each subset
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...