Fibonacci Heap | Set 1 (Introduction)
Last Updated :
19 Jun, 2023
INTRODUCTION:
- A Fibonacci heap is a data structure used for implementing priority queues. It is a type of heap data structure, but with several improvements over the traditional binary heap and binomial heap data structures.
- The key advantage of a Fibonacci heap over other heap data structures is its fast amortized running time for operations such as insert, merge and extract-min, making it one of the most efficient data structures for these operations. The running time of these operations in a Fibonacci heap is O(1) for insert, O(log n) for extract-min and O(1) amortized for merge.
- A Fibonacci heap is a collection of trees, where each tree is a heap-ordered multi-tree, meaning that each tree has a single root node with its children arranged in a heap-ordered manner. The trees in a Fibonacci heap are organized in such a way that the root node with the smallest key is always at the front of the list of trees.
- In a Fibonacci heap, when a new element is inserted, it is added as a singleton tree. When two heaps are merged, the root list of one heap is simply appended to the root list of the other heap. When the extract-min operation is performed, the tree with the minimum root node is removed from the root list and its children are added to the root list.
- One unique feature of a Fibonacci heap is the use of lazy consolidation, which is a technique for improving the efficiency of the merge operation. In lazy consolidation, the merging of trees is postponed until it is necessary, rather than performed immediately. This allows for the merging of trees to be performed more efficiently in batches, rather than one at a time.
In summary, a Fibonacci heap is a highly efficient data structure for implementing priority queues, with fast amortized running times for operations such as insert, merge and extract-min. Its use of lazy consolidation and its multi-tree structure make it a superior alternative to traditional binary and binomial heaps in many applications.
Heaps are mainly used for implementing priority queue. We have discussed the below heaps in previous posts.
In terms of Time Complexity, Fibonacci Heap beats both Binary and Binomial Heap.
Below are amortized time complexities of the Fibonacci Heap.
1) Find Min: ?(1) [Same as Binary but not Binomial since binomial has o(log n)]
2) Delete Min: O(Log n) [?(Log n) in both Binary and Binomial]
3) Insert: ?(1) [?(Log n) in Binary and ?(1) in Binomial]
4) Decrease-Key: ?(1) [?(Log n) in both Binary and Binomial]
5) Merge: ?(1) [?(m Log n) or ?(m+n) in Binary and
?(Log n) in Binomial]
Like Binomial Heap, Fibonacci Heap is a collection of trees with min-heap or max-heap properties. In Fibonacci Heap, trees can have any shape even if all trees can be single nodes (This is unlike Binomial Heap where every tree has to be a Binomial Tree).
Below is an example Fibonacci Heap taken from here.
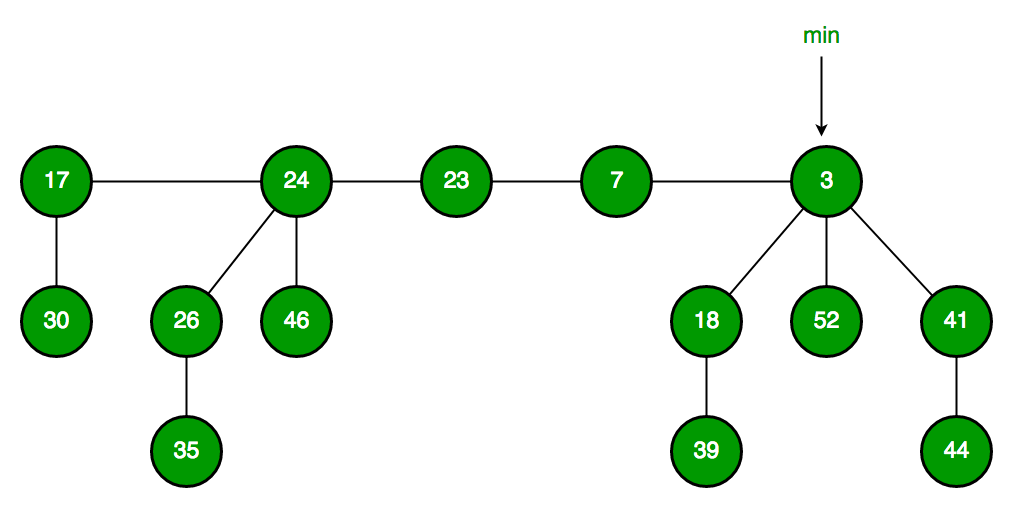
Fibonacci Heap maintains a pointer to the minimum value (which is the root of a tree). All tree roots are connected using a circular doubly linked list, so all of them can be accessed using a single ‘min’ pointer.
The main idea is to execute operations in a “lazy” way. For example merge operation simply links two heaps, insert operation simply adds a new tree with a single node. The operation extract minimum is the most complicated operation. It does delay the work of consolidating trees. This makes delete also complicated as delete first decreases the key to minus infinite, then calls extract minimum.
Below are some interesting facts about Fibonacci Heap
- The reduced time complexity of Decrease-Key has importance in Dijkstra and Prim algorithms. With Binary Heap, the time complexity of these algorithms is O(VLogV + ELogV). If Fibonacci Heap is used, then time complexity is improved to O(VLogV + E)
- Although Fibonacci Heap looks promising time complexity-wise, it has been found slow in practice as hidden constants are high (Source Wiki).
- Fibonacci heaps is mainly called so because Fibonacci numbers are used in the running time analysis. Also, every node in Fibonacci Heap has a degree at most O(log n) and the size of a subtree rooted in a node of degree k is at least Fk+2, where Fk is the kth Fibonacci number.
Advantages of Fibonacci Heap:
- Fast amortized running time: The running time of operations such as insert, extract-min and merge in a Fibonacci heap is O(1) for insert, O(log n) for extract-min and O(1) amortized for merge, making it one of the most efficient data structures for these operations.
- Lazy consolidation: The use of lazy consolidation allows for the merging of trees to be performed more efficiently in batches, rather than one at a time, improving the efficiency of the merge operation.
- Efficient memory usage: Fibonacci heaps have a relatively small constant factor compared to other data structures, making them a more memory-efficient choice in some applications.
Disadvantages of Fibonacci Heap:
- Increased complexity: The structure and operations of a Fibonacci heap are more complex than those of a binary or binomial heap, making it a less intuitive data structure for some users.
- Less well-known: Compared to other data structures, Fibonacci heaps are less well-known and widely used, making it more difficult to find resources and support for implementation and optimization.
References and books:
- “Introduction to Algorithms” by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.
- “Data Structures and Algorithms in Java” by Michael T. Goodrich, Roberto Tamassia and Michael H. Goldwasser.
- “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms” by Michael L. Fredman and Robert E. Tarjan.
- “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms” by J. Ian Munro and Robert E. Tarjan.
We will soon be discussing Fibonacci Heap operations in detail.
Share your thoughts in the comments
Please Login to comment...