Extract bit planes from an Image in Matlab
Last Updated :
28 May, 2017
Image is basically combination of individual pixel (dots) information. When we write that image is of 620 X 480 size, it means that image has 620 pixel in horizontal direction and 480 pixel in vertical direction. So, altogether there is 620 X 480 pixels and each pixels contains some information about image.
Grayscale image are basically those image which we say black and white image. Each pixel of grayscale image has a value lies in between 0 – 255 which decides at which position, the image will be black and at which position, it will be white.
If pixel value is 0, it means that pixel color will be fully black and if pixel value is 255, then that pixel will be fully white and pixel having intermediate value will be having shades of black and white.
We are given a Grayscale Image. Since pixel value of grayscale image lies between 0 -255, so its information is contained using 8 bit. So, we can divide those image into 8 planes (8 Binary Image). Binary image are those images whose pixel value can be either 0 or 1.
So, Our task is to extract each bit planes of original image to make 8 binary image
Let particular pixel of grayscale image has value 212. So, its binary value will be 11010100. So, its 1st bit is 0, 2nd is 0, 3rd is 1, 4rth is 0, 5th is 1, 6th is 0, 7th is 1, 8th is 1. In this manner, we will take these 8 bit of all pixel and will draw 8 binary image. We have to do this to all the pixels and generate new images.
Below is the implementation of above idea in matlab.
clc;
c = imread('cameraman.tif');
cd = double(c);
c1 = mod(cd, 2);
c2 = mod(floor(cd/2), 2);
c3 = mod(floor(cd/4), 2);
c4 = mod(floor(cd/8), 2);
c5 = mod(floor(cd/16), 2);
c6 = mod(floor(cd/32), 2);
c7 = mod(floor(cd/64), 2);
c8 = mod(floor(cd/128), 2);
cc = (2 * (2 * (2 * (2 * (2 * (2 * (2 * c8 + c7) + c6) + c5) + c4) + c3) + c2) + c1);
subplot(2, 5, 1);
imshow(c);
title('Original Image');
subplot(2, 5, 2);
imshow(c1);
title('Bit Plane 1');
subplot(2, 5, 3);
imshow(c2);
title('Bit Plane 2');
subplot(2, 5, 4);
imshow(c3);
title('Bit Plane 3');
subplot(2, 5, 5);
imshow(c4);
title('Bit Plane 4');
subplot(2, 5, 6);
imshow(c5);
title('Bit Plane 5');
subplot(2, 5, 7);
imshow(c6);
title('Bit Plane 6');
subplot(2, 5, 8);
imshow(c7);
title('Bit Plane 7');
subplot(2, 5, 9);
imshow(c8);
title('Bit Plane 8');
subplot(2, 5, 10);
imshow(uint8(cc));
title('Recombined Image');
|
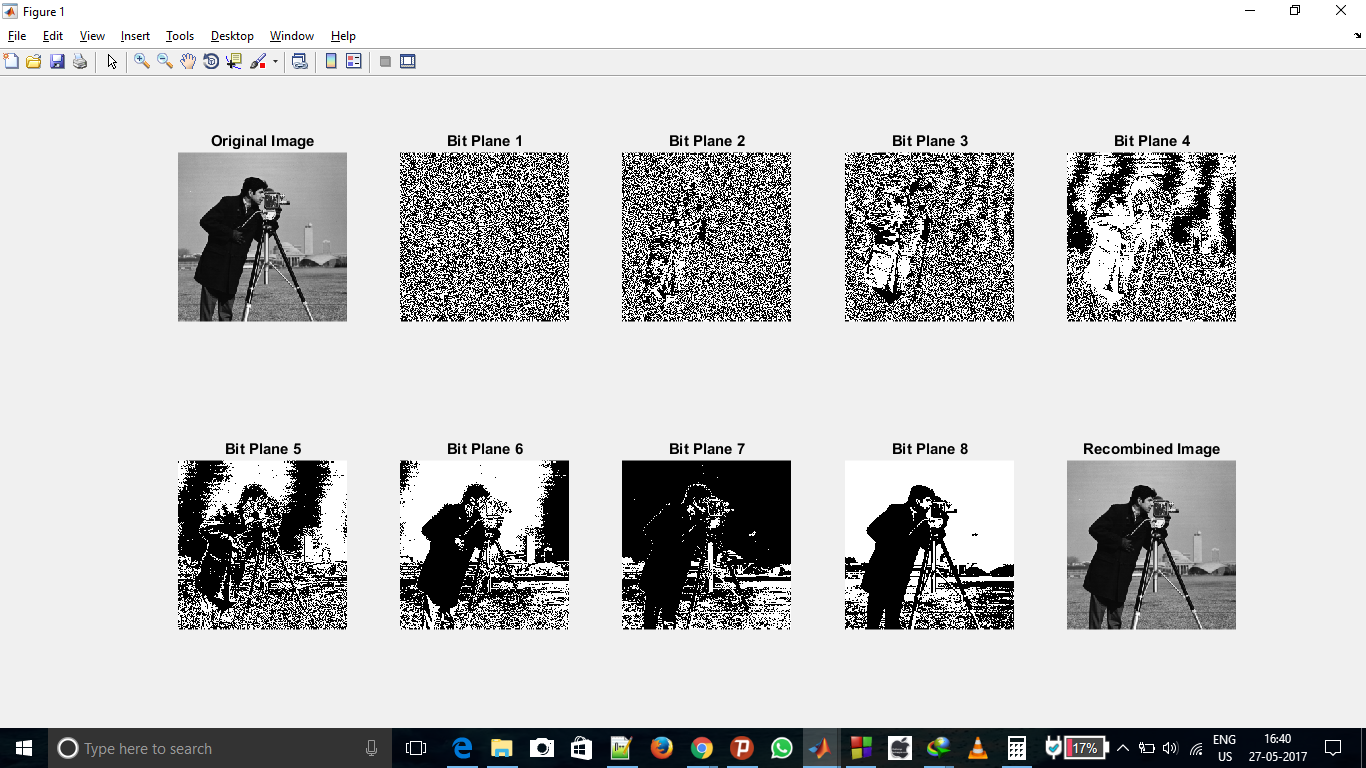
Below is screenshot of obtained output which are 10 images in 10 subplot. 1st one is original image. 2nd image is representation of extracted 1st bit (Least significant bit) image, 3rd one is of 2nd bit and so on. 9th image is extracted 8th bit (Most significant bit) image and 10th image is obtained after recombining of all 8 extracted bit.
Original Image Reference : Here
Share your thoughts in the comments
Please Login to comment...