Distance between a point and a Plane in 3 D

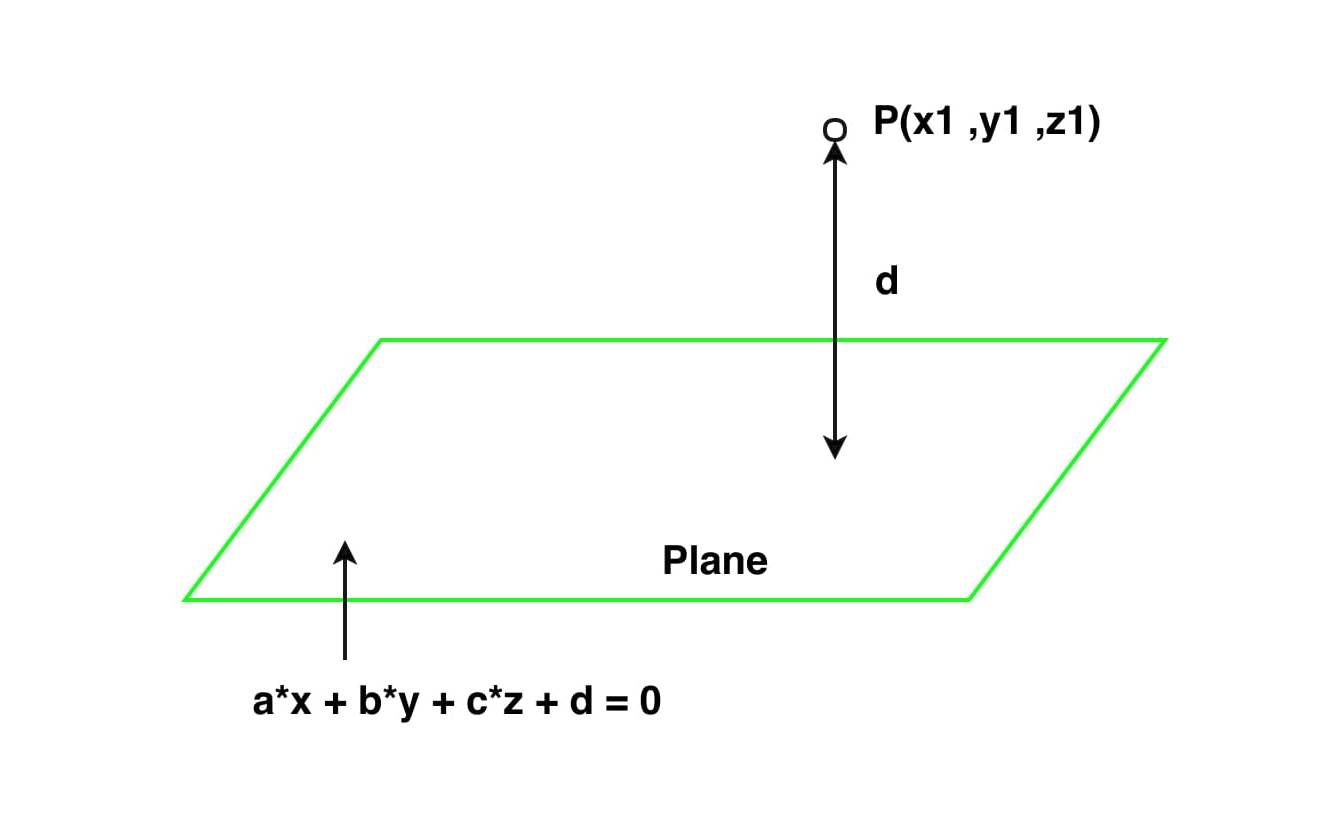
You are given a points (x1, y1, z1) and a plane a * x + b * y + c * z + d = 0. The task is to find the perpendicular(shortest) distance between that point and the given Plane.

Examples :

Input: x1 = 4, y1 = -4, z1 = 3, a = 2, b = -2, c = 5, d = 8 
Output: Perpendicular distance is 6.78902858227
Input: x1 = 2, y1 = 8, z1 = 5, a = 1, b = -2, c = -2, d = -1 
Output: Perpendicular distance is 8.33333333333 

Approach: The perpendicular distance (i.e shortest distance) from a given point to a Plane is the perpendicular distance from that point to the given plane. Let the co-ordinate of the given point be (x1, y1, z1) 
and equation of the plane be given by the equation a * x + b * y + c * z + d = 0, where a, b and c are real constants.
The formula for distance between a point and Plane in 3-D is given by:

Distance = (| a*x1 + b*y1 + c*z1 + d |) / (sqrt( a*a + b*b + c*c))

Below is the implementation of the above formulae: 

C++

// C++ program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
#include<bits/stdc++.h>
#include<math.h>

using namespace std;

// Function to find distance
void shortest_distance(float x1, float y1,
                       float z1, float a,
                       float b, float c,
                       float d)
{
    d = fabs((a * x1 + b * y1 +
              c * z1 + d));
    float e = sqrt(a * a + b *
                   b + c * c);
    cout << "Perpendicular distance is "
         << (d / e);
        return;
}

// Driver Code
int main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;

    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}

// This code is contributed
// by Akanksha Rai(Abby_akku)

C

// C program to find the Perpendicular(shortest)
// distance between a point and a Plane in 3 D.

#include<stdio.h>
#include<math.h>

// Function to find distance
void shortest_distance(float x1, float y1, float z1,
                    float a, float b, float c, float d)
{
    d = fabs((a * x1 + b * y1 + c * z1 + d));
    float e = sqrt(a * a + b * b + c * c);
    printf("Perpendicular distance is %f", d/e);
        return;
}

// Driver Code
int main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;

    // Function call
    shortest_distance(x1, y1, z1, a, b, c, d);
}
// This code is contributed
// by Amber_Saxena.

Java

// Java program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
import java .io.*;

class GFG
{

// Function to find distance
static void shortest_distance(float x1, float y1,
                              float z1, float a,
                              float b, float c,
                              float d)
{
    d = Math.abs((a * x1 + b *
                 y1 + c * z1 + d));
    float e = (float)Math.sqrt(a * a + b *
                               b + c * c);
    System.out.println("Perpendicular distance " +
                                   "is " + d / e);
}

// Driver code
public static void main(String[] args)
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;

    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}
}

// This code is contributed
// by Amber_Saxena.

Python

# Python program to find the Perpendicular(shortest)
# distance between a point and a Plane in 3 D.

import math

# Function to find distance
def shortest_distance(x1, y1, z1, a, b, c, d):

    d = abs((a * x1 + b * y1 + c * z1 + d))
    e = (math.sqrt(a * a + b * b + c * c))
    print("Perpendicular distance is", d/e)


# Driver Code
x1 = 4
y1 = -4
z1 = 3
a = 2
b = -2
c = 5
d = 8

# Function call
shortest_distance(x1, y1, z1, a, b, c, d)

C#

// C# program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.
using System;

class GFG
{

// Function to find distance
static void shortest_distance(float x1, float y1,
                              float z1, float a,
                              float b, float c,
                              float d)
{
    d = Math.Abs((a * x1 + b *
                   y1 + c * z1 + d));
    float e = (float)Math.Sqrt(a * a + b *
                               b + c * c);
    Console.Write("Perpendicular distance " +
                              "is " + d / e);
}

// Driver code
public static void Main()
{
    float x1 = 4;
    float y1 = -4;
    float z1 = 3;
    float a = 2;
    float b = -2;
    float c = 5;
    float d = 8;

    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);
}
}

// This code is contributed
// by ChitraNayal

PHP

<?php
// PHP program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.

// Function to find distance
function shortest_distance($x1, $y1, $z1,
                           $a, $b, $c, $d)
{
    $d = abs(($a * $x1 + $b * $y1 +
              $c * $z1 + $d));
    $e = sqrt($a * $a + $b *
              $b + $c * $c);
    echo "Perpendicular distance is ". $d / $e;
}

// Driver Code
$x1 = 4;
$y1 = -4;
$z1 = 3;
$a = 2;
$b = -2;
$c = 5;
$d = 8;

// function call
shortest_distance($x1, $y1, $z1,
                  $a, $b, $c, $d);

// This code is contributed
// by Amber_Saxena.
?>

Javascript

<script>


// Javascript program to find the
// Perpendicular(shortest)
// distance between a point
// and a Plane in 3 D.

// Function to find distance
function shortest_distance( x1,  y1, z1,  a,
                        b,  c, d)
{
    d = Math.abs((a * x1 + b * y1 +
              c * z1 + d));
    let e = Math.sqrt(a * a + b *
                   b + c * c);
    document.write("Perpendicular distance is "
         + (d / e));
        return;
}

    // driver code
    let x1 = 4;
    let y1 = -4;
    let z1 = 3;
    let a = 2;
    let b = -2;
    let c = 5;
    let d = 8;

    // Function call
    shortest_distance(x1, y1, z1,
                      a, b, c, d);

 // This code is contributed by jana_sayantan.
</script>

Output:

Perpendicular distance is 6.78902858227

Time complexity: O(log(a²+b²+c²)) as inbuilt sqrt function is being used
Auxiliary space: O(1)