Find the foot of perpendicular of a point in a 3 D plane

Given a point (x1, y1, z1) in 3-D and coefficients of the equation of plane, we have to find the foot of perpendicular of a point in a 3 D plane.
Examples:

Input: a = 1, b = -2, c = 0, d = 0, x = -1, y = 3, z = 4 
Output: x2 = 0.4 y2 = 0.2 z2 = 4.0

Input: a = 2, b = -1, c = 1, d = 3, x = 1, y = 3, z = 4 
Output: x2 = -1.0 y2 = 4.0 z2 = 3.0

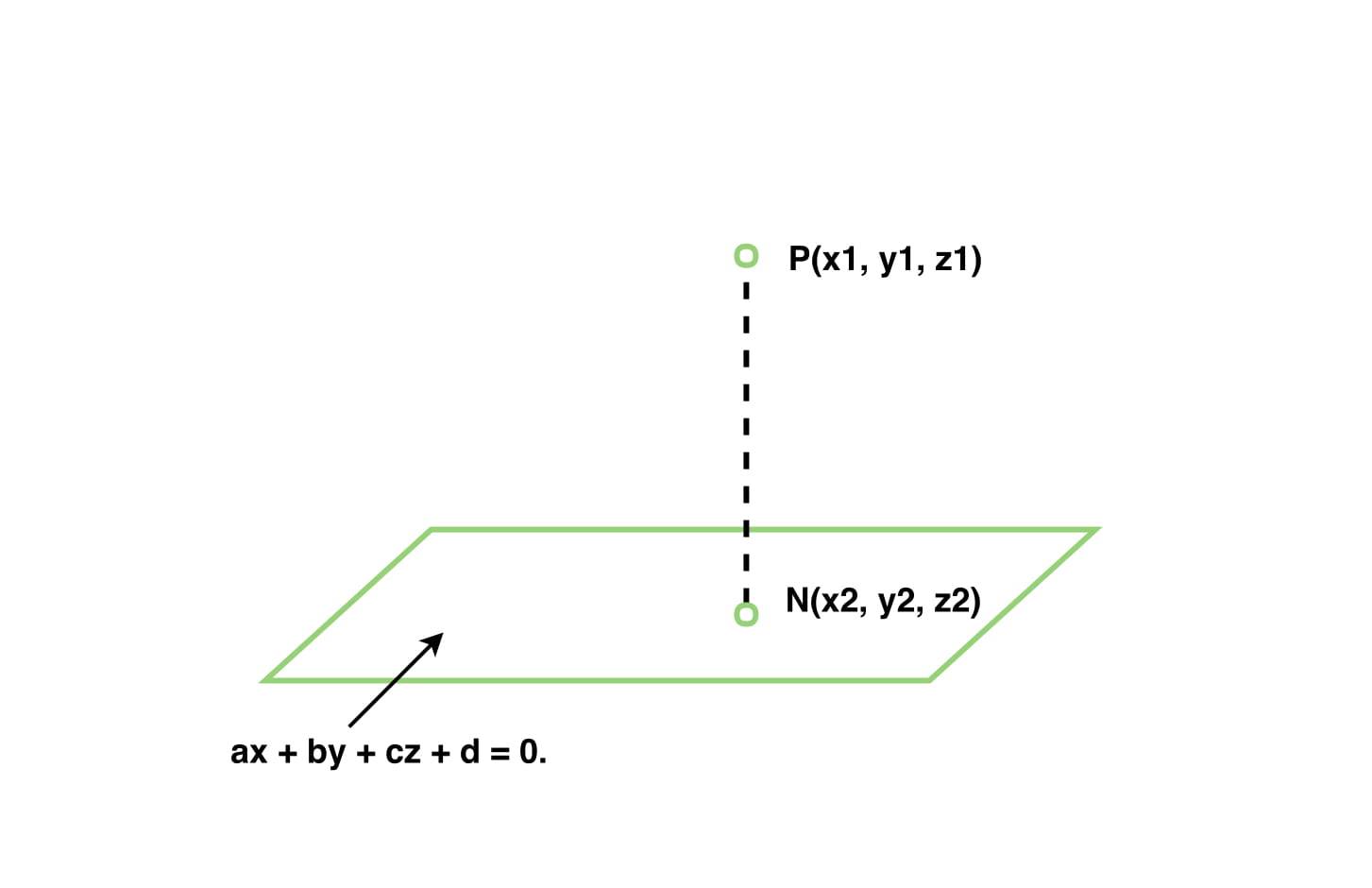
Approach: Equation of plane is given as ax + by + cz + d = 0. Therefore, the direction ratios of the normal to the plane are (a, b, c). Let N be the foot of perpendicular from given point to the given plane so, line PN has directed ratios (a, b, c) and it passes through P(x1, y1, z1). 
The equation of line PN will be as:-

(x – x1) / a = (y – y1) / b = (z – z1) / c = k

Hence any point on line PN can be written as:-

x = a * k + x1 
y = b * k + y1 
z = c * k + z1

since N lies in both line and plane so will satisfy(ax + by + cz + d = 0).

=>a * (a * k + x1) + b * (b * k + y1) + c * (c * k + z1) + d = 0. 
=>a * a * k + a * x1 + b * b * k + b * y1 + c * c * k + c * z1 + d = 0. 
=>(a * a + b * b + c * c)k = -a * x1 – b * y1 – c * z1 – d. 
=>k = (-a * x1 – b * y1 – c * z1 – d) / (a * a + b * b + c * c).

Now, the coordinates of Point N in terms of k will be:- 

x2 = a * k + x1 
y2 = b * k + y1 
z2 = c * k + z1

Below is the implementation of the above: 

C++

// C++ program to find
// foot of perpendicular
// of a point in a 3 D plane.
#include <bits/stdc++.h>
#include <iomanip>
#include <iostream>
#include <math.h>
using namespace std;

// Function to find foot of perpendicular
void foot(float a, float b,
          float c, float d,
          float x1, float y1,
          float z1)
{
    float k = (-a * x1 - b * y1 - c * z1 - d) / (float)(a * a + b * b + c * c);
    float x2 = a * k + x1;
    float y2 = b * k + y1;
    float z2 = c * k + z1;

    std::cout << std::fixed;
    std::cout << std::setprecision(1);
    cout << " x2 = " << x2;
    cout << " y2 = " << y2;
    cout << " z2 = " << z2;
}

// Driver Code
int main()
{
    float a = 1;
    float b = -2;
    float c = 0;
    float d = 0;
    float x1 = -1;
    float y1 = 3;
    float z1 = 4;

    // function call
    foot(a, b, c, d, x1, y1, z1);
    return 0;
}
// This code is contributed  by Amber_Saxena.

Java

// Java program to find
// foot of perpendicular
// of a point in a 3 D plane.
import java.util.*;
import java.text.*;

class solution
{

// Function to find foot of perpendicular
static void foot(float a, float b,
        float c, float d,
        float x1, float y1,
        float z1)
{
    float k = (-a * x1 - b * y1 - c * z1 - d) / (float)(a * a + b * b + c * c);
    float x2 = a * k + x1;
    float y2 = b * k + y1;
    float z2 = c * k + z1;
    DecimalFormat form = new DecimalFormat("0.0");
    System.out.print(" x2 = " +form.format(x2));
    System.out.print(" y2 = " +form.format(y2));
    System.out.print( " z2 = " +form.format(z2));
}

// Driver Code
public static void main(String arr[])
{
    float a = 1;
    float b = -2;
    float c = 0;
    float d = 0;
    float x1 = -1;
    float y1 = 3;
    float z1 = 4;

    // function call
    foot(a, b, c, d, x1, y1, z1);

}
}

Python3

# Python3 program to find
# foot of perpendicular
# of a point in a 3 D plane.

# Function to find foot of perpendicular
def foot(a, b, c, d, x1, y1, z1) :

    k = (-a * x1 - b * y1 - c * z1 - d) / (a * a + b * b + c * c);
    x2 = a * k + x1;
    y2 = b * k + y1;
    z2 = c * k + z1;

    print("x2 =",round(x2,1))
    print("y2 =",round(y2,1))
    print("z2 =",round(z2,1))


# Driver Code
if __name__ == "__main__" :

    a = 1
    b = -2
    c = 0
    d = 0
    x1 = -1
    y1 = 3
    z1 = 4

    # function call
    foot(a, b, c, d, x1, y1, z1)

# This code is contributed by Ryuga

C#

// C# program to find
// foot of perpendicular
// of a point in a 3 D plane.
using System;
using System.Globalization;

class GFG
{

// Function to find foot of perpendicular
static void foot(float a, float b,
        float c, float d,
        float x1, float y1,
        float z1)
{
    float k = (-a * x1 - b * y1 - c * z1 - d) /
                (float)(a * a + b * b + c * c);
    float x2 = a * k + x1;
    float y2 = b * k + y1;
    float z2 = c * k + z1;
    NumberFormatInfo form = new NumberFormatInfo();
    form.NumberDecimalSeparator = ".";
    Console.Write(" x2 = " + x2.ToString(form));
    Console.Write(" y2 = " + y2.ToString(form));
    Console.Write( " z2 = " + z2.ToString(form));
}

// Driver Code
public static void Main(String []arr)
{
    float a = 1;
    float b = -2;
    float c = 0;
    float d = 0;
    float x1 = -1;
    float y1 = 3;
    float z1 = 4;

    // function call
    foot(a, b, c, d, x1, y1, z1);
}
}

// This code contributed by Rajput-Ji

PHP

<?php
// PHP program to find foot of perpendicular
// of a point in a 3 D plane.

// Function to find foot of perpendicular
function foot($a, $b, $c, $d, $x1, $y1, $z1)
{
    $k = (-$a * $x1 - $b * $y1 - $c * $z1 - $d) /
                  ($a * $a + $b * $b + $c * $c);
    $x2 = $a * $k + $x1;
    $y2 = $b * $k + $y1;
    $z2 = $c * $k + $z1;

    echo "x2 = " . round($x2, 1);
    echo " y2 = " . round($y2, 1);
    echo " z2 = " . round($z2, 1);
}

// Driver Code
$a = 1; $b = -2; $c = 0; $d = 0;
$x1 = -1; $y1 = 3; $z1 = 4;

// function call
foot($a, $b, $c, $d, $x1, $y1, $z1);

// This code is contributed by ita_c
?>

Javascript

<script>
      // JavaScript program to find
      // foot of perpendicular
      // of a point in a 3 D plane.

      // Function to find foot of perpendicular
      function foot(a, b, c, d, x1, y1, z1) {
        var k = (-a * x1 - b * y1 - c * z1 - d) / (a * a + b * b + c * c);
        var x2 = a * k + x1;
        var y2 = b * k + y1;
        var z2 = c * k + z1;

        document.write("x2 =" + x2.toFixed(1) + " ");
        document.write("y2 =" + y2.toFixed(1) + " ");
        document.write("z2 =" + z2.toFixed(1) + " ");
      }

      // Driver Code

      var a = 1;
      var b = -2;
      var c = 0;
      var d = 0;
      var x1 = -1;
      var y1 = 3;
      var z1 = 4;

      // function call
      foot(a, b, c, d, x1, y1, z1);
    </script>

Output:

x2 = 0.4 y2 = 0.2 z2 = 4.0

Time complexity: O(1)
Auxiliary space: O(1)