Find foot of perpendicular from a point in 2 D plane to a Line
Last Updated :
09 Jun, 2022
Given a point P in 2-D plane and equation of a line, the task is to find the foot of the perpendicular from P to the line.
Note: Equation of line is in form ax+by+c=0.
Examples:
Input : P=(1, 0), a = -1, b = 1, c = 0
Output : Q = (0.5, 0.5)
The foot of perpendicular from point (1, 0)
to line -x + y = 0 is (0.5, 0.5)
Input : P=(3, 3), a = 0, b = 1, c = -2
Output : Q = (3, 2)
The foot of perpendicular from point (3, 3)
to line y-2 = 0 is (3, 2)
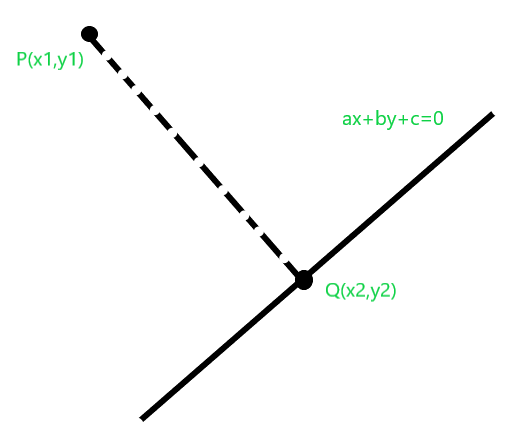
Since equation of the line is given to be of the form ax + by + c = 0. Equation of line passing through P and is perpendicular to line. Therefore equation of line passing through P and Q becomes ay – bx + d = 0. Also, P passes through line passing through P and Q, so we put coordinate of P in the above equation:
ay1 - bx1 + d = 0
or, d = bx1 - ay1
Also, Q is the intersection of the given line and the line passing through P and Q. So we can find the solution of:
ax + by + c = 0
and,
ay - bx + (bx1-ay1) = 0
Since a, b, c, d all are known we can find x and y here as:
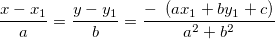
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
pair<double, double> findFoot(double a, double b, double c,
double x1, double y1)
{
double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
double x = temp * a + x1;
double y = temp * b + y1;
return make_pair(x, y);
}
int main()
{
double a = 0.0;
double b = 1.0;
double c = -2;
double x1 = 3.0;
double y1 = 3.0;
pair<double, double> foot = findFoot(a, b, c, x1, y1);
cout << foot.first << " " << foot.second;
return 0;
}
|
Java
import javafx.util.Pair;
class GFG
{
static Pair<Double, Double> findFoot(double a, double b, double c,
double x1, double y1)
{
double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
double x = temp * a + x1;
double y = temp * b + y1;
return new Pair(x, y);
}
public static void main(String[] args)
{
double a = 0.0;
double b = 1.0;
double c = -2;
double x1 = 3.0;
double y1 = 3.0;
Pair<Double, Double> foot = findFoot(a, b, c, x1, y1);
System.out.println(foot.getKey() + " " + foot.getValue());
}
}
|
Python3
def findFoot(a, b, c, x1, y1):
temp = (-1 * (a * x1 + b * y1 + c) //
(a * a + b * b))
x = temp * a + x1
y = temp * b + y1
return (x, y)
if __name__ == "__main__":
a, b, c = 0.0, 1.0, -2
x1, y1 = 3.0, 3.0
foot = findFoot(a, b, c, x1, y1)
print(int(foot[0]), int(foot[1]))
|
C#
using System;
class GFG
{
public class Pair
{
public double first,second;
public Pair(double a,double b)
{
first = a;
second = b;
}
}
static Pair findFoot(double a, double b, double c,
double x1, double y1)
{
double temp = -1 * (a * x1 + b * y1 + c) / (a * a + b * b);
double x = temp * a + x1;
double y = temp * b + y1;
return new Pair(x, y);
}
public static void Main(String []args)
{
double a = 0.0;
double b = 1.0;
double c = -2;
double x1 = 3.0;
double y1 = 3.0;
Pair foot = findFoot(a, b, c, x1, y1);
Console.WriteLine(foot.first + " " + foot.second);
}
}
|
PHP
<?php
function findFoot($a, $b, $c, $x1, $y1)
{
$temp = floor((-1 * ($a * $x1 + $b * $y1 + $c) /
($a * $a + $b * $b)));
$x = $temp * $a + $x1;
$y = $temp * $b + $y1;
return array($x, $y);
}
$a = 0.0;
$b = 1.0 ;
$c = -2 ;
$x1 = 3.0 ;
$y1 = 3.0 ;
$foot = findFoot($a, $b, $c, $x1, $y1);
echo floor($foot[0]), " ", floor($foot[1]);
?>
|
Javascript
<script>
function findFoot(a, b, c, x1, y1) {
var temp = (-1 * (a * x1 + b * y1 + c)) / (a * a + b * b);
var x = temp * a + x1;
var y = temp * b + y1;
return [x, y];
}
var a = 0.0;
var b = 1.0;
var c = -2;
var x1 = 3.0;
var y1 = 3.0;
var foot = findFoot(a, b, c, x1, y1);
document.write(parseInt(foot[0]) + " " + parseInt(foot[1]));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...