Detect Cycle in a Directed Graph using BFS
Last Updated :
28 Jul, 2022
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains two cycles 0->1->2->3->0 and 2->4->2, so your function must return true.
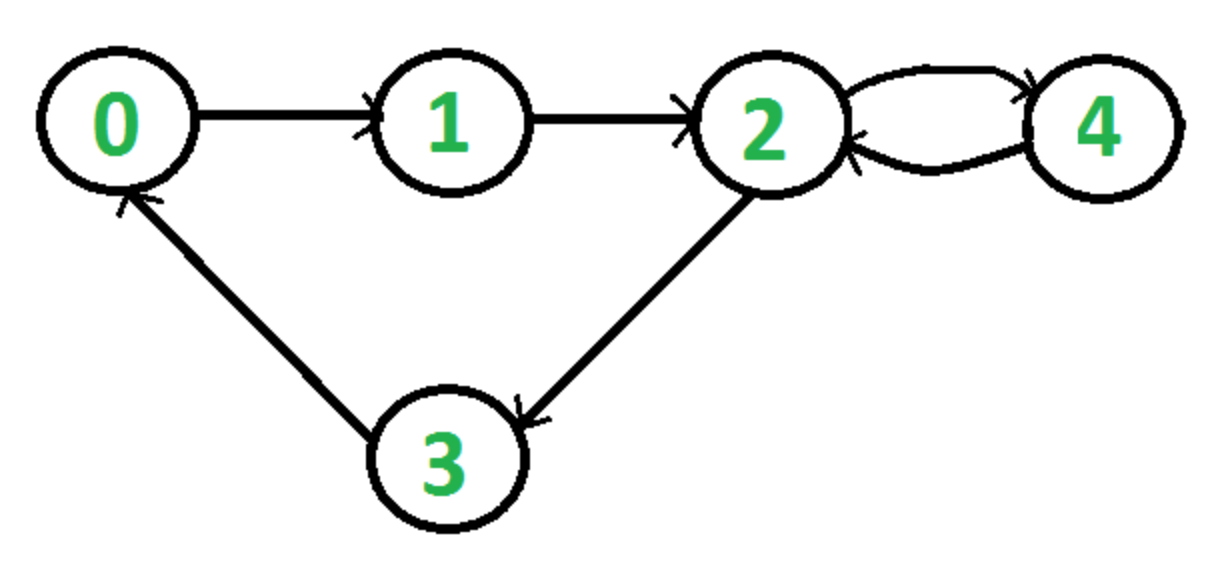
We have discussed a DFS based solution to detect cycle in a directed graph. In this post, BFS based solution is discussed.
The idea is to simply use Kahn’s algorithm for Topological Sorting
Steps involved in detecting cycle in a directed graph using BFS.
Step-1: Compute in-degree (number of incoming edges) for each of the vertex present in the graph and initialize the count of visited nodes as 0.
Step-2: Pick all the vertices with in-degree as 0 and add them into a queue (Enqueue operation)
Step-3: Remove a vertex from the queue (Dequeue operation) and then.
- Increment count of visited nodes by 1.
- Decrease in-degree by 1 for all its neighboring nodes.
- If in-degree of a neighboring nodes is reduced to zero, then add it to the queue.
Step 4: Repeat Step 3 until the queue is empty.
Step 5: If count of visited nodes is not equal to the number of nodes in the graph has cycle, otherwise not.
How to find in-degree of each node?
There are 2 ways to calculate in-degree of every vertex:
Take an in-degree array which will keep track of
1) Traverse the array of edges and simply increase the counter of the destination node by 1.
for each node in Nodes
indegree[node] = 0;
for each edge(src,dest) in Edges
indegree[dest]++
Time Complexity: O(V+E)
2) Traverse the list for every node and then increment the in-degree of all the nodes connected to it by 1.
for each node in Nodes
If (list[node].size()!=0) then
for each dest in list
indegree[dest]++;
Time Complexity: The outer for loop will be executed V number of times and the inner for loop will be executed E number of times, Thus overall time complexity is O(V+E).
The overall time complexity of the algorithm is O(V+E)
C++
#include <bits/stdc++.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
public:
Graph(int V);
void addEdge(int u, int v);
bool isCycle();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int u, int v)
{
adj[u].push_back(v);
}
bool Graph::isCycle()
{
vector<int> in_degree(V, 0);
for (int u = 0; u < V; u++) {
for (auto v : adj[u])
in_degree[v]++;
}
queue<int> q;
for (int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.push(i);
int cnt = 1;
vector<int> top_order;
while (!q.empty()) {
int u = q.front();
q.pop();
top_order.push_back(u);
list<int>::iterator itr;
for (itr = adj[u].begin(); itr != adj[u].end(); itr++)
if (--in_degree[*itr] == 0)
{
q.push(*itr);
cnt++;
}
}
if (cnt != V)
return true;
else
return false;
}
int main()
{
Graph g(6);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(3, 4);
g.addEdge(4, 5);
if (g.isCycle())
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG
{
static class Graph
{
int V;
Vector<Integer>[] adj;
@SuppressWarnings("unchecked")
Graph(int V)
{
this.V = V;
this.adj = new Vector[V];
for (int i = 0; i < V; i++)
adj[i] = new Vector<>();
}
void addEdge(int u, int v)
{
adj[u].add(v);
}
boolean isCycle()
{
int[] in_degree = new int[this.V];
Arrays.fill(in_degree, 0);
for (int u = 0; u < V; u++)
{
for (int v : adj[u])
in_degree[v]++;
}
Queue<Integer> q = new LinkedList<Integer>();
for (int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.add(i);
int cnt = 0;
Vector<Integer> top_order = new Vector<>();
while (!q.isEmpty())
{
int u = q.poll();
top_order.add(u);
for (int itr : adj[u])
if (--in_degree[itr] == 0)
q.add(itr);
cnt++;
}
if (cnt != this.V)
return true;
else
return false;
}
}
public static void main(String[] args)
{
Graph g = new Graph(6);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(3, 4);
g.addEdge(4, 5);
if (g.isCycle())
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
import math
import sys
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.graph=defaultdict(list)
self.V=vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def isCycleExist(n,graph):
in_degree=[0]*n
for i in range(n):
for j in graph[i]:
in_degree[j]+=1
queue=[]
for i in range(len(in_degree)):
if in_degree[i]==0:
queue.append(i)
cnt=0
while(queue):
nu=queue.pop(0)
for v in graph[nu]:
in_degree[v]-=1
if in_degree[v]==0:
queue.append(v)
cnt+=1
if cnt==n:
return False
else:
return True
if __name__=='__main__':
g=Graph(6)
g.addEdge(0,1)
g.addEdge(1,2)
g.addEdge(2,0)
g.addEdge(3,4)
g.addEdge(4,5)
if isCycleExist(g.V,g.graph):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG{
public class Graph
{
public int V;
public List<int>[] adj;
public Graph(int V)
{
this.V = V;
this.adj = new List<int>[V];
for (int i = 0; i < V; i++)
adj[i] = new List<int>();
}
public void addEdge(int u, int v)
{
adj[u].Add(v);
}
public bool isCycle()
{
int[] in_degree = new int[this.V];
for(int u = 0; u < V; u++)
{
foreach(int v in adj[u])
in_degree[v]++;
}
Queue<int> q = new Queue<int>();
for(int i = 0; i < V; i++)
if (in_degree[i] == 0)
q.Enqueue(i);
int cnt = 0;
List<int> top_order = new List<int>();
while (q.Count != 0)
{
int u = q.Peek();
q.Dequeue();
top_order.Add(u);
foreach(int itr in adj[u])
if (--in_degree[itr] == 0)
q.Enqueue(itr);
cnt++;
}
if (cnt != this.V)
return true;
else
return false;
}
}
public static void Main(String[] args)
{
Graph g = new Graph(6);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(3, 4);
g.addEdge(4, 5);
if (g.isCycle())
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
var V = 0;
var adj ;
function initialize(v)
{
V = v;
adj = Array.from(Array(V), ()=>Array(V));
}
function addEdge(u, v)
{
adj[u].push(v);
}
function isCycle()
{
var in_degree = Array(V).fill(0);
for(var u = 0; u < V; u++)
{
for(var v of adj[u])
in_degree[v]++;
}
var q = [];
for(var i = 0; i < V; i++)
if (in_degree[i] == 0)
q.push(i);
var cnt = 0;
var top_order = [];
while (q.length != 0)
{
var u = q[0];
q.shift();
top_order.push(u);
for(var itr of adj[u])
if (--in_degree[itr] == 0)
q.push(itr);
cnt++;
}
if (cnt != V)
return true;
else
return false;
}
initialize(6)
addEdge(0, 1);
addEdge(1, 2);
addEdge(2, 0);
addEdge(3, 4);
addEdge(4, 5);
if (isCycle())
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(V+E)
Auxiliary Space: O(V)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...