Congruent Angles

Congruent angles are angles that have equal measure. Thus, all the angles in the geometry that have sam measure are called congruent angles.

In this article, we will understand the meaning of congruent angles, their properties, the congruent angles theorem, the vertical angles theorem, the corresponding angles theorem, and the alternate angles theorem.

What are Congruent Angles?

Congruent angles are angles that have the same measure. In simpler terms, if two angles are equal in measure, they are called congruent angles.

Congruent angles are represented using the”≅” symbol. For example, if we want to say that angle A is congruent to angle X, we write it as ∠A ≅ ∠X.

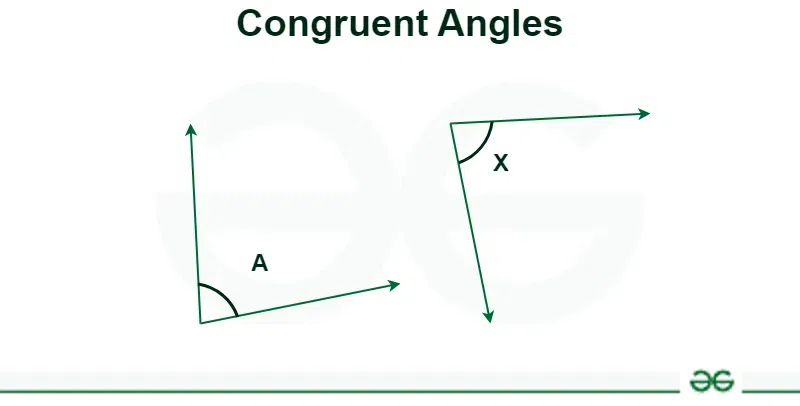
Congruent Angles

So, when two angles have the same measure or rotation, no matter where they are, we call them congruent angles.

Congruent Angles Symbol

The symbol used to represent congruent angles is “≅”. This symbol indicates that two angles have the same measure and are therefore congruent.

Examples of Congruent Angles

Examples of congruent angles are listed below:

• Corresponding Congruent Angles
• Alternate Angles
• Vertical Angles

Congruent Angles Theorem

Several theorems rely on congruent angles to determine whether two angles are congruent or not. These theorems include:

• Vertical Angles Theorem: This theorem states that vertical angles, formed by the intersection of two lines, are congruent.
• Corresponding Angles Theorem: When a transversal intersects two parallel lines, corresponding angles are congruent.
• Alternate Angles Theorem: Alternate interior and alternate exterior angles, formed when a transversal intersects two parallel lines, are congruent.
• Congruent Supplements Theorem: If two angles are supplements of congruent angles (i.e., they add up to 180 degrees), then the two angles are congruent.
• Congruent Complements Theorem: If two angles are complements of congruent angles (i.e., they add up to 90 degrees), then the two angles are congruent.

Vertical Angles Theorem

Vertical Angles Theorem states that when two lines intersect, the angles formed across from each other (called vertical angles) are congruent. In other words, if two lines cross at a point, the angles opposite each other are equal.

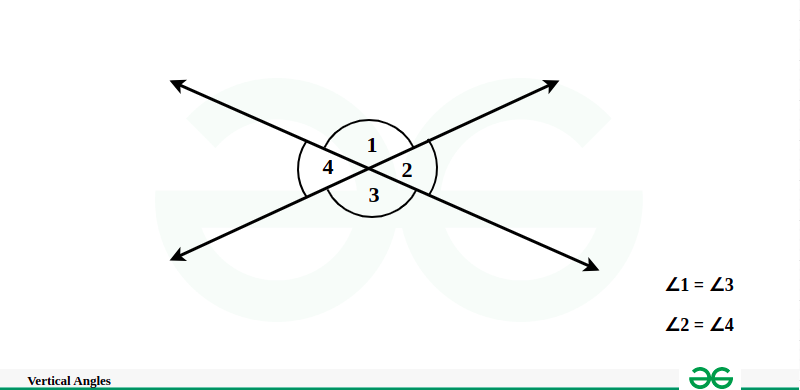
Proof of Vertical Angle Theorem

The proof of vertical angle theorem is mentioned below:

Let’s consider two intersecting lines, line AB and line CD, as shown below:

When lines AB and CD intersect, they form four angles: ∠1, ∠2, ∠3, and ∠4.

Now, let’s examine the relationships between these angles:

• ∠1 and ∠3 are opposite each other and are formed by intersecting lines AB and CD.
• ∠2 and ∠4 are opposite each other and are also formed by intersecting lines AB and CD.
• ∠1 and ∠2 are adjacent angles.
• ∠3 and ∠4 are adjacent angles.

Given that lines AB and CD are straight lines, they form a straight angle. This means that ∠1 and ∠2 together form a straight angle, and ∠3 and ∠4 together form a straight angle.

Since a straight angle measures 180 degrees, we can write:

∠1 + ∠2 = 180° …..(i)

∠3 + ∠4 = 180° …..(ii)

Now, let’s rearrange equation (i) to solve for ∠1:

∠1 = 180° – ∠2 …..(iii)

Similarly, rearrange equation (ii) to solve for ∠3:

∠3 = 180° – ∠4 …..(iv)

Now, we can see that equations (iii) and (iv) show that ∠1 and ∠3 are equal in measure:

∠1 = ∠3

Hence, vertical angles ∠1 and ∠3 are equal

Corresponding Angles Theorem

Corresponding Angles Theorem states that when a transversal intersects two parallel lines, the corresponding angles formed on the same side of the transversal are congruent.

Proof of Corresponding Angles Theorem

Consider two parallel lines, labelled as line m and line n, intersected by a transversal line t.

• Let’s denote the angles formed by the intersection of the transversal t with lines m and n as follows:
  • ∠1 and ∠2 on one side of the transversal, both intersecting line m.
  • ∠3 and ∠4 on the other side of the transversal, both intersecting line n.
• Because lines m and n are parallel, corresponding angles formed by the intersection of the transversal with these lines are equal.
• Now, focus on angles 1 and 3. Since they are corresponding angles (they occupy the same relative position with respect to the transversal and the parallel lines), they are congruent.
• Similarly, angles 2 and 4 are corresponding angles and are also congruent.
• Thus, we have shown that when a transversal intersects two parallel lines, the corresponding angles formed on the same side of the transversal are congruent.

Alternate Angles Theorem

Alternate Angles Theorem, also known as the Alternate Interior Angles Theorem, states that when a transversal intersects two parallel lines, the alternate interior angles formed are congruent.

Proof of Alternate Angles Theorem

The proof of alternate angles theorem is discussed below:

To prove this theorem, let’s consider two parallel lines, ℓ1 and ℓ2​, intersected by a transversal line, t, as shown below:

∠3 and ∠5 be alternate interior angles formed by the transversal t intersecting lines ℓ1 and ℓ2​.

Now, from Corresponding Angle Theorem,

∠1 = ∠5 (Corresponding Angles)…..(i)

Now, from Vertical Angle Theorem,

∠1 = ∠3 (Vertical Angles)…..(ii)

Hence, from equations (i) and (ii)

∠3 = ∠5

Hence, alternate angles ∠3 and ∠5 are corresponding to each other.

Congruent Supplements Theorem

Congruent Supplements Theorem states that if two angles are supplements of congruent angles, then the two angles are congruent. In simpler terms, if two angles add up to 180 degrees and those angles they add up to are congruent, then the two angles themselves are congruent.

Proof of Congruent Supplement Theorem

The proof of congruent supplement theorem is explained below:

Let’s consider two angles, angle A and angle B, which are supplements of congruent angles angle X and angle Y, respectively.

Given: ∠A and ∠B are supplements, and ∠X ≅ ∠Y (congruent angles).

• We know that the sum of the measures of supplementary angles is 180 degrees.
• So, we have: ∠A + ∠X = 180° and ∠B + ∠Y = 180°.
• Since ∠X ≅ ∠Y, we can substitute ∠X for ∠Y in the equation: ∠B + ∠X = 180°.
• Now, from step 4, we have: ∠A + ∠X = 180° and ∠B + ∠X = 180°.
• Subtracting ∠X from both sides of the equations, we get: ∠A = ∠B.
• Thus, we have proven that if ∠A and ∠B are supplements of congruent angles ∠X and ∠Y, respectively, then ∠A ≅ ∠B.

Congruent Complements Theorem

Congruent Complements Theorem states that if two angles are complements of congruent angles, meaning they add up to 90 degrees individually, then the two angles themselves are congruent.

Given:

• ∠A and ∠B are complements
• ∠A is congruent to ∠C
• ∠B is congruent to ∠D

To prove:

• ∠A is congruent to ∠C
• ∠B is congruent to ∠D

Proof of Congruent Complement Theorem

• ∠A + ∠B = 90∘ (Given: ∠A and ∠B are complements)
• Since ∠A is congruent to ∠C, we can substitute ∠C for ∠A: ∠C + ∠B = 90∘
• Similarly, since ∠B is congruent to ∠D, we can substitute ∠D for ∠B: ∠C + ∠D = 90∘
• Since the sum of angles ∠C and ∠D is also 90 degrees, and by the definition of complementary angles, angles ∠C and ∠D are also complements of each other.
• Therefore, by definition, angles ∠C and ∠D are congruent.
• Thus, ∠A is congruent to ∠C and ∠B is congruent to ∠D, as required.

How to Find Congruent Angles

We can find congruent angles using the following steps

Step 1: Look for pairs of angles in the given geometric configuration, such as triangles, parallel lines, or intersecting lines.

Step 2: Familiarize yourself with angle relationships. Know the theorems related to congruent angles, like the Vertical Angles Theorem, Corresponding Angles Theorem, Alternate Angles Theorem, and others.

Step 3: If you have parallel lines and a transversal, use the properties of corresponding angles, alternate angles, and interior angles to identify congruent angles.

Step 4: If the problem involves complementary or supplementary angles, understand that if two angles are complements or supplements of congruent angles, then they are congruent themselves.

Step 5: If you know that angle A is congruent to angle B, and angle B is congruent to angle C, then, by the transitive property, angle A must be congruent to angle C.

Step 6: Utilize any given information about congruent angles explicitly mentioned in the problem. If the problem provides that certain angles are congruent, make use of that information.

Step 7: If two angles are complementary and each is congruent to another angle, then the two angles themselves are congruent.

Step 8: If you have algebraic expressions representing angle measures, set them equal to each other and solve the equation to find the values that make the angles congruent.

Step 9: Double-check your findings by applying relevant congruence theorems to ensure the angles satisfy the specified conditions.

Step 10: When expressing your answer, use the symbol “≅” to denote congruence. For example, if angle A is congruent to angle B, write it as ∠A ≅ ∠B.

Constructing Congruent Angles

We can construct congruent angles in two ways by comparing the measurement to a given angle and constructing two angle at same time. Hence, we will learn the construction steps for two methods:

Construction of a Congruent Angle to the Given Angle

The steps to construct a congruent angle to the given angle is mentioned below:

Step 1: Draw two horizontal lines of any suitable length using a pencil and a ruler.

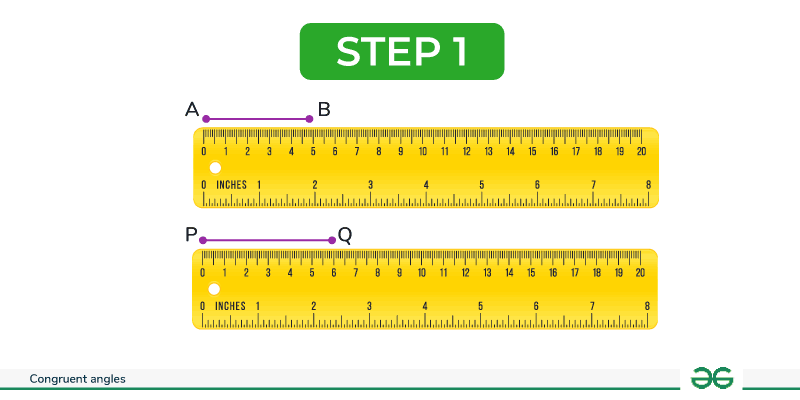
Step 2: Take an arc on your compass, shorter than the length of the lines drawn in the first step. Place the compass tip at the endpoint of one line. Draw the arc while keeping the lines AB and PQ as the base without changing the width of the compass.

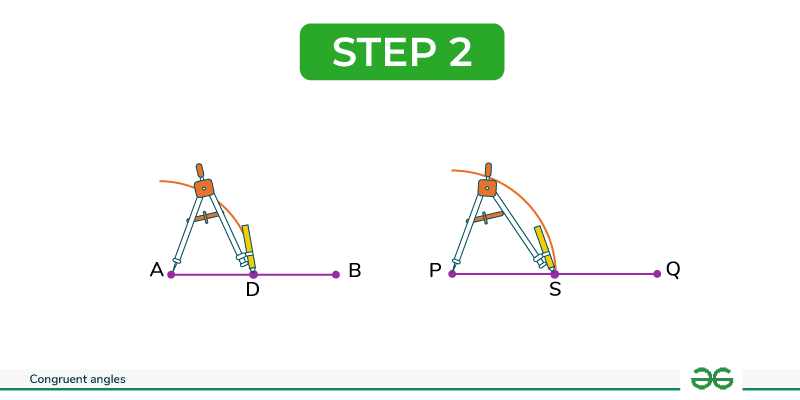
Step 3: With the compass tip at point D, extend the compass legs to draw an arc of any suitable length. Draw the arc and repeat the process with the same arc, placing the compass tip at point S.

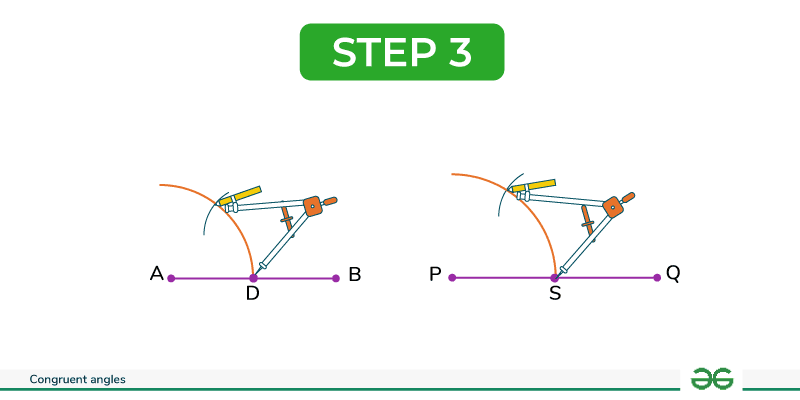
Step 4: Draw lines to connect points A and C, and points P and R.

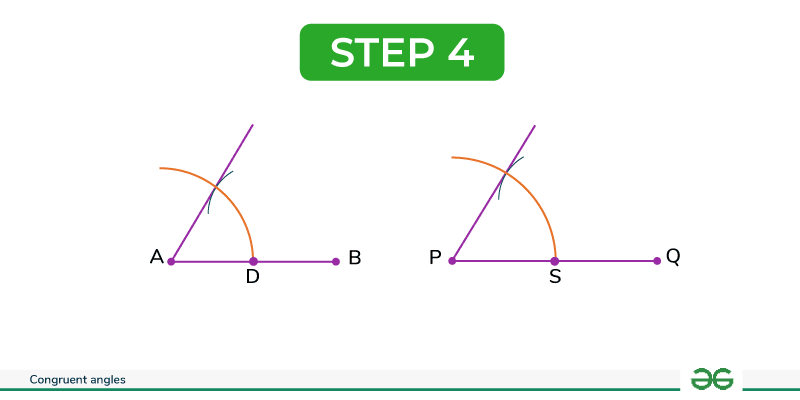
This construction yields two congruent angles in geometry: ∠CAB and ∠RPQ.

Construction of Two Congruent Angles

To construct two congruent angles, you can follow these steps using a straightedge and a compass:

Step 1: Draw a horizontal line of any suitable length and label it AB.

Step 2: Place the compass tip at point B in the given angle. Draw an arc with BC as the base and label the point of intersection with the line YZ as D.

Step 3: Using the same compass width, draw an arc with the compass tip at point Y, labeling the intersection point with line YZ as O.

Step 4: Place the compass tip at point D and measure the arc from D to the intersection point of the arc with segment AB.

Step 5: Using the same arc, place the compass tip at point O and mark a cut on the arc drawn in step 3, labeling this point as X.

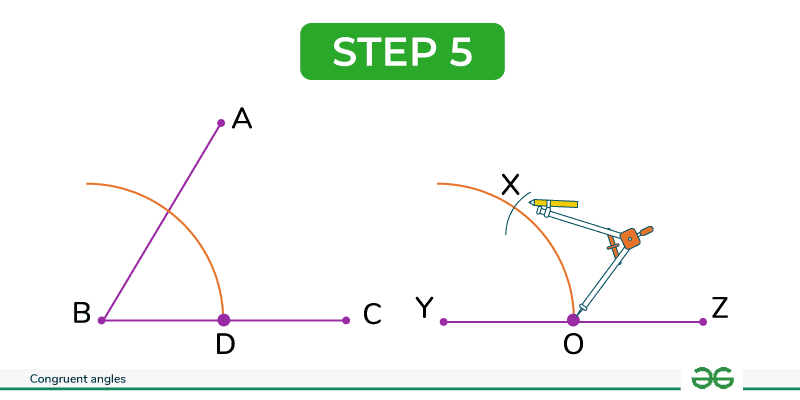
Step 6: Draw a line connecting points X and Y.

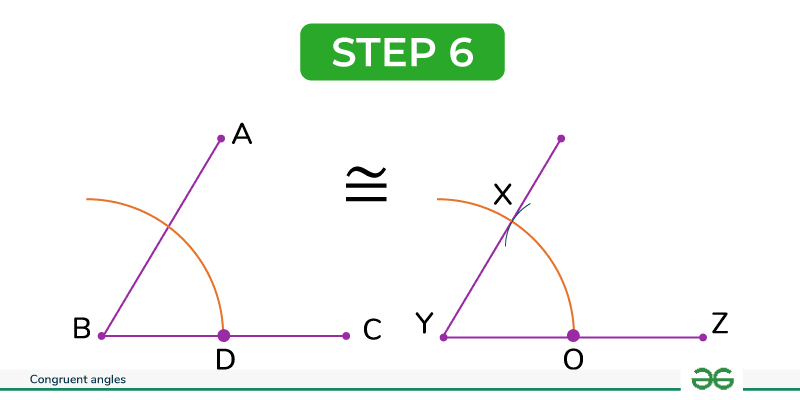
By following these steps, we obtain ∠ABC ≅ ∠XYZ, satisfying the definition of congruent angles. This construction demonstrates how to create an angle congruent to a given angle.

Congruent Angles Properties

Congruent angles have several properties:

• Equal Measure: Congruent angles have the same measure. In other words, they are equal in size.
• Symbol: Congruent angles are denoted by the symbol “≅”.
• Transitivity: If angle A is congruent to angle B, and angle B is congruent to angle C, then angle A is congruent to angle C. This property allows us to extend congruence relationships across multiple angles.
• Reflexivity: Any angle is congruent to itself. This means that angle A is congruent to angle A.
• Symmetry: If angle A is congruent to angle B, then angle B is congruent to angle A. Congruence is symmetric.

Congruent Angles Examples

Example 1: If two angles are ∠AOB and ∠PQR are congruent and value of ∠AOB = 80° and ∠PQR = x + 15°. Find the value of x.

Solution:

We know that congruent angles are equal.

Thus,

∠AOB = ∠PQR

x + 15 = 80

x = 80 – 15

x = 65°

Hence, value of x is 65°.

Example 1: If two angles are ∠LMN and ∠PQR are congruent and value of ∠LNM = 2x and ∠PQR is supplementary to 60°. Find the value of x.

Solution:

We know that congruent angles are equal.

Thus,

∠LMN = ∠PQR = 2x…{eq(i)}

∠PQR is supplementary to 60°

Then,

∠PQR + 60° = 180°

∠PQR = 180 – 60 = 120°

∠PQR = 2x = 120°…{from eq(i)}

x = 60°

Practice Questions on Congruent Angles

Q1: Find the value of ‘a’ if ∠LMN and ∠PQR are congruent and value of ∠LNM = 4a + 11 and ∠PQR = 91°.

Q2: Find the value of ‘a’ if ∠LMN and ∠PQR are congruent and value of ∠LNM = a – 5 and ∠PQR = 18°.

Q3: Find the value of ‘x’ if ∠LMN and ∠PQR are congruent and value of ∠LNM = x + 9 and ∠PQR = 91°.

Congruent Angles FAQs

What are congruent angles?

Congruent angles are angles that have the same measure. In other words, if two angles have the same size, they are considered congruent.

How do you find congruent angles?

We can find congruent angles by applying various geometric principles and theorems.

Do congruent angles add up to 180?

No, congruent angles do not necessarily add up to 180 degrees. Congruent angles have the same measure, but they may not be supplementary.

Which pairs of angles are congruent?

Pairs of angles that are congruent include:

• Vertical angles
• Corresponding angles in parallel lines
• Alternate interior and alternate exterior angles in parallel lines
• Same side interior angles formed by a transversal intersecting parallel lines
• Angles opposite equal sides in an isosceles triangle

What are conditions required for congruent angles?

One and only condition required for angles to be congruent is, they need to be equal in measurement.

Are right angles congruent?

Yes, Right angles are always congruent as they always measure 90°.

What is an example of a congruent angle pair?

Vertical angles are best examples of congruent angle pair.

Which geometrical shape has 3 congruent angles?

Equilateral triangle have three congruent angles.