Class 9 RD Sharma Solutions – Chapter 5 Factorisation of Algebraic Expressions- Exercise 5.2 | Set 2
Last Updated :
11 Feb, 2021
Factorize each of the following expressions:
Question 13. 8x2y3-x5
Solution:
⇒ x2((2y)3 – x3)
⇒ x2(2y-x)((2y)2+2xy+x2) [x3-y3=(x-y)(x2+xy+y2)]
⇒ x2(2y-x)(4y2+2xy+x2)
Therefore, 8x3y3-x5 = x2(2y-x)(4y2+2xy+x2)
Question 14. 1029 – 3x3
Solution:
⇒ 3 (343 – x3)
⇒ 3(73 – x3) [x3-y3=(x-y)(x2+xy+y2)]
⇒ 3 (7-x)(72+7x+x2)
Therefore, 1029 – 3x3 = 3 (7-x)(72+7x+x2)
Question 15. x6+y6
Solution:
⇒ (x2)3 + (y2)3
⇒ (x2+y2)((x2)2-(xy)2+(y2)2)
⇒ (x2+y2)(x4-x2y2+y4) [x3+y3=(x+y)(x2-xy+y2)]
Therefore, x6+y6 = (x2+y2)(x4-x2y2+y4)
Question 16. x3y3+1
Solution:
⇒ (xy)3 + 13
⇒(xy+1)((xy)2-xy+12) [x3+y3=(x+y)(x2-xy+y2)]
⇒ (xy+1) (x2y2 – xy +1)
Therefore, x3y3+1 = (xy+1) (x2y2 – xy +1)
Question 17. x4y4 – xy
Solution:
⇒ xy(x3y3 – 1)
⇒ xy ((xy)3 – 13) [x3-y3=(x-y)(x2+xy+y2)]
⇒ xy (xy -1)((xy)2 +xy +12)
⇒ xy (xy-1)(x2y2 + xy+1)
Therefore, x4y4 – xy = xy (xy-1)(x2y2 + xy+1)
Question 18. a12+b12
Solution:
⇒ (a4)3+(b4)3
⇒ (a4+b4)((a4)2-a4b4+(b4)2) [x3+y3=(x+y)(x2-xy+y2)]
⇒ (a4+b4)(a8-a4b4+b8)
Therefore, a12+b12 = (a4+b4)(a8-a4b4+b8)
Question 19. x3+6x2+12x+16
Solution:
⇒ x3+6x2+12x+8+8
⇒ x3+3*x2*2+3*x*22+23+8 [a3+3a2b+3ab2+b3 = (a+b)3]
⇒ (x+2)3+23
⇒ (x+2+2)((x+2)2-2(x+2)+22) [x3+y3=(x+y)(x2-xy+y2)]
⇒ (x+4)(x2+22+4x-2x-4+4)
⇒(x+4)(x2+4+2x) [(a+b)2=a2+b2+2ab]
Therefore, x3+6x2+12x+16 = (x+4)(x2+4+2x)
Question 20. a3+b3+a+b
Solution:
⇒ (a3+b3)+1(a+b)
⇒ (a+b)(a2-ab+b2)+1(a+b) [a3+b3 = (a+b)(a2-ab+b2)]
⇒ (a+b)(a2 -ab +b2 +1)
Therefore, a3+b3+a+b = (a+b)(a2 -ab +b2 +1)
Question 21. 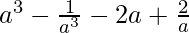
Solution:
⇒ 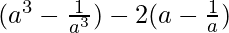
⇒ 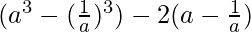
⇒ 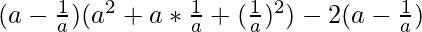
⇒ 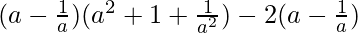
⇒ 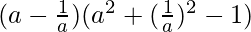
Therefore, 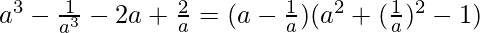
Question 22. 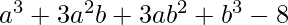
Solution:
⇒ (a+b)3-8 [a3+3a2b+3ab2+b3 = (a+b)3]
⇒ (a+b)3 – 23
⇒ (a+b-2) ((a+b)2+2(a+b)+22)
⇒(a+b-2)(a2+2ab+b2+2a+2b+4)
Therefore, a3+3a2b+3ab2+b3-8 = (a+b-2)(a2+2ab+b2+2a+2b+4)
Question 23. 8a3– b3 -4ax+2bx
Solution:
⇒ (2a)3 – b3 -2x(2a -b)
⇒ (2a-b)((2a)2 +2ab + b2) -2x(2a-b) [x3-y3=(x-y)(x2+xy+y2)]
⇒ (2a-b)(4a2 +2ab + b2-2x)
Therefore, 8a3-b3-4ax+2bx = (2a-b)(4a2 +2ab + b2-2x)
Question 24.
(i) 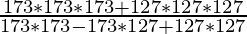
Solution:
⇒ 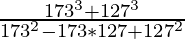
⇒ \frac{(173+127)(173^2-173*127+127^2)}{173^2-173*127+127^2} [a3+b3=(a+b)(a2+b2-ab)]
⇒ 173+127
⇒ 300
(ii) 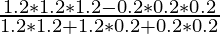
Solution:
⇒ \frac{1.2^3-0.2^3}{1.2^2+1.2*0.2+0.2^2} [a3-b3=(a-b)(a2+b2+ab)]
⇒ 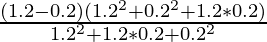
⇒ 1.2 – 0.2
⇒ 1.0
(iii) 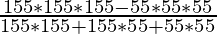
Solution:
⇒ \frac{153^3-55^3}{155^2+155*55+55^2} [a3-b3=(a-b)(a2+b2+ab)]
⇒ 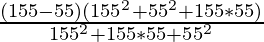
⇒ 155-55
⇒ 100
Share your thoughts in the comments
Please Login to comment...