Class 8 NCERT Solutions- Chapter 12 Exponents and Powers – Exercise 12.1
Last Updated :
10 Mar, 2021
Question 1. Evaluate:
Solution:
(i) 3–2
3-2 = 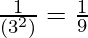 (Property used: a-n =
(Property used: a-n = 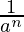 )
)
(ii) (– 4)– 2
(-4)-2 = 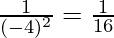 (Property used: a-n =
(Property used: a-n = 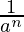 )
)
(iii) ( ) -5
) -5
( )-5 = (2)5 = 32 (Property used:
)-5 = (2)5 = 32 (Property used: 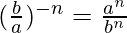 )
)
Question 2. Simplify and express the result in power notation with a positive exponent.
Solution:
(i) (-4)5 ÷ (-4)8
= (-4)5-8 = (-4) -3 (Property used: am ÷ an= am-n)
= 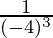
= 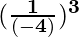
(ii) 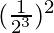
= 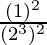 (Property used: (am)n = am×n)
(Property used: (am)n = am×n)
= 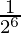
= 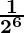
(iii) (-3)4 × (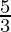 )4
)4
= ((3)4 × 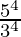 (Property used: (a/b)n = an/ bn & (-a)n = an if a is positive number and n is even)
(Property used: (a/b)n = an/ bn & (-a)n = an if a is positive number and n is even)
= 54
(iv) (3-7 ÷ 3-10) × 3-5
= 3 (-7-(-10)) × 3-5 (Property used: am ÷ an= am-n)
= 3 (-7+10) × 3-5
= 33 × 3-5
= 3 (3+(-5)) (Property used: am × an = a m + n)
= 3-2 (Property used: a-m =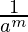 )
)
= 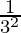
= 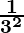
(v) 2-3 × (-7)-3
= (2 × (-7))-3 (Property used: am × bm = (a×b)m)
= (-14)-3 (Property used: a-m =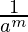 )
)
= 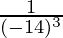
=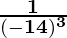
Question 3. Find the value of
Solution:
(i) (30 + 4-1) × 22
= (1 + (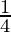 )) × 4 (a0 = 1 a ≠ 0)
)) × 4 (a0 = 1 a ≠ 0)
= (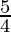 ) × 4
) × 4
= 5
(ii) (2-1 × 4-1) ÷ 2-2
= (2 × 4)-1 ÷ 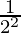 (Property used: am × bm = (a×b)m)
(Property used: am × bm = (a×b)m)
= (8)-1 ÷ 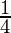
= (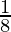 ) ÷
) ÷ 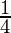
=(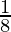 ) × 4
) × 4
= ( )
)
(iii) (1/2)-2 + (1/3)-2 + (1/4)-2
= 22 + 32 + 42 (Property used: 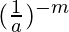 =am)
=am)
= 4 + 9 + 16
= 29
(iv) (3-1 + 4-1 + 5-1)0
= (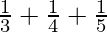 )0 (a0 = 1 (a ≠ 0)
)0 (a0 = 1 (a ≠ 0)
= 0
(v) {(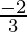 )-2}2
)-2}2
= (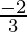 ) -2×2 (Property used: (am)n = am×n)
) -2×2 (Property used: (am)n = am×n)
= (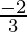 )-4 = (
)-4 = (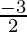 )4 (Property used: (b/a)-n = an/bn)
)4 (Property used: (b/a)-n = an/bn)
= 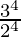
= 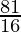
Question 4. Evaluate
Solution:
(i) (8-1 × 53) / 2-4
= (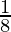 × 125) / (2-4) (Property used: (b/a)-n = an/bn)
× 125) / (2-4) (Property used: (b/a)-n = an/bn)
= (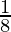 ) × 125 × 24
) × 125 × 24
= 250
(ii) (5-1 × 2-1) × 6-1
= (5 × 2)-1 × 6-1 (Property used: am × bm = (a×b)m)
= 10-1 × 6-1
= (10 × 6)-1 (Property used: am × bm = (a×b)m)
= 60-1
= 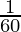
Question 5. Find the value of m for which 5m ÷ 5– 3 = 55
Solution:
5m-(– 3) = 55 (Property used: am ÷ an= am-n)
5m+3 = 55
m+3 = 5
m = 5-3
m = 2
Question 6. Evaluate
Solution:
(i) {(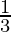 )-1 – (
)-1 – (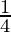 )-1}-1
)-1}-1
= (31 – 41) -1 (Property used: (1/a)-m = am)
= (-1)-1
= (1/(-1))1
= (-1)
(ii) (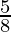 )-7 × (
)-7 × (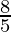 )-4
)-4
= (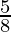 )7 × (
)7 × (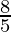 )-4 (Property used: (b/a)-n = (a/b)n)
)-4 (Property used: (b/a)-n = (a/b)n)
= (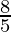 ) 7+ (-4) (Property used: am × an = a m + n)
) 7+ (-4) (Property used: am × an = a m + n)
= (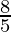 )3 = 83/53
)3 = 83/53
= 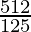
Question 7. Simplify
Solution:
(i) 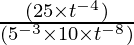 (t ≠ 0)
(t ≠ 0)
= 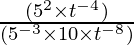 (Property used: am ÷ an= am-n ) (25 = 52)
(Property used: am ÷ an= am-n ) (25 = 52)
=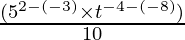
= 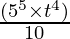
= 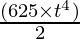
(ii) 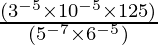
= 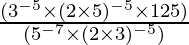
= 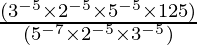 (Property used: (a×b)m = am × bm)
(Property used: (a×b)m = am × bm)
= (3-5-(-5) × 2-5-(-5) × 5 (-5)+3+7) (Property used: am ÷ an= am-n )
= (30 × 20 × 55) (a0 = 1 (a ≠ 0)
= 55
Share your thoughts in the comments
Please Login to comment...