Class 8 NCERT Solutions- Chapter 14 Factorisation – Exercise 14.3
Last Updated :
09 Mar, 2021
Question 1. Carry out the following divisions.
(i) 28x4 ÷ 56x
Solution:
28x4 = 2 × 2 ×7 × x × x × x × x
56x = 2 × 2 × 2 × 7 × x
28x4÷ 56x = 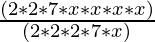 (grouping 28x to cancel)
(grouping 28x to cancel)
= ½ × x × x × x
= ½ x3
(ii) -36y3 ÷ 9y2
Solution:
-36y3 = -2 × 2 × 3 × 3 × y × y × y
9y2= 3 × 3 × y × y
-36y3 ÷ 9y2 = 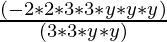 (grouping 9y2 to cancel)
(grouping 9y2 to cancel)
= -(2 × 2 × y)
= -4y
(iii) 66pq2r3 ÷ 11qr2
Solution:
66pq2r3 = 2 × 3 × 11 × p × q × q × r × r × r
11qr2 = 11 × q × r × r
66pq2r3 ÷ 11qr2 = 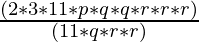 (grouping 11qr2 to cancel)
(grouping 11qr2 to cancel)
= (2 × 3 × p × q × r)
= 6pqr
(iv) 34x3y3z3 ÷ 51xy2z3
Solution:
34x3y3z3 = 2 × 17 × x × x × x × y × y × y × z × z × z
51xy2z3 = 3 × 17 × x × y × y × z × z × z
34x3y3z3 ÷ 51xy2z3 = 
= 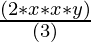 (grouping 17xy2z3 to cancel)
(grouping 17xy2z3 to cancel)
= 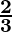 x2y
x2y
(v) 12a8b8 ÷ (-6a6b4)
Solution:
12a8b8 = 2 × 2 × 3 × a × a × a × a × a × a × a × a × b × b × b × b × b × b × b × b
-6a6b4 = -2 × 3 × a × a × a × a × a × a × b × b × b × b
12a8b8 ÷ (-6a6b4) = 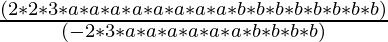
= – (2 × a × a × b × b × b × b) (grouping 6a6b4 to cancel)
= -2a2b4
Question 2. Divide the given polynomial by the given monomial.
(i) (5x2 – 6x) ÷ 3x
Solution:
5x2 – 6x = (5 × x × x) – (2 × 3 × x)
= 5x × (x) – 6 × (x)
= x(5x – 6)
3x = 3 × (x)
(5x2 – 6x) ÷ 3x = 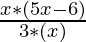 (grouping x to cancel)
(grouping x to cancel)
= 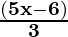
(ii) (3y8 – 4y6 + 5y4) ÷ y4
Solution:
3y8-4y6+5y4 = y4 [(3 × y × y × y × y) – (2× 2 × y × y) + (5)]
y4 = (y × y × y × y)
(3y8-4y6+5y4) ÷ y4 = 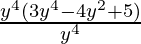 (grouping y4 to cancel)
(grouping y4 to cancel)
= (3x4-4y2+5 )
(iii) 8(x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2
Solution:
8 (x3y2z2 + x2y3z2 + x2y2z3 ) = 2 × 2 × 2 × x2y2z2 (x + y + z)
4 x x2y2z2 = 2 × 2 × x2y2z2
8(x3y2z2 + x2y3z2 + x2y2z3) ÷ 4x2y2z2 =  (grouping x2y2z2 to cancel)
(grouping x2y2z2 to cancel)
= 2(x+y+z)
(iv) (x3+2x2+3x) ÷ 2x
Solution:
x3+2x2+3x = x × (x2+2x+3 )
(x3+2x2+3x) ÷ 2x = 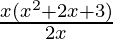 (grouping x to cancel)
(grouping x to cancel)
= 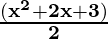
(v) (p3q6-p6q3) ÷ p3q3
Solution:
p3q6-p6q3 = p3q3(q3-p3)
(p3q6-p6q3) ÷ p3q3 = 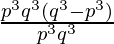 (grouping p3q3 to cancel)
(grouping p3q3 to cancel)
= q3– p3
Question 3. Work out the following divisions.
(i) (10x – 25) ÷ 5
Solution:
10x-25 = (5 × 2 × x) – (5 × 5)
= 5(2x-5)
(10x-25) ÷ 5 = 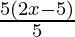 (grouping 5 to cancel)
(grouping 5 to cancel)
= (2x – 5)
(ii) (10x – 25) ÷ (2x – 5)
Solution:
10x-25 = 5(2x-5)
(10x-25)÷(2x-5) = 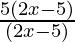 (grouping (2x-5) to cancel)
(grouping (2x-5) to cancel)
= 5
(iii) 10y(6y+21) ÷ 5(2y+7)
Solution:
10y(6y+21) = 5 × 2 × y × 3 × (2y+7)
10y(6y+21) ÷ 5(2y+7) = 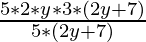 (grouping 5(2y+7) to cancel)
(grouping 5(2y+7) to cancel)
= 2 × 3 × y
= 6y
(iv) 9x2y2(3z-24) ÷ 27xy(z-8)
Solution:
9x2y2(3z-24) = 3 × 3 × x2 × y2 × 3 × (z-8)
27xy(z-8) = 3 × 3 × 3 × x × y × (z-8)
9x2y2(3z-24)÷27xy(z-8)= 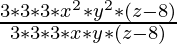 (grouping (27xy(z-8)) to cancel)
(grouping (27xy(z-8)) to cancel)
= xy
(v) 96abc(3a-12)(5b-30) ÷ 144 (a-4)(b-6)
Solution:
96abc(3a-12)(5b-30) = 2 × 2 × 2 × 2 × 2 × 3 × a × b × c × 3 × (a-4) × 5 × (b-6)
144(a-4)(b-6) = 2 × 2 × 2 × 2 × 3 × 3 × (a-4) × (b-6)
96abc(3a-12)(5b-30) ÷ 144(a-4)(b-6) = 
= (2 × 5 × a × b × c) (grouping (144(a-4)(b-6)) to cancel)
= 10abc
Question 4. Divide as directed.
(i) 5(2x+1)(3x+5) ÷ (2x+1)
Solution:
= 5(3x+1) (grouping (2x+1) to cancel)
(ii) 26xy(x+5)(y-4)÷13x(y-4)
Solution:
26xy(x+5)(y-4) = 2 × 13 × x × y × (x+5) × (y-4)
26xy(x+5)(y-4)÷13x(y-4) = 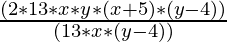 (grouping 13x(y-4) to cancel)
(grouping 13x(y-4) to cancel)
= (2 × y × (x+5))
= 2y(x+5)
(iii) 52pqr(p+q)(q+r)(r+p)÷104pq(q+r)(r+p)
Solution:
52pqr(p+q)(q+r)(r+p) = 13 × 2 × 2 × pqr(p+q)(q+r)(r+p)
104pq(q+r)(r+p) = 13 × 2 × 2 × 2 × pq(q+r)(r+p)
52pqr(p+q)(q+r)(r+p)÷104pq(q+r)(r+p) = 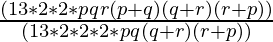
= 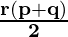 (grouping (52pq(q+r)(r+p)) to cancel)
(grouping (52pq(q+r)(r+p)) to cancel)
(iv) 20(y+4)(y2+5y+3)÷5(y+4)
Solution:
20(y+4)(y2+5y+3) = 2 × 2 × 5 × (y+4) × (y2+5y+3)
20(y+4)(y2+5y+3)÷5(y+4) = 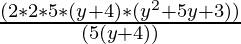 (grouping (5(y+4)) to cancel)
(grouping (5(y+4)) to cancel)
= 2 × 2 × (y2+5y+3)
= 4(y2+5y+3)
(v) x(x+1)(x+2)(x+3) ÷ x(x+1)
Solution:
= (x+2)(x+3) (grouping x(x+1) to cancel)
Question 5. Factorise the expressions and divide them as directed.
(i) (y2+7y+10) ÷ (y+5)
Solution:
(y2+7y+10) = (y2+5y+2y+10)
= (y(y+5) + 2(y+5)) (2 + 5 = 7 & 2 × 5 = 10)
= (y+5) (y+2)
(y2+7y+10) ÷ (y+5) = 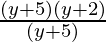 (grouping (y+5) to cancel)
(grouping (y+5) to cancel)
= (y+2)
(ii) (m2-14m-32)÷(m+2)
Solution:
(m2-14m-32) = (m2-16m+2m-32 )
= (m(m-16) + 2(m-16)) (-16 + 2 = -14 & -16 × 2 = -32)
= (m+2) (m-16)
(m2-14m-32)÷(m+2) = 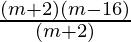 (grouping (m+2) to cancel)
(grouping (m+2) to cancel)
= (m-16)
(iii) (5p2-25p+20) ÷ (p-1)
Solution:
(5p2-25p+20) = (5p2-20p-5p+20)
=(5p(p-4)-5(p-4)) (-20 – 5 = -25 )
=(5p-5) (p-4)
=5 (p-1) (p-4)
(5p2-25p+20)÷(p-1) = 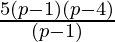 (grouping (p-1) to cancel)
(grouping (p-1) to cancel)
= 5(p-4)
(iv) 4yz(z2+6z-16)÷2y(z+8)
Solution:
4yz(z2+6z-16) = 2 × 2 × y × z × (z2+8z-2z-16)
= 2 × 2 × y × z × (z(z+8)-2(z+8)) (8 + (-2) = 6 & 8 × (-2) = -16)
= 2 × 2 × y × z × (z+8) (z-2))
4yz(z2+6z-16) ÷ 2y(z+8) = 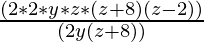 (grouping 2y(z+8) to cancel)
(grouping 2y(z+8) to cancel)
= 2 × z × (z-2)
= 2z(z-2)
(v) 5pq(p2-q2)÷2p(p+q)
Solution:
(p2-q2) = (p+q) (p-q) (IDENTITY a2-b2 = (a+b)(a-b) )
5pq(p2-q2)÷2p(p+q) = 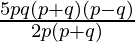 (grouping p(p+q) to cancel)
(grouping p(p+q) to cancel)
= 
(vi) 12xy(9x2-16y2) ÷ 4xy(3x+4y)
Soln.
12xy(9x2-16y2) = 2 × 2 × 3 × ((3x)2-(4y)2)
12xy(9x2-16y2) = 2 × 2 × 3 × (3x+4y) (3x-4y) (IDENTITY a2-b2 = (a+b)(a-b) )
12xy(9x2-16y2) ÷ 4xy(3x+4y) = 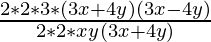 (grouping 4xy(3x+4y) to cancel)
(grouping 4xy(3x+4y) to cancel)
= 3 (3x-4y)
(vii) 39y3(50y2-98) ÷ 26y2(5y+7)
Solution:
39y3(50y2-98) = 3 × 13 × y3 × 2 × (25y2-49)
= 3 × 13 × y3 × 2 × ((5y)2-(7)2) (IDENTITY a2-b2 = (a+b)(a-b) )
= 3 × 13 × y3 × 2 × (5y+7) (5y-7)
26y2(5y+7) = 2 × 13 × y2 × (5y+7)
39y3(50y2-98)÷26y2(5y+7) = 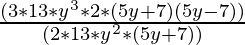 (grouping 26y2(5y+7) to cancel)
(grouping 26y2(5y+7) to cancel)
= (3 × y × (5y-7))
= 3y(5y-7)
Share your thoughts in the comments
Please Login to comment...